
proekcii_s_chislovymi_otmetkami
.pdf
|
|
В |
|
|
=1 |
|
|
C |
|
|
-Z |
|
C |
A |
|
Z |
|
|
|
|
А |
|
|
|
C` |
`В |
`А |
|
|
|
|
|
l |
|
L |
|
|
Н
Рис. 6
2.1.2. Взаимное положение прямых в пространстве
Параллельные прямые
Если прямые в пространстве параллельны, то параллельны их горизонтальные проекции (заложения), равны углы наклона к плоскости проекций (уклоны) и числовые отметки возрастают (или убывают) в одном направлении (рис.7).
A
D |
|
|
|
|
B |
|
|
|
С |
|
`A |
|
|
B` |
|
Н |
D` |
|
С` |
||
|
Рис. 7
11
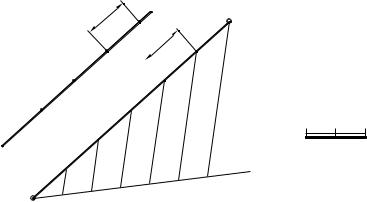
Задача. Через проекцию точки А (А4) провести прямую, параллельную прямой
CD (С2D8) (рис. 8).
l
5
A4
3
 4
4
 3
3
6 |
D |
8 |
|
|
|
|
l |
|
 7
7
 6
6
 5
5
0 1 2 М
С2
Рис. 8
Решение: Через точку А4 проводим прямую, параллельную проекции C2D8
отрезка CD.
Затем для определения интервала, проградуируем проекцию C2D8 прямой
CD (теорема Фалеса, рис 4).
На прямой, проведенной через точку А4 откладываем отрезки, равные интервалам на прямой CD и обозначаем их в нужном направлении.
Задача решена, все условия параллельности выполнены (проекции параллельны, интервалы l равны, числовые отметки возрастают в одном направлении).
Пересекающиеся прямые
Прямые в пространстве пересекаются, если пересекаются их проекции на плане, и в точке пересечения проекций прямые имеют одинаковые числовые отметки.
На рис. 9 изображены прямые, горизонтальные проекции (заложения)
которых пересекаются. Наша задача, определить кажущимся или действительным является пересечение прямых в точке Е≡F.
12

Для этого из проекций точек А3В7 к проекции (заложению) прямой АВ, а
так же из проекций точек С8Д3 к проекции (заложению) прямой СД восставляем перпендикуляры, на которых откладываем отметки (координаты Z) точек.
Полученные отрезки А0В0 и С0Д0, есть натуральная величина отрезков АВ и СД.
Определяем отметки точек Е и F. Отметка точки Е равна отрезку ЕЕ0, точки F-
отрезку FF0. Из сравнения отметок видно, что отметки точек Е (Е€АВ) и F (F€СД)
одинаковы (ЕЕ0=FF0), значит прямые пересекаются.
|
|
В0 |
|
|
Е0 |
|
С8 |
= |
|
В7 |
|
|
|
|
|
|
Е=F |
А0 |
|
Д3 |
|
|
|
|
|
= |
А3 |
|
Д0 |
С0 |
|
F0 |
|
|
0 1 2 3 М |
Рис.9
Скрещивающиеся прямые
Прямые в пространстве скрещиваются, если проекции этих прямых и числовые отметки их точек не удовлетворяют признакам параллельности и пересечения прямых.
Определим взаимное расположение прямых АВ и СД изображенных на рис.10. Для этого нужно решить, кажущимся или действительным является пересечение прямых в точке Е≡F. Предположим, что точки Е и F, принадлежащие соответственно прямым АВ и СД, являются конкурирующими. Построим натуральные величины отрезков АВ и СД. Для этого из проекций точек А3 В7 к
проекции (заложению) прямой АВ, а так же из проекций точек С3 Д4 к проекции
(заложению) прямой СД восставляем перпендикуляры, на которых откладываем
13

отметки (координаты Z) точек. Если необходимо, вертикальный масштаб может быть увеличен, по сравнению с горизонтальным масштабом. Полученные отрезки А0В0 и С0Д0, есть натуральная величина отрезков АВ и СД. Определяем отметки точек Е и F, для этого из мнимой точки пересечения (E=F) восставляем перпендикуляры (EE0=FF0). Из построения видно, что EE0≠FF0, следовательно,
точки E и F конкурирующие, а изображенные прямые – скрещивающиеся.
Отрезок EE0 FF0, следовательно, прямая СД выше АВ.
|
|
|
В0 |
|
С0 |
|
|
С3 |
|
Е0 |
В7 |
F |
0 |
|
|
|
|
||
|
|
|
|
|
|
Е=F |
Д0 |
|
|
|
Д4
А-3
0 |
0 1 2 3 М |
А |
|
|
Рис. 10 |
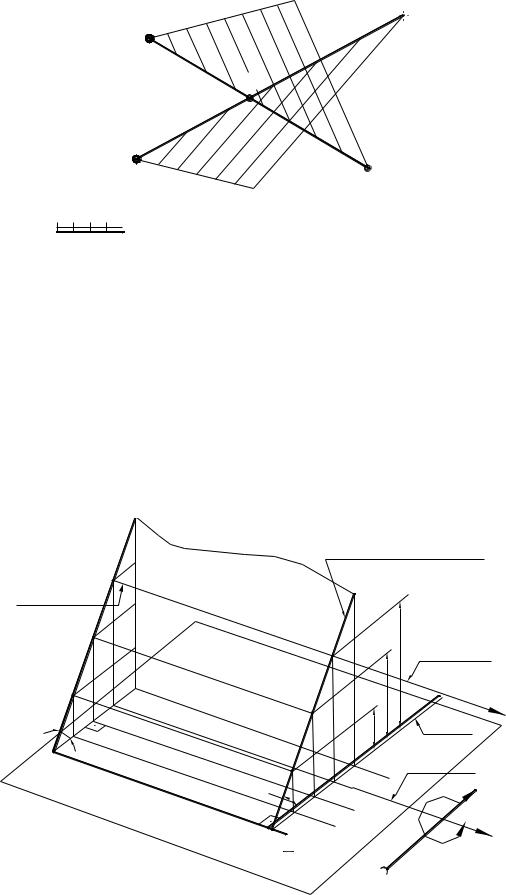
На рис. 11 изображены прямые АВ и СД, которые могут пересекаться или скрещиваться. Для того, чтобы определить это, находим отметки точек пересечения каждой прямой, проградуировав прямые (теорема Фалеса, рис.4). Из чертежа видим, что на отрезке АВ точка К имеет отметку 5,6м, а на отрезке СД - 6,5м. Прямые АВ и СД – скрещивающиеся, так как в точке пересечения проекций
(заложений) прямые имеют неодинаковые отметки.
14


 Д3
Д3
А2 3 |
4 |
|
5 |
||
4 |
5 К 6 |
|
|
||
7 |
6 |
|
8 |
7 |
|
8 |
||
|
||
|
9 |
|
С9 |
В10 |
|
|
0 1 2 3 М
Рис. 11.
2.2.Плоскость
Впроекциях с числовыми отметками плоскость может быть задана: прямой
иточкой вне ее, тремя точками, не лежащими на одной прямой, двумя пересекающимися прямыми, двумя параллельными прямыми, плоской фигурой.
Но наиболее удобным и наглядным изображением плоскости в проекциях с
числовыми отметками является задание с помощью масштаба уклона
плоскости (проградуированная линия ската).
|
3 |
Горизонталь |
|
плоскости |
|
2 |
|
1 |
|
|
|
Н |
|
0 |
|
|
|
|
Н |
линия ската
N
3 |
|
|
z=3 |
Направление |
|
|
|
|
простирания |
||
2 |
|
z=2 |
|
|
|
|
|
|
|
|
|
|
|
z=1 |
|
Масштаб |
|
|
|
|
уклонов |
|
|
1 |
|
N0 |
i |
|
|
|
|
Направлениепростирания |
|||
|
3 |
|
|||
|
|
|
|
С |
|
2 |
|
|
|
|
|
1 |
|
|
|
||
0 |
|
|
|
|
|
|
|
|
|
S0 |
|
M = M0 |
|
|
Ю |
||
|
|
|
|
||
Рис. 12
15
На рис.12 показана наклонная плоскость , которую лучше представить как плоский скат горы. Рассечем ее горизонтальными плоскостями по высоте через 1
м. Линии пересечения этих плоскостей с плоскостью будут горизонталями с отметками 0, 1, 2, 3 …..
Горизонталь плоскости - прямая, принадлежащая плоскости и
параллельная плоскости проекций Н.
Линия ската плоскости MN - прямая, принадлежащая плоскости и
перпендикулярная ее горизонталям.
Масштаб уклона плоскости (М0N0) - проградуированная проекция линии
наибольшего ската плоскости - MN.
Масштаб уклона плоскости перпендикулярен проекциям горизонталей,
изображается на чертеже двумя параллельными прямыми (тонкой и утолщенной)
и обозначается той же буквой, что и плоскость, с нижним индексом i. Отметки горизонталей указываются со стороны тонкой линии, вдоль масштаба уклона плоскости.
Угол падения φ0 - угол наклона плоскости (угол наклона линии ската) к
плоскости проекций Н.
Интервал плоскости - это расстояние между соседними горизонталями масштаба уклона i, соответствующее единице высотного превышения.
Направление простирания плоскости S0 - левое направление горизонталей, если наблюдатель смотрит вдоль линии ската плоскости в сторону ее спуска.
Угол простирания плоскости 0 - угол между направлением меридиана с юга на север и направлением простирания плоскости, который измеряется против часовой стрелки от северного конца меридиана.
16
2.3.Поверхность
Впроекциях с числовыми отметками поверхности задаются линейным каркасом. Линиями каркаса являются горизонтали поверхности - линии сечения поверхности горизонтальными плоскостями с числовыми отметками.
Многогранные поверхности изображаются вершинами с указанием их числовых отметок, горизонталями граней и градуированными проекциями ребер.
Кривые поверхности на плане задаются проекциями их горизонталей, а
также проекциями и числовыми отметками отдельных характерных точек поверхностей.
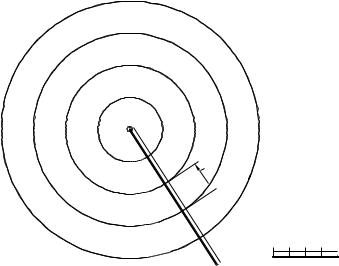
Возьмем, к примеру, прямой круговой конус с вертикальной осью (рис. 13).
Такая поверхность чаще всего задается проекцией его вершины S15 с указанием отметки и уклоном образующих (i = 1:2). Для того чтобы построить горизонтали данной поверхности, необходимо провести проекцию образующей SA,
проградуировать ее и провести горизонтали (окружности) с отметками,
соответствующими отметкам образующей.
S15
14
l=2
13  12 11
12 11

 A10
A10
0 1 2 3 М
Рис. 13
17
2.3.1. Топографическая поверхность
Топографическая поверхность (земная поверхность) задается дискретным
каркасом, который образуется ее горизонталями.
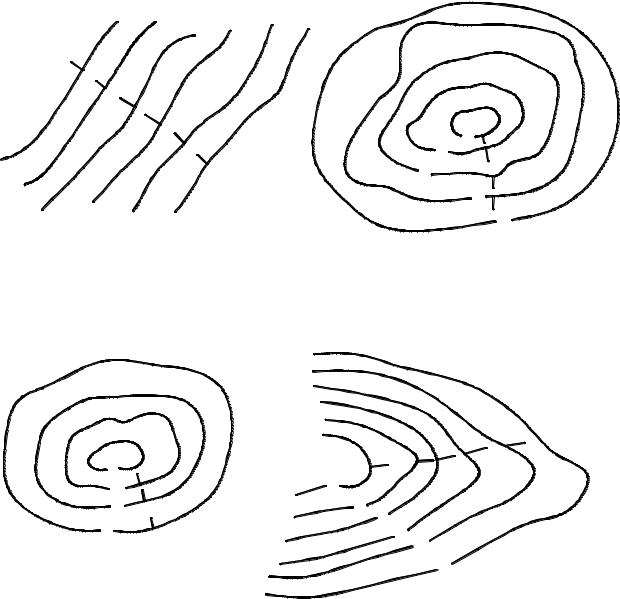
Для удобства определения характера топографической поверхности,
пользуются бергштрихами, которые проставляют перпендикулярно горизонтали и
направляют от нее в сторону спуска поверхности (рис. 14а, б, в, г).
а) |
|
|
|
б) |
20 |
21 |
23 |
24 |
25 |
|
|
|
||
|
|
22 |
|
|
|
20 |
|
19 |
|
18 |
|
17 |
|
16 |
местность с уклоном |
возвышение |
в) |
г) |
15 |
|
16 |
20 |
|
|
17 |
19 |
|
18 |
18 |
17 |
|
 16
16
 15
15
впадина |
хребет |
Рис. 14
18
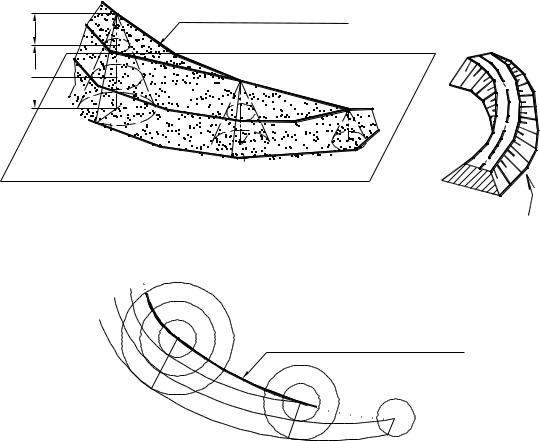
2.3.2. Поверхность равного уклона
При проектировании и строительстве автомобильных и железных дорог на криволинейных участках пути откосы насыпи выполняются в виде поверхности равного уклона.
Поверхность равного уклона - линейчатая поверхность, соприкасающаяся с множеством прямых круговых конусов с вертикальной осью, вершины которых расположены на заданной кривой - направляющей поверхности равного уклона.
Как и у всех ранее рассматриваемых поверхностей, у поверхности равного уклона есть свой определитель (рис15а, б):
Кривая линия - направляющая, прямой круговой конус с вертикальной
осью.
Конус перемещается в пространстве так, что его вершина остается на направляющей.
а)
С15
Направляющая кривая
1,0
1,0 1,0
H

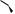

|
В14 |
Q |
А13 |

Откосы насыпи поверхности равного уклона
б)
14  13
13 
1 2
С15 |
Направляющая кривая |
В14








 А13
А13
Рис. 15
19

На рис. 15а показана в аксонометрии произвольная пространственная кривая АВС (направляющая). По этой кривой, как по направляющей,
перемещается |
вершина |
прямого кругового конуса, |
ось которого |
перпендикулярна |
плоскости |
Н, а образующие наклонены к этой плоскости под |
|
постоянным углом .
Поверхность Q, соприкасающаяся с конусом во всех его последовательных положениях, называется поверхностью равного уклона.
На рис.15б поверхность Q показана в ортогональной проекции.
Линия ската этой поверхности в каждой ее точке совпадает с образующей конуса, по которой в этой точке поверхность соприкасается с конусом.
Следовательно, угол наклона этой поверхности к плоскости проекций Н постоянен и равен углу наклона образующих конуса к плоскости Н, т.е. углу .
На чертеже поверхность равного уклона можно задать направляющей
(плоской или пространственной кривой) и уклоном i= tg к плоскости проекций Н.
3.РЕШЕНИЕ ПОЗИЦИОННЫХ ЗАДАЧ МЕТОДОМ ПРОЕКЦИЙ
СЧИСЛОВЫМИ ОТМЕТКАМИ
3.1.Пересечение плоскостей
Задача 1. Построить линию пересечения уклонов (рис. 16).
i  10
10
плоскостей , , заданных масштабами
i
9
8
Д9
10 9
8
7
6
7
6
С6
5
4
0 1 2 3

 М
М
Рис. 16
20
