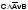Переведем числа из десятичной системы счисления в восьмеричную систему счисления.
Алгоритм перевода целых чисел из десятичной в восьмеричную систему счисления: Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
а) Число 22(10) перевести в восьмеричную систему счисления.
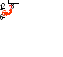
Ответ: 22(10) =26(2)
б) Число перевести 35,5625 (10) в восьмеричную систему счисления.
|
Перевод целой части |
Перевод дробной части |
|
|
|
Ответ: 35,5625 (10) =43,44(2)
Переведем числа из десятичной системы счисления в шестнадцатеричную систему счисления.
Алгоритм перевода целых чисел из десятичной в шестнадцатеричную систему счисления: Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
а) Число 22(10) перевести в шестнадцатеричную систему счисления.
Ответ: 22(10) =16(2)
б) Число перевести 35,5625 (10) в шестнадцатеричную систему счисления.
|
Перевод целой части |
Перевод дробной части |
|
|
|
Ответ: 35,5625 (10) =23,9(2)
Задание 2. Перевести данное число в десятичную систему счисления:
а) 100101101,1(2)
б)1056,48
в) 385,6416
Решение:
а) 100101101,1(2)? (10)
Алгоритм перевода чисел из двоичной системы счисления в десятичную систему счисления: Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики
100101101,1(2)=128+027+026+125+024+123+122+021+120+12-1= =256+32+8+4+1+0,5 =301, 5(10)
б)1056,4(8)?(10)
Алгоритм перевода чисел из восьмеричной системы счисления в десятичную систему счисления. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:
1056,4(8)=183+082+581+680+48-1=512+40+6+0, 5=550, 5(10)
в) 385,64(16)? (10)
Алгоритм перевода чисел из шестнадцатиричной системы счисления в десятичную систему счисления. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики
385,64(16)=3162+8161+5160+616-1+416-2= 768+128+5+0,375+0,015625 =901,390625 (10)
Ответ:
а) 100101101,1(2)= 301, 5(10)
б) 1056,4 (8)=558, 5 (10)
в) 385,64 (16)=901,390625 (10)
Задание 3 Сложите числа:
а) 101101110,1 (2) +1100100,11 (2);
б) 3015,1(8) +527,34(8).
Решение:
а) сложение двузначных чисел, действия выполняем по правилам двоичной арифметики:
а) 101101110,1 (2) +1100100,11 (2) =111010011,11 (2)
|
+ |
101101110,10 |
|
1100100,11 | |
|
|
111010011,01 |
Проверка: правильность вычислений проверим переводом исходных данных и результатов в десятичную систему счисления
101101110,1 (2) =128+027+126+125+024+123+122+121+020+12-1= 256+64+ +32+8+4+2+0,5 =366, 5(10)
1100100,11 (2) =126+125+024+023+122+021+020+12-1+12-2= 64+ 32+4+0,5+0,25=100,75(10)
366, 5(10)+ 100,75(10)= 467,25(10)
111010011,01 (2)= 128+127+126+025+124+023+022+121+120+02-1+12-2= 256+128+64+ 16+2+1+0,25 =467, 25(10)
б) сложение восьмеричных чисел действия выполняем по правилам восьмеричной арифметики, (см. приложении А таблицу 1).
3015,1(8) +527,34(8) =3544,44(8)
|
+ |
3015,10 |
|
527,34 | |
|
|
3544,44 |
Проверка: правильность вычислений проверим переводом исходных данных и результатов в десятичную систему счисления
3015,1(8) =383+082+181+580+18-1=1536+8+5+0, 5=1549, 125(10)
527,34(8) =582+281+780+38-1+48-2=320+16+7+0, 375+0,0625=343, 4375(10)
3544,44(8) =383+582+481+480+48-1+48-2=1536+320+4+0,5+0,0625= =1892,5625 (10)
1549, 125(10)+ 343, 4375(10) =1892,5625 (10)
Ответ: а) 111010011,11 (2)
б) 3544,44(8)
Задание 4 Выполните вычитание.
а) 101000010(2)-100000100(2);
б) 724,6(8)-365,14(8),
Решение:
а) вычитание двузначных чисел, действия выполняем по правилам двоичной арифметики
а) 101000010(2)-100000100(2)= 111110(2)
|
|
101000010 |
|
|
100000100 |
|
|
111110 |
б) вычитание восьмеричных чисел действия выполняем по правилам восьмеричной арифметики
724,6(8)-365,14(8) =337,44(8)
|
|
724,50 |
|
|
65,14 |
|
|
37,44 |
Ответ: а) 111110(2);
б) 337,44(8).
Задание 5. Выполните умножение.
а) 1001010(2)1001 (2);
б) 47,2(8) 64,14(8) =4000,270(8)
Решение:
а) Умножение двузначных чисел, действия выполняем по правилам двоичной арифметики
1001010(2)1001 (2)=1010011010 (2)
|
|
1001010 |
|
|
1001 |
| |
|
+ |
1001010 |
|
|
1001010 |
| |
|
|
1010011010 |
|
б) Умножение восьмеричных чисел действия выполняем по правилам восьмеричной арифметики (см. приложении А таблицу 2).
47,2(8) 64,14(8) =4000,270(8)
|
|
47,2 |
|
64,14 | |
|
+ + + |
2350 |
|
472 | |
|
2350 | |
|
3534 | |
|
|
4000,270 |
Ответ: a) 1001010(2)1001 (2)=1010011010 (2);
б) 47,2(8) 64,14(8) =4000,270(8)
Задание 6. Составить таблицу. Высказывания расчлените на простые и запишите символически, введя буквенные обозначения для простых их составляющих. Определите значения истинности высказываний:
«Если 12 делится на 6, то 12 делится на 3».
Решение:
Введем обозначение для простых высказываний:
A: 12 делится на 6;
B: 12 делится на 3.
Тогда высказывание «Если 12 делится на 6, то 12 делится на 3», можно записать символически AB.
|
A |
B |
AB |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
1 |
|
0 |
0 |
1 |
Т.е. высказывание-посылка «12 делится на 6» истинно и высказывание-следствие «12 делится на 3» истинно, то и составное высказывание по определению импликации истинно.
Ответ: Высказывание «Если 12 делится на 6, то 12 делится на 3», истинно.
Задание 6. Составить таблицу истинности для следующих формул и укажите, какие из этих формул являются выполнимыми, какие – опровержимыми, какие – тождественно истинными (тавтологиями), какие – тождественно ложными (противоречиями): ØA ( BC )
Решение:
Составить
таблицу истинности для логического
выражения:
|
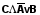
Переменные |
Промежуточные логические формулы |
Формула | ||||
|
A |
B |
C |
|
|
| |
|
0 |
0 |
0 |
1 |
0 |
0 | |
|
0 |
0 |
1 |
1 |
1 |
1 | |
|
0 |
1 |
0 |
1 |
0 |
1 | |
|
1 |
0 |
0 |
0 |
0 |
0 | |
|
1 |
1 |
0 |
0 |
0 |
1 | |
|
1 |
0 |
1 |
0 |
0 |
0 | |
|
0 |
1 |
1 |
1 |
1 |
1 | |
|
1 |
1 |
1 |
0 |
0 |
1 | |
Ответ:
Формула
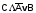в
некоторых случаях принимает значения
1, а в некоторых -0, то есть является
выполнимой.