8.3 Теоретические вопросы к защите расчетного задания № 8

1. В чем состоит разница в понятиях: «выборочная характеристика» и «теоретическая характеристика»?

2. Что такое точечная оценка параметра распределения?

3. Как определяется выборочная средняя?

4. Что характеризует выборочная средняя?

5. Как определяется выборочная дисперсия?

6. Что характеризует выборочная дисперсия?

7. Какие требования предъявляются к оценкам параметров?

8. Как определяется несмещенная статистическая оценка?

9. Что является несмещенной оценкой для: а) теоретической (генеральной) средней; б) теоретической (генеральной) дисперсии?

10. Как определяется состоятельная статистическая оценка?

11. Как определяется эффективная статистическая оценка?

12. В чем состоит разница в понятиях: «точечная оценка параметра» и «интервальная оценка параметра»?

13. Какая из оценок является более точной: точечная или интервальная?

14. Что называют доверительной вероятностью?

15. Что называют точностью оценки?

16. Влияет ли выбор доверительной вероятности на: а) точечную оценку; б) интервальную оценку?

17. Как изменится доверительный интервал для параметра распределения, если увеличить доверительную вероятность?

18. Как строится доверительный интервал для оценки математического ожидания нормально распределенного признака, если: а) теоретическая дисперсия известна; б) теоретическая дисперсия неизвестна?

9 Элементы теории корреляции

9.1 Теоретические сведения и примеры решения задач

Выборочный коэффициент корреляции:

,

где , выборочные средние Х и Y;

среднее значение величины ХY;

,  выборочные средние квадратические отклонения Х и Y.

Выборочное уравнение регрессии Y на X:

Выборочное уравнение регрессии X на Y:

Для оценки достоверности коэффициента корреляции проверяется гипотеза Н₀ об отсутствии линейной корреляционной связи между переменными в генеральной совокупности, т.е. Н₀: , по следующей схеме:

а) вычисляется статистика отклонения выборочного коэффициента корреляции от генерального коэффициента корреляции, гдеn – число наблюдений;

б) по таблице критических точек (двусторонней критической области) распределения Стьюдента (таблица А3 Приложения А) на уровне значимости и при числе степеней свободынаходится значение;

в) если не выполняется неравенство , гипотеза Н₀ отвергается, т.е. выборочный коэффициент корреляции существенно

отличается от нуля, что свидетельствует о достоверности коэффициента корреляции.

Задача. Для исследования зависимости объема производства (Y) от основных фондов (Х) получены статистические данные по 70 предприятиям за год.

Y	Х тыс. руб
	70	90	110	130	150	170	190
90	6
110	3	4	5
130		2	7	6
150			1	8	5
170			1	2	7	2
190						5
210							4
230							2

Предполагая, что между Х и Y существует линейная корреляционная зависимость, необходимо: а) определить коэффициент корреляции и сделать вывод о тесноте и направлении связи; б) оценить достоверность коэффициента корреляции на 5 %-ном уровне значимости; в) найти уравнения прямых регрессии.

Решение. Вычислим средние выборочные и:

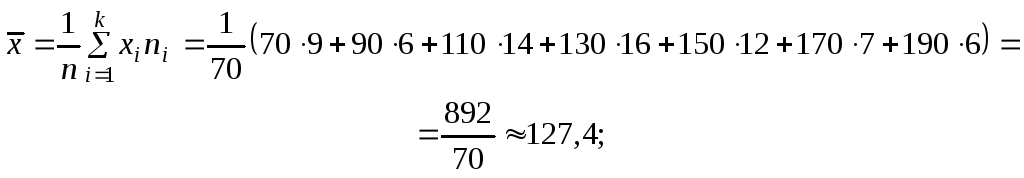
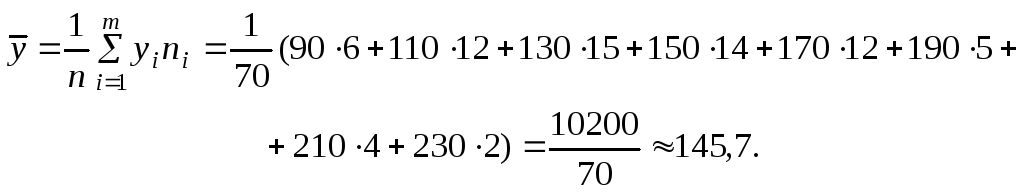
Найдем среднее значение величины ХY:

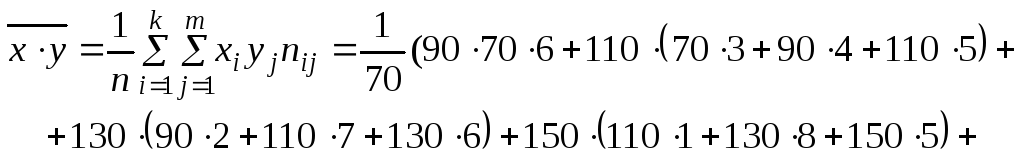
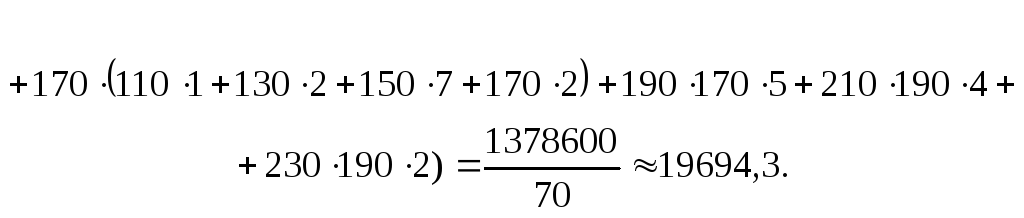
Вычислим дисперсии, а затем средние квадратические отклонения Х и Y:

.

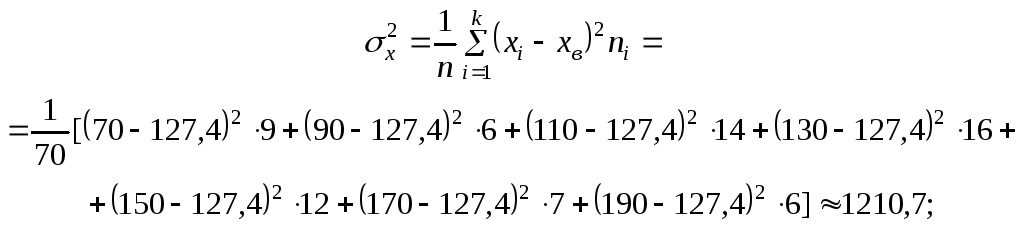
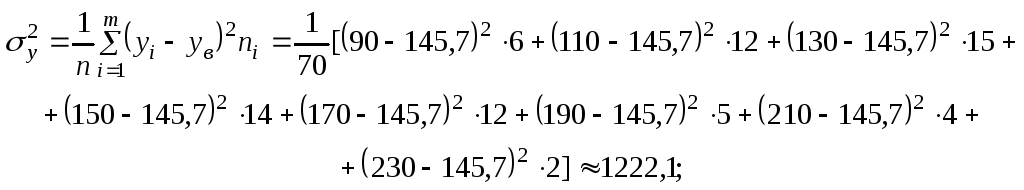
Вычислим выборочный коэффициент корреляции:

Полученное значение выборочного коэффициента корреляции показывает, что между переменными Х и Y существует достаточно тесная связь, близкая к линейной. Поскольку , то эта связь возрастающая, т.е. по мере увеличения основных фондов увеличивается объем производства.

Оценим достоверность коэффициента корреляции на 5%-ном уровне значимости. Для этого найдем статистику критерия по формуле :

Для уровня значимости и числа степеней свободыпо таблице А3 Приложения А находим критическое значение статистики. Поскольку, то коэффициент корреляции достоверен на 5%-ном уровне значимости.

Выборочное уравнение прямой регрессии Y на Х имеет вид:

Подставляя все найденные значения в последнее уравнение, получаем:

Аналогично найдем выборочное уравнение прямой регрессии Х на Y: