Физика
.docx|
|
При
движении материальной точки М ее
координаты Поэтому для задания закона движения м.т. необходимо указать либо вид функциональной зависимости всех трех ее координат от времени:
либо зависимость от времени радиус-вектора этой точки
Три скалярных уравнения (1.2) или эквивалентное им одно векторное уравнение (1.3) называются кинематическими уравнениями движения материальной точки.
|
||||||||||
|
|
Траектория – это линия, по которой движется тело (материальная точка). Траектория движения может быть прямой (тело перемещается в одном направлении) и криволинейной, то есть механическое движение может быть прямолинейным и криволинейным. Траектория прямолинейного движения в данной системе координат – это прямая линия. Например, можно считать, что траектория движения автомобиля по ровной дороге без поворотов является прямолинейной. Криволинейное движение – это движение тел по окружности, эллипсу, параболе или гиперболе. Пример криволинейного движения – движение точки на колесе движущегося автомобиля или движение автомобиля в повороте. Движение может быть сложным. Например, траектория движения тела в начале пути может быть прямолинейной, затем криволинейной. Например, автомобиль в начале пути движется по прямой дороге, а затем дорога начинает «петлять» и автомобиль начинает криволинейное движение. Путь – это длина траектории. Путь является скалярной величиной и в международной системе единиц СИ измеряется в метрах (м). Расчёт пути выполняется во многих задачах по физике. Некоторые примеры будут рассмотрены далее в этом учебнике.
Вектор перемещения Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением (рис. 1.1). Перемещение – величина векторная. Вектор перемещения направлен от начальной точки движения к конечной. Модуль вектора перемещения (то есть длина отрезка, который соединяет начальную и конечную точки движения) может быть равен пройденному пути или быть меньше пройденного пути. Но никогда модуль вектора перемещения не может быть больше пройденного пути. Модуль вектора перемещения равен пройденному пути, когда путь совпадает с траекторией (см. разделы Траектория и Путь), например, если из точки А в точку Б автомобиль перемещается по прямой дороге. Модуль вектора перемещения меньше пройденного пути, когда материальная точка движется по криволинейной траектории (рис. 1.1).
Ещё пример. Если автомобиль проедет по кругу один раз, то получится, что точка начала движения совпадёт с точкой конца движения и тогда вектор перемещения будет равен нулю, а пройденный путь будет равен длине окружности. Таким образом, путь и перемещение – это два разных понятия.
|
|
|
||||||||
|
|
В случае неравномерного движения важно знать, как быстро изменяется скорость с течением времени. Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является ускорение. Рассмотрим плоское движение, т.е. движение, при котором все участки траектории точки лежат в одной плоскости. Пусть вектор v задает скорость точки А в момент времени t. За время Dt движущаяся точка перешла в положение В и приобрела скорость, отличную от v как по модулю, так и направлению и равную v1 =v + Dv. Перенесем вектор v1 в точку А и найдем Dv (рис. 4). Средним ускорением неравномерного движения в интервале от t до t + Dt называется векторная величина, равная отношению изменения скорости Dv к интервалу времени Dt
Мгновенным ускорением а (ускорением) материальной точки в момент времени t будет предел среднего ускорения:
Таким образом, ускорение a есть векторная величина, равная первой производной скорости по времени.
Разложим
вектор Dv на
две составляющие. Для этого из
точки А (рис.
4) по направлению скорости v отложим
вектор Тангенциальная составляющая ускорения
т. е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю. Найдем вторую составляющую ускорения. Допустим, что точка В достаточно близка к точке А, поэтому Ds можно считать дугой окружности некоторого радиусаr, мало отличающейся от хорды АВ. Тогда из подобия треугольников АОВ и EAD следует Dvn/AB = v1/r, но так как AB = vDt, то
В
пределе при
Поскольку
называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны (поэтому ее называют также центростремительным ускорением). Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих (рис.5):
Итак, тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории), анормальная составляющая ускорения — быстроту изменения скорости по направлению (направлена к центру кривизны траектории). В зависимости от тангенциальной и нормальной составляющих ускорения движение можно классифицировать следующим образом:
1)
2)
Если
начальный момент времени t1=0,
а начальная скорость v1=v0,
то, обозначив t2=t и v2=v, получим
Проинтегрировав эту формулу в пределах от нуля до произвольного момента времени t, найдем, что длина пути, пройденного точкой, в случае равнопеременного движения
3)
4)
5)
6)
7)
|
|
|
||||||||
|
|
Предположим,
что вращение тела вокруг неподвижной
оси задано уравнением
Отношение
приращения угла поворота который произошло это приращение, называется средней угловой скоростью
Переходя
к пределу при
Таким
образом, угловая
скорость тела в данный момент времени
равна первой производной от угла
поворота по времени.
Угловая скорость измеряется в
Зная
зависимость угловой скорости
Отношение приращения угловой скорости к приращению времени называется средним угловым ускорением.
Переходя
к пределу при
Итак, угловое ускорение равно второй производной от угла поворота по времени или первой производной от угловой скорости по времени. Угловое
ускорение
измеряется в
|
|
|
||||||||
|
|
Масса – это свойство тела, характеризующее его инертность. При одинаковом воздействии со стороны окружающих тел одно тело может быстро изменять свою скорость, а другое в тех же условиях – значительно медленнее. Принято говорить, что второе из этих двух тел обладает большей инертностью, или, другими словами, второе тело обладает большей массой. Если два тела взаимодействуют друг с другом, то в результате изменяется скорость обоих тел, т. е. в процессе взаимодействия оба тела приобретают ускорения. Отношение ускорений двух данных тел оказывается постоянным при любых воздействиях. В физике принято, что массы взаимодействующих тел обратно пропорциональны ускорениям, приобретаемым телами в результате их взаимодействия. Сила – это количественная мера взаимодействия тел. Сила является причиной изменения скорости тела. В механике Ньютона силы могут иметь различную физическую природу: сила трения, сила тяжести, упругая сила и т. д. Сила является векторной величиной. Векторная сумма всех сил, действующих на тело, называетсяравнодействующей силой. Для измерения сил необходимо установить эталон силы и способ сравнения других сил с этим эталоном.
В
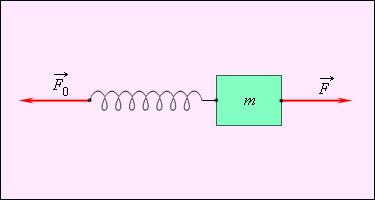
качестве эталона силы можно взять
пружину, растянутую до некоторой
заданной длины. Модуль силы F0,
с которой эта пружина при фиксированном
растяжении действует на прикрепленное
к ее концу тело, называют эталоном
силы.
Способ сравнения других сил с эталоном
состоит в следующем: если тело под
действием измеряемой силы
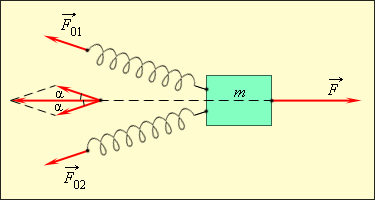
Если измеряемая сила F больше (по модулю) эталонной силы, то можно соединить две эталонные пружины параллельно (рис. 1.7.4). В этом случае измеряемая сила равна 2F0. Аналогично могут быть измерены силы 3F0, 4F0 и т. д.
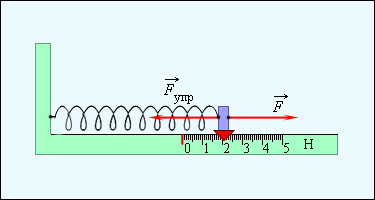
Измерение сил, меньших 2F0, может быть выполнено по схеме, показанной на рис. 1.7.5.
Эталонная сила в Международной системе единиц называется ньютон (Н). Сила в 1 Н сообщает телу массой 1 кг ускорение 1 м/с2 На практике нет необходимости все измеряемые силы сравнивать с эталоном. Для измерения сил используют пружины, откалиброванные описанным выше способом. Такие откалиброванные пружины называются динамометрами. Сила измеряется по растяжению динамометра (рис. 1.7.6).
Законы
механики Ньютона - три
закона, лежащие в основе т. н. классической
механики. Сформулированы И. Ньютоном
(1687). Первый закон: “Всякое тело
продолжает удерживаться в своём
состоянии покоя или равномерного и
прямолинейного движения, пока и
поскольку оно не понуждается приложенными
силами изменить это состояние”. Второй
закон: “Изменение количества движения
пропорционально приложенной движущей
силе и происходит по направлению той
прямой, по которой эта сила действует”.
Третий закон: “Действию всегда есть
равное и противоположное противодействие,
иначе, взаимодействия двух тел друг
на друга между собой равны и направлены
в противоположные стороны”.
1.1. Зако́н
ине́рции (Первый закон Нью́тона):
свободное тело, на которое не действуют
силы со стороны других тел, находится
в состоянии покоя или равномерного
прямолинейного движения (понятие
скорости здесь применяется к центру
масс тела в случае непоступательного
движения). Иными словами, телам
свойственна ине́рция (от лат. inertia —
“бездеятельность”, “косность”), то
есть явление сохранения скорости,
если внешние воздействия на них
скомпенсированы.
Системы
отсчёта, в которых выполняется закон
инерции, называются инерциальными
системами отсчёта (ИСО).
Впервые
закон инерции был сформулирован
Галилео Галилеем, который после
множества опытов заключил, что для
движения свободного тела с постоянной
скоростью не нужно какой-либо внешней
причины. До этого общепринятой была
иная точка зрения (восходящая к
Аристотелю): свободное тело находится
в состоянии покоя, а для движения с
постоянной скоростью необходимо
приложение постоянной силы.
Впоследствии
Ньютон сформулировал закон инерции
в качестве первого из трёх своих
знаменитых законов.
Принцип
относительности Галилея: во всех
инерциальных системах отсчета все
физические процессы протекают
одинаково. В системе отсчета, приведенной
в состояние покоя или равномерного
прямолинейного движения относительно
инерциальной системы отсчета (условно
— “покоящейся”) все процессы протекают
точно так же, как и в покоящейся
системе.
Следует
отметить что понятие инерциальной
системы отсчета — абстрактная модель
(некий идеальный объект рассматриваемый
вместо реального объекта. Примерами
абстрактной модели служат абсолютно
твердое тело или невесомая нить),
реальные системы отсчета всегда
связаны с каким-либо объектом и
соответствие реально наблюдаемого
движения тел в таких системах с
результатами расчетов будет
неполным.
1.2
Закон движения -
математическая формулировка того,
как движется тело или как происходит
движение более общего вида.
В
классической механике материальной
точки закон движения представляет
собой три зависимости трёх пространственных
координат от времени, либо зависимость
одной векторной величины (радиус-вектора)
от времени, вида
. |
|
|
||||||||
|
|
Импульсом называют векторную величину, равную произведению массы тела на ее скорость:
При взаимодействии тел замкнутой системы полный импульс системы остается неизменным:
Закон сохранения импульса есть следствие второго и третьего законов Ньютона. Пример использования закона сохранения импульса. Рассмотрим неупругое столкновение, при котором выполняется закон сохранения импульса. Пусть при абсолютно неупругом столкновении двух тел их скорость будет общей после удара. Ее нужно определить. Напишем векторное уравнение, соответствующее закону сохранения импульса системы:
После проецирования векторов на выбранную ось получим скалярное уравнение, которое позволит определить искомую величину vобщ. Еще один пример - реактивное движение. Рассмотрим простейший случай этого движения, при котором происходит одномоментное взаимодействие - выстрел из винтовки. До выстрела скорости винтовки и пули были равны нулю. После выстрела они имели различные скорости. Если известна скорость пули, ее масса и масса ружья, можно определить скорость, которую приобрело ружье после выстрела:
Отсюда после проецирования векторов на выбранную ось получим:
|
|
|
||||||||
|
|
Закон движения центра масс. Воспользовавшись законом изменения импульса, получим закон движения центра масс: dP/dt = M∙dVc/dt = ΣFi Центр масс системы движется так же, как двигалась бы частица с массой, равной массе системы, под действием силы, равной векторной сумме всех внешних сил, действующих на входящие в систему частицы. В частности, центр масс замкнутой системы относительно произвольной ИСО движется равномерно прямолинейно или покоится. Изменение импульса центра масс происходит за счет внешних сил. Внутренние силы не влияют на характер его движения, если внешнее воздействие на систему постоянно и однородно. Например, во время салюта движение центра масс разорвавшегося пиротехнического снаряда в постоянном однородном поле силы тяжести происходит по параболе. Если внешнее воздействие изменяется, то на различные части системы начинают действовать разные силы и характер движения центра масс меняется. В качестве примера рассмотрим движение системы, состоящей из одного тела - снаряда. В случае падения одной из частей разорвавшегося в воздухе снаряда на землю в системе появится новая внешняя сила - сила реакции опоры. Характер движения центра масс системы (осколков снаряда) при этом изменится. Наличие внутренних сил в этом примере является необходимым условием изменения характера движения центра масс системы. Без этих сил, обусловивших распад снаряда на части, не произошло бы изменения траектории его движения вплоть до падения снаряда на землю.
|
|
|
||||||||
|
|
Силой трения называют силу, которая возникает при движении одного тела по поверхности другого. Она всегда направлена противоположно направлению движения. Сила трения прямо пропорциональна силе нормального давления на трущиеся поверхности и зависит от свойств этих поверхностей. Законы трения связаны с электромагнитным взаимодействием, которое существует между телами. Различают трение внешнее и внутреннее. Внешнее трение возникает при относительном перемещении двух соприкасающихся твердых тел (трение скольжения или трение покоя). Внутреннее трение наблюдается при относительном перемещении частей одного и того же сплошного тела (например, жидкость или газ). Различают сухое и жидкое (или вязкое) трение. Сухое трение возникает между поверхностями твердых тел в отсутствие смазки. Жидким (вязким) называется трение между твердым телом и жидкой или газообразной средой или ее слоями. Сухое трение, в свою очередь, подразделяется на трение скольжения и трение качения. Рассмотрим законы сухого трения (рис. 4.5).
Подействуем
на тело, лежащее на неподвижной
плоскости, внешней силой Установлено, что максимальная сила трения покоя не зависит от площади соприкосновения тел и приблизительно пропорциональна модулю силы нормального давления N:
μ0 – коэффициент трения покоя, зависящий от природы и состояния трущихся поверхностей. Когда модуль внешней силы, а следовательно, и модуль силы трения покоя превысит значение F0, тело начнет скользить по опоре – трение покоя Fтр.пок сменится трением скольжения Fск (рис. 4.6):
где μ – коэффициент трения скольжения. Трение качения возникает между шарообразным телом и поверхностью, по которой оно катится. Сила трения качения подчиняется тем же законам, что и сила трения скольжения, но коэффициент трения μ ; здесь значительно меньше. Подробнее рассмотрим силу трения скольжения на наклонной плоскости (рис. 4.7).
На
тело, находящееся на наклонной плоскости
с сухим трением, действуют три силы:
сила тяжести
Если
Fтр = μN = mg cosα, F = mg sinα. При α > αmax тело будет скатываться с ускорением a = g ( sinα - μ cosα ), Fск = ma = F - Fтр. Если дополнительная сила Fвн, направленная вдоль наклонной плоскости, приложена к телу, то критический угол αmax и ускорение тела будут зависеть от величины и направления этой внешней силы. |
|
|
||||||||
|
|
Энергия — универсальная мера различных форм движения и взаимодействия. С различными формами движения материи связывают различные формы энергии: механическую, тепловую, электромагнитную, ядерную и др. В одних явлениях форма движения материи не изменяется (например, горячее тело нагревает холодное), в других — переходит в иную форму (например, в результате трения механическое движение превращается в тепловое). Однако существенно, что во всех случаях энергия, отданная (в той иди иной форме) одним телом другому телу, равна энергии, полученной последним телом. Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы. Если тело движется прямолинейно и на него действует постоянная сила F, которая составляет некоторый угол a с направлением перемещения, то работа этой силы равна произведению проекции силы Fs на направление перемещения (Fs= Fcosa), умноженной на перемещение точки приложения силы:
В общем случае сила может изменяться как по модулю, так и по направлению, поэтому формулой (11.1) пользоваться нельзя. Если, однако, рассмотреть элементарное перемещение dr, то силу F можно считать постоянной, а движение точки ее приложения — прямолинейным. Элементарной работой силы F на перемещении dr называется скалярная величина
где a — угол между векторами F и dr; ds = |dr| — элементарный путь; Fs — проекция вектора F на вектор dr (рис. 13). Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути. Эта сумма приводится к интегралу
Для вычисления этого интеграла надо знать зависимость силы Fs, от пути s вдоль траектории 1—2. Пусть эта зависимость представлена графически (рис. 14), тогда искомая работа А определяется на графике площадью заштрихованной фигуры. Если, например, тело движется прямолинейно, сила F=const и a=const, то получим
где s — пройденный телом путь (см. также формулу (11.1)). Из формулы (11.1) следует, что при a < p/2 работа силы положительна, в этом случае составляющая Fs совпадает по направлению с вектором скорости движения v (см. рис. 13). Если a > p/2, то работа силы отрицательна. При a = p/2 (сила направлена перпендикулярно перемещению) работа силы равна нулю. Единица работы — джоуль (Дж): 1 Дж — работа, совершаемая силой 1 Н на пути 1 м (1 Дж=1 Н × м). Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности:
За время dt сила F совершает работу Fdr, и мощность, развиваемая этой силой, в данный момент времени
т. е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы; N — величина скалярная. Единица мощности — ватт (Вт): 1 Вт — мощность, при которой за время 1 с совершается работа 1 Дж (1 Вт = 1 Дж/с). Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:
Физическую величину называют потенциальной энергией тела в поле силы тяжести
|
|
|
||||||||
|
|
механи́ческая эне́ргия описывает сумму потенциальной и кинетической энергий, имеющихся в компонентах механической системы. Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу. ЗСЭвМ В изолированной системе тел положительная работа внутренних сил увеличивает кинетическую энергию и уменьшает потенциальную. Отрицательная работа, напротив, увеличивает потенциальную энергию и уменьшает кинетическую. Именно благодаря этому выполняется закон сохранения энергии. Снова обратимся к простой системе тел, состоящей из земного шара и поднятого над Землей тела, например камня. Камень падает под действием силы тяжести. Силу сопротивления воздуха учитывать не будем. Работа, совершаемая силой тяжести при перемещении камня из одной точки в другую, равна изменению (увеличению) кинетической энергии камня:
В то же время эта работа равна уменьшению потенциальной энергии:
Работа силы всемирного тяготения, действующей со стороны камня на Землю, практически равна нулю. Из-за большой массы Земли ее перемещением и изменением скорости можно пренебречь. Так как в формулах (6.24) и (6.25) левые части одинаковы, то равны и правые части:
Равенство (6.26) означает, что увеличение кинетической энергии системы равно убыли ее потенциальной энергии (или наоборот). Отсюда вытекает, что
или
Изменение суммы кинетической и потенциальной энергий системы равно нулю. Величину E, равную сумме кинетической и потенциальной энергий системы, называют механической энергией системы:
Так как изменение полной энергии системы в рассматриваемом случае согласно уравнению (6.27) равно нулю, то энергия остается постоянной:
Таким
образом, в
изолированной системе, в которой
действуют консервативные силы,
механическая энергия сохраняется.
В этом состоит закон
сохранения механической энергии.
Энергия не создается и не уничтожается,
а только превращается из одной формы
в другую: из кинетической в потенциальную
и наоборот.
Учитывая, что в рассматриваемом
конкретном случае
или
Это уравнение позволяет очень просто найти скорость камня v2 на любой высоте h2 над землей, если известна начальная скорость v1 камня на исходной высоте h1. Закон сохранения механической энергии (6.29) легко обобщается на случай любого числа тел и любых консервативных сил взаимодействия между ними. Под Eк нужно понимать сумму кинетических энергий всех тел, а под Еп - полную потенциальную энергию системы. Для системы, состоящей из тела массой m и пружины, закон сохранения механической энергии имеет вид
Полная механическая энергия системы равна сумме ее кинетической и потенциальной энергий. В изолированной системе, в которой действуют только консервативные силы, механическая энергия сохраняется.
|
|
|
||||||||
|
|
момент инерции тела I относительно произвольной оси равен сумме момента инерции этого тела I0 относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями.
Теорема
Гюйгенса — Штейнера: момент
инерции тела
|
|
|
||||||||
|
|
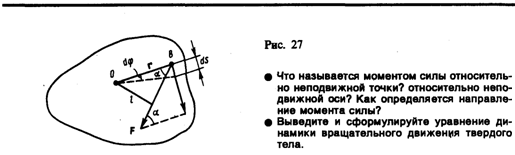
Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов). В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метров от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров до оси вращения. Более точно, момент силы частицы определяется как векторное произведение:
где
|
|
|
||||||||
|
|
Это и есть основное уравнение динамики вращательного движения твердого тела. Угловое ускорение ε и момент сил M в этом уравнении являются величинами алгебраическими. Обычно за положительное направление вращения принимают направление против часовой стрелки. момент инерции тела - I |
|
|
||||||||
|
|
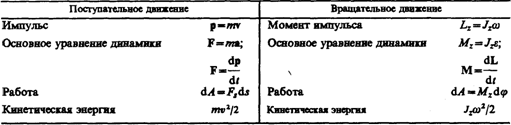
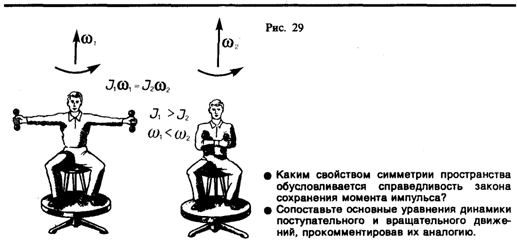
При сравнении законов вращательного и поступательного движений просматривается аналогия между ними, только во вращательном движении вместо силы «выступает» ее момент, роль массы «играет» момент инерции. Какая же величина будет аналогом импульса тела? Ею является момент импульса тела относительно оси. Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:
где r — радиус-вектор, проведенный из точки О в точку A, p=mv — импульс материальной точки (рис. 28); L — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к р. Модуль вектора момента импульса
где a — угол между векторами r и р, l — плечо вектора р относительно точки О. Моментом импульса относительно неподвижной оси z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса Lz не зависит от положения точки О на оси z.
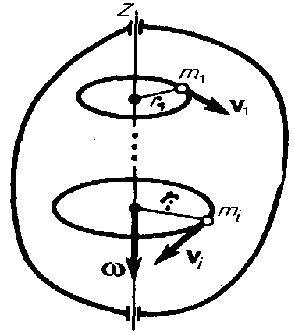
При вращении абсолютно твердого тела вокруг неподвижной оси z каждая отдельная точка тела движется по окружности постоянного радиуса ri с некоторой скоростью vi . Скорость vi и импульс mivi перпендикулярны этому радиусу, т. с. радиус является плечом вектора mivi . Поэтому можем записать, что момент импульса отдельной частицы равен
и направлен по оси в сторону, определяемую правилом правого винта. Монет импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:
Используя формулу (17.1) vi = wri, получим
т. е.
Таким образом, момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость. Продифференцируем уравнение (19.2) по времени:
т. е.
Это выражение — еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси.
Можно показать, что имеет место векторное равенство
В
замкнутой системе момент внешних
сил
Выражение (19.4) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени. Закон сохранения момента импульса — фундаментальный закон природы. Он связан со свойством симметрии пространства — его изотропностью, т. е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета (относительно поворота замкнутой системы в пространстве на любой угол). Продемонстрировать закон сохранения момента импульса можно с помощью скамьи Жуковского. Пусть человек, сидящий на скамье, которая без трения вращается вокруг вертикальной оси, и держащий в вытянутых руках гантели (рис. 29), приведен во вращение с угловой скоростью w1. Если человек прижмет гантели к себе, то момент инерции системы уменьшится. Поскольку момент внешних сил равен нулю, момент импульса системы сохраняется и угловая скорость вращения w2 возрастает. Аналогично, гимнаст во время прыжка через голову поджимает к туловищу руки и ноги, чтобы уменьшить свой момент инерции и увеличить тем самым угловую скорость вращения. Сопоставим основные величины и уравнения, определяющие вращение тела вокруг неподвижной оси и его поступательное движение (табл. 2). Таблица 2
|
|
|
||||||||
|
|
Класси́ческая
тео́рия тяготе́ния Ньюто́на (Зако́н
всео́бщего тяготе́ния Ньюто́на) —
закон, описывающий гравитационное
взаимодействие в
рамках классической
механики.
Этот закон был открыт Ньютоном в
1666 году. Он гласит, что сила гравитационного
притяжения между двумя материальными
точками массы
Здесь
|
|
|
||||||||
|
|
Молекулярная физика и термодинамика – две науки, дающие в совокупности полную картину изменений состояния вещества (обычно газообразного). Этот раздел физики занимается описанием • состояний вещества; • их изменений, то есть процессов. Фундаментальными понятиями термодинамики являются: состояние системыи процесс. Особенность данного раздела состоит в том, что он включает в себя 2 различных, но дополняющих друг друга, подхода к анализу и описанию состояния систем: термодинамический и молекулярно-кинетический. 2. История возникновения этого раздела, как и любого другого, началась с экспериментального наблюдения определенного круга физических явлений, установления свойственных этим явлениям закономерностей и оформления их в закон. Таким основополагающим законом явилась установленная Бойлем в 1661 г обратно пропорциональная зависимость давления Р в газе от занимаемого газом объема V, наблюдаемая при постоянной температуре газа T: P
С этого закона началась современная термодинамика, которая получила активное развитие в XIX в. прежде всего благодаря работамДжоуля. Параллельно термодинамике в XVIII-XIX вв. (Бернулли, Ломоносов , Авогадро) развивалась молекулярная физика, заклющающая в себе молекулярно-кинетическую теорию, способную объяснять и предсказывать термодинамическое состояние системы. 3. Основу молекулярной физики составляют следующие положения: 1) Модельные представления молекулярной физики: • все тела состоят из молекул • все молекулы находятся в постоянном хаотическом движении 2)
Состояние системы задается через
характеристики системы. 3) Частицы взаимодействуют по законам классической механики. 4) Для получения усредненных термодинамических параметров системы используются законы теории вероятности.
1) 2) дают макроскопические термодинамические параметрысистемыP, V , T , U ... 3) 4) 4. Термодинамика 1) Термодинамические равновесные (т.д.р.) параметрысистемызадают состояние системы. 2) Изменение параметров системызадает процесс, в котором участвует система. 3) Начала (законы) термодинамики определяют собой новое состояние системы. 1) 2) ⇒конечное состояние системы, т.е. P, V , T , U 3)
Шкалы: шкалах Цельсия (°С), Реомюра (°R) и Фаренгейта (°F), шкала Кельвина (К), абсолютная температурная шкала Ранкина (°Ra), Международная практическая температурная шкала (МПТШ) |
|
|
||||||||
|
|
17. Идеальный газ. Уравнение Менделеева-Клапейрона. |
|
|
||||||||
|
|
18. Газовые законы. Законы бойля-мариотта и гей-люссака. |
|
|
||||||||
|
|
19. Законы Авогадро и Дальтона . |
|
|
||||||||
|
|
20. Основные уравнения молекулярно-кинетической теории (МКТ - запомни эту аббревиатуру, это его любимый вопрос на экзамене). Этапы подтверждающие основные положения МКТ. |
|
|
||||||||



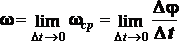 ;
;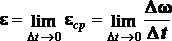 ;
;

 1.4.
Силы инерции
Законы
Ньютона, строго говоря, справедливы
только в инерциальных системах отсчета.
Если мы честно запишем уравнение
движения тела в неинерциальной системе
отсчета, то оно будет по виду отличаться
от второго закона Ньютона. Однако
часто, для упрощения рассмотрения,
вводят некую фиктивную “силу инерции”,
и тогда эти уравнения движения
переписываются в виде, очень похожем
на второй закон Ньютона. Математически
здесь всё корректно (правильно), но с
точки зрения физики новую фиктивную
силу нельзя рассматривать как нечто
реальное, как результат некоторого
реального взаимодействия. Ещё раз
подчеркнём: “сила инерции” — это
лишь удобная параметризация того, как
отличаются законы движения в инерциальной
и неинерциальной системах отсчета.
1.5.
Закон вязкости
Закон
вязкости (внутреннего трения) Ньютона
— математическое выражение, связывающее
напряжение внутреннего трения τ
(вязкость) и изменение скорости среды
v в пространстве
1.4.
Силы инерции
Законы
Ньютона, строго говоря, справедливы
только в инерциальных системах отсчета.
Если мы честно запишем уравнение
движения тела в неинерциальной системе
отсчета, то оно будет по виду отличаться
от второго закона Ньютона. Однако
часто, для упрощения рассмотрения,
вводят некую фиктивную “силу инерции”,
и тогда эти уравнения движения
переписываются в виде, очень похожем
на второй закон Ньютона. Математически
здесь всё корректно (правильно), но с
точки зрения физики новую фиктивную
силу нельзя рассматривать как нечто
реальное, как результат некоторого
реального взаимодействия. Ещё раз
подчеркнём: “сила инерции” — это
лишь удобная параметризация того, как
отличаются законы движения в инерциальной
и неинерциальной системах отсчета.
1.5.
Закон вязкости
Закон
вязкости (внутреннего трения) Ньютона
— математическое выражение, связывающее
напряжение внутреннего трения τ
(вязкость) и изменение скорости среды
v в пространстве
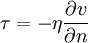 где
величина η называется коэффициентом
внутреннего трения или динамическим
коэффициентом вязкости (единица СГС
— пуаз). Кинематическим коэффициентом
вязкости называется величина μ = η / ρ
(единица СГС — Стокс, ρ − плотность
среды).
Закон
Ньютона может быть получен аналитически
приемами физической кинетики, где
вязкость рассматривается обычно
одновременно с теплопроводностью и
соответсвующим законом Фурье для
теплопроводности. В кинетической
теории газов коэффициент внутреннего
трения вычисляется по формуле
где
величина η называется коэффициентом
внутреннего трения или динамическим
коэффициентом вязкости (единица СГС
— пуаз). Кинематическим коэффициентом
вязкости называется величина μ = η / ρ
(единица СГС — Стокс, ρ − плотность
среды).
Закон
Ньютона может быть получен аналитически
приемами физической кинетики, где
вязкость рассматривается обычно
одновременно с теплопроводностью и
соответсвующим законом Фурье для
теплопроводности. В кинетической
теории газов коэффициент внутреннего
трения вычисляется по формуле
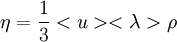 где
< u > — средняя скорость теплового
движения молекул, λ − средняя длина
свободного пробега.
где
< u > — средняя скорость теплового
движения молекул, λ − средняя длина
свободного пробега.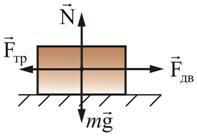 Рис.
4.5
Рис.
4.5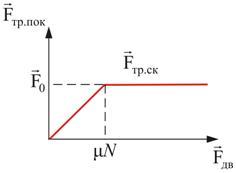 Рис.
4.6
Рис.
4.6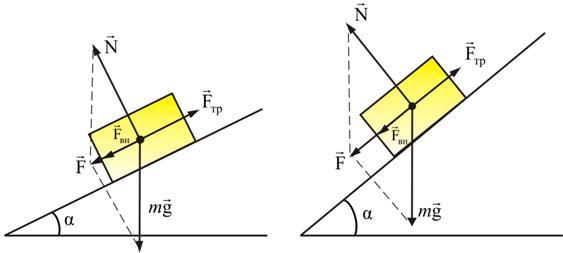 Рис.
4.7
Рис.
4.7



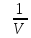 при
Т=const
при
Т=const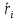 ,
,
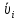 каждой молекулы – это микроскопические
каждой молекулы – это микроскопические