Глава 1. Политропные процессы.

До сих пор рассматривались процессы, у которых имелись вполне определенные признаки: изохорный процесс осуществлял­ся при постоянном объеме; изобарный — при постоянном давле­нии; изотермический — при постоянной температуре; адиабат­ный— при отсутствии теплообмена между рабочим телом и внеш­ней средой. Наряду с этими процессами можно представить еще бесконечное множество процессов, у которых имеются другие постоянные признаки.

Условились всякий процесс идеального газа, в котором удель­ная теплоемкость является постоянной величиной, называть политропным процессом, а линию процесса — политропой.

Из определения политропного процесса следует, что основные термодинамические процессы — изохорный, изобарный, изотерми­ческий и адиабатный,— если они протекают при постоянной удель­ной теплоемкости, являются частными случаями политропного процесса. Итак, политропный процесс проходит при постоянной теплоемкости.

Если теплоемкость зависит от температуры, то нужно найти среднюю теплоемкость, чтобы процесс стал политропным.

Уравнение процесса

Для исследования процесса и расчета слагаемых I закона термодинамики нужно установить связь между параметрами состояния в политропном процессе. Эта функция называется уравнением политропы. Запишем уравнение I закона термодинамики, преобразуем

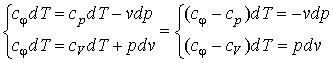
и поделим почленно

Так как  = const в процессе, то левая часть  = const и называется показатель политропы:

n = ,   

При этом, каждому значению n соответствует некоторый конкретный процесс.

Получили дифференциальное уравнение:

n=

Разделяем переменные

и интегрируем в пределах процесса

Потенцируем

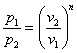  или   

Это выражение выполняется не только для крайних точек процесса, но и для всех промежуточных. Оно называется  уравнением политропы:

Запишем это уравнение через другие параметры P-T   и  V-T:

 

 

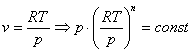
Теплоемкость политропных процессов

Теплоемкость политропного процесса  можно определить из выражения

 = n

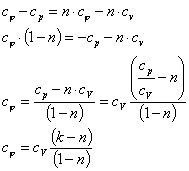
где k - показатель адиабаты.

Найдем значение   и  n  для изопроцессов определения  сведем результаты в таблицу

процесс		n
T=const		1
p=const		0
v=const
q=const	0	k

 

 

 

Изобразим зависимость (n) графически

 

 

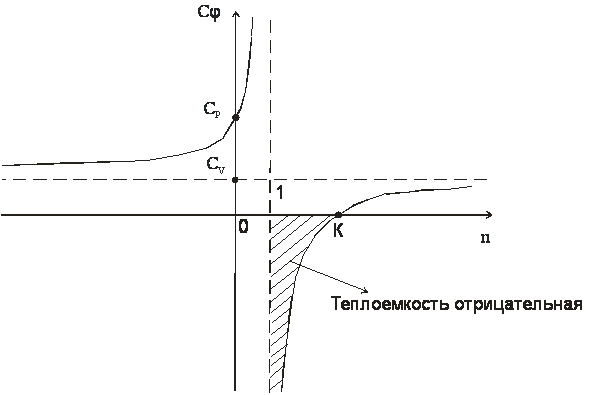
В деапазоне 1<n<k теплоемкость процессов отрицательная, т.е. с подводом теплоты температура системы уменьшается, а с отводом теплоты - увеличивается.

Смысл отрицательной теплоемкости заключается в том, что вся подведенная теплота расходуется на работу и, кроме этого, на работу затрачивается еще и часть внутренней энергии системы

 

dq=du+dl        подвод тепла

 

 

dq=du+dl      отвод тепла

 

 

Энергетические характеристики политропных процессов Изменение энтропии

По аналогии с интегралом работы было получено выражение для подсчета количества теплоты в ТДП. Для этого был введен параметр состояния системы – энтропия.

Энтропия является функцией состояния. Ее изменение в пределах процесса определяется как разность конечного и начального значений. Также как внутренняя энергия она определяется с точностью до произвольной постоянной. В ТДП нужно знать только ее изменение. Энтропия, и ее изменение не поддается физическому определению и измерению, а является расчетной величиной.
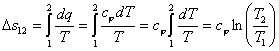