Раздел I

20. Из полной колоды карт (52 листа) извлекают сразу несколько карт. Сколько карт нужно извлечь для того, чтобы с вероятностью, большей чем 0,5, утверждать, что среди них будут содержаться карты одной и той же масти?

Решение.

Воспользуемся классической формулой вероятности

,

где m – число благоприятных исходов,

n – число всех исходов.

Обозначим искомое число через k. Прежде всего заметим, что если k > 4 , то среди выбранных карт наверняка найдутся карты одной и той же масти. Значит, нужно рассмотреть случаи, когда k = 2, 3, 4.

1. k = 2, число элементарных исходов равно .

Событие A = {две карты одной масти} есть сумма четырех несовместных событий: A = А1 + А2 + A3 + А4, где событию Ai (i = 1, 2, 3, 4) соответствует фиксированная масть. Так как (Выбираются любые две карты из 13 карт данной масти), то .

Тогда p(A) = 312/1326 = 0,235 < 0,5.

2. k = 3, . Найдем число исходов, входящих в событие .

Чтобы выбрать три карты разных мастей, нужно сначала выбрать три определенные масти из четырех. А затем выбрать по одной карте из тринадцати карт каждой из выбранных мастей.

Значит, .

Тогда , а вероятность события A = {есть карты одной масти} равна: p(A) = 13312/22100 = 0,602 > 0,5.

Ответ: нужно выбрать не меньше трех карт.

Раздел II

1. Игра проводится до выигрыша одним из двух игроков 2 партий подряд (ничью исключаются). Вероятность выигрыша партии каждым из игроков равна 0,5 и не зависит от исходов предыдущих партий. Найдите вероятность того, что игра окончится до 6 партии.

Решение.

p = 0,5 – вероятность выигрыша одним игроком

А - игра окончится до 6 партии

2. Ответ: вероятность того, что игра окончится до 6 партии, равна 0,406.

Раздел III

2. Имеются 2 урны. В первой 3 белых и 4 черных шара, во второй – 2 белых и 3 черных шара. Из первой урны наудачу перекладывают во вторую 2 шара, а затем из второй урны извлекают один шар. Он оказался белым. Какова вероятность того, что в первой урне осталось 2 белых и 3 черных шара?

Решение.

Воспользуемся формулой Байеса:

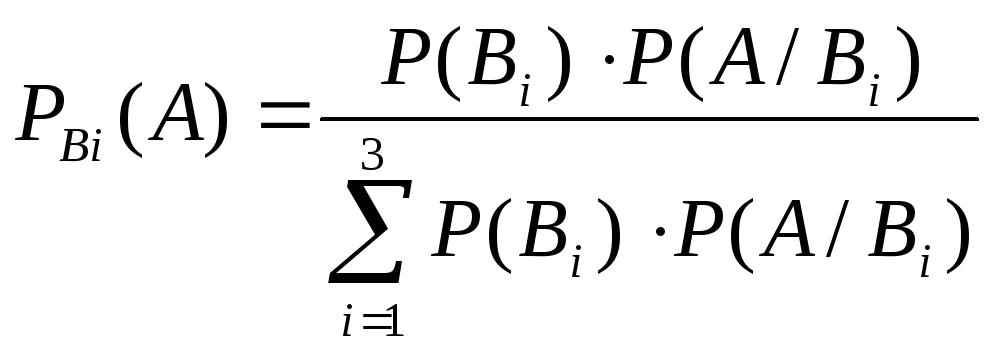
Существует 3 гипотезы:

В₁ – из первой урны переложили два белых шара,

В₂ – из первой урны переложили один белый и один черный шар,

В₃ – из первой урны переложили два черных шара,

Найдем вероятности гипотез:

; ;

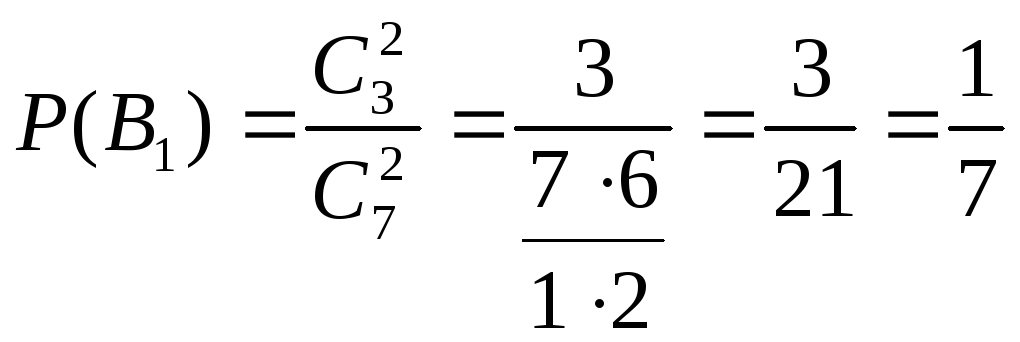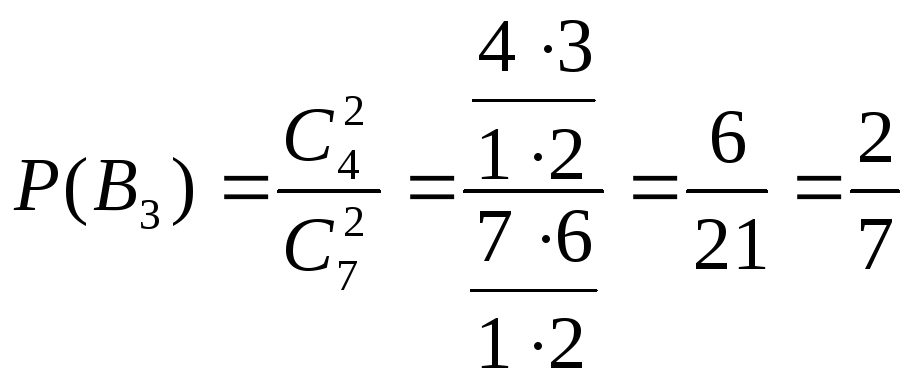
Найдем условные вероятности (шар, вынутый из 2-й урны, оказался белым): ; ;

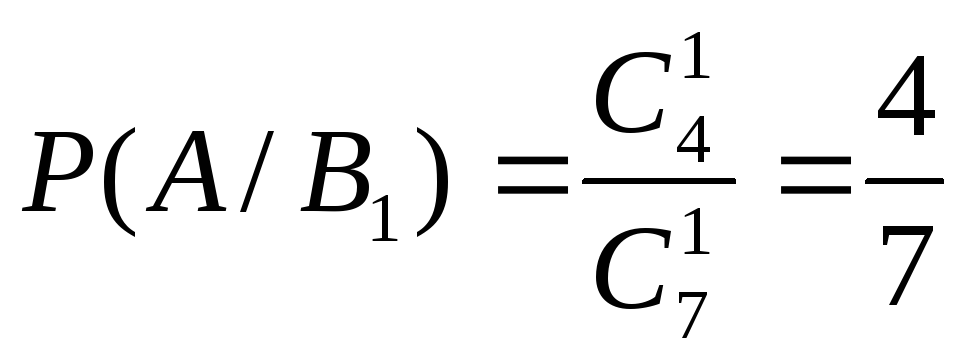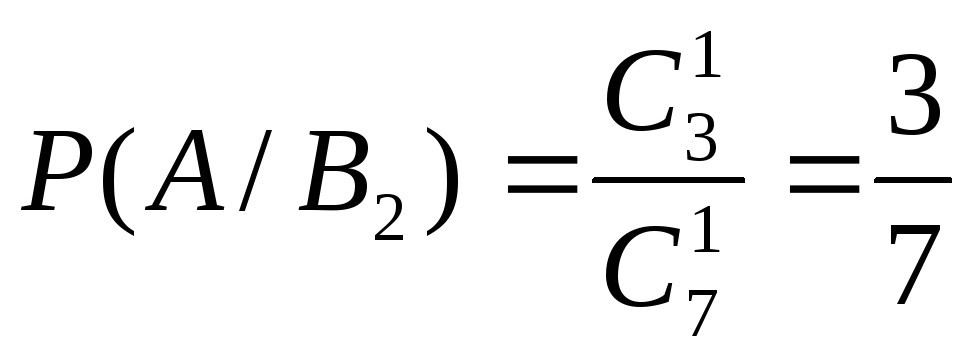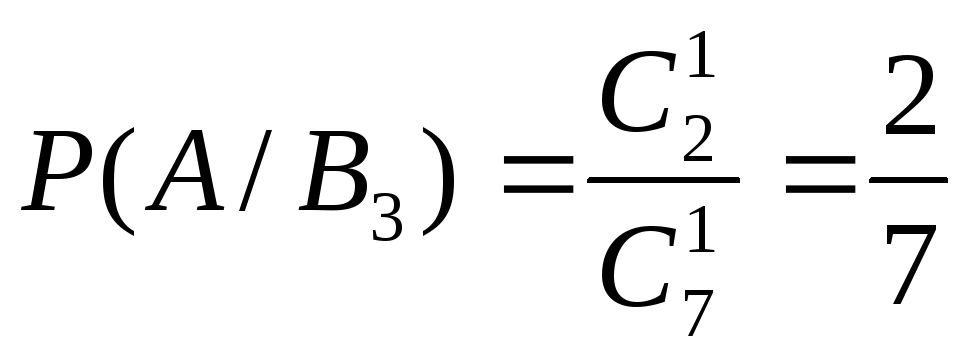
Чтобы в первой урне осталось 2 белых и 3 черных шара, из нее необходимо вытащить 1 белый и 1 черный шар (вторая гипотеза В₂):

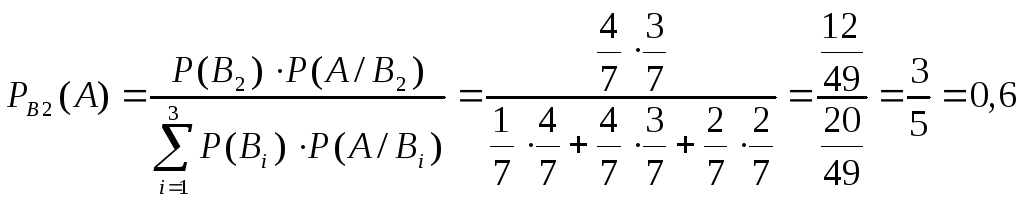
Ответ: вероятность того, что в первой урне осталось 2 белых и 3 черных шара, равна 0,6.

Раздел IV

3. Производится 4 независимых опыта, в каждом из которых событие А происходит с вероятностью 0,3. Событие В наступает с вероятностью 1, если событие А произошло не менее двух раз; не может наступить, если событие А не имело места, и наступает с вероятностью 0,6, если событие А имело место один раз. Найдите вероятность события В.

Решение.

Воспользуемся формулой полной вероятности:

А – выбранный стрелок попадет в цель.

Найдем вероятности гипотез:

В₁ – событие А не имело места,

В₂ – событие А произошло один раз,

В₃ – событие А произошло два раза,

В₄ – событие А произошло три раза,

В₅ – событие А произошло четыре раза.

Р(В₁) =

Р(В₂) =

Р(В₃) =

Р(В₄) =

Р(В₅) =

Проверка: Верно.

Найдем условные вероятности:

Вероятность того, что событие В наступит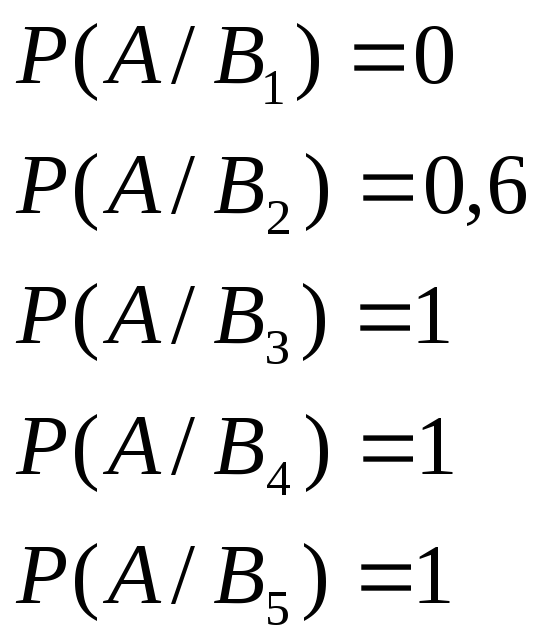

Ответ: вероятность того, что событие В наступит, равна 0,59526.