2. Сокращение линейных размеров движущихся предметов

:

(Лоренцево сокращение длины)

Стержень длинной l покоится в штрихованной системе координат и движется относительно не штрихованной системы координат, тогда K' l₀=x'₂-- x'₁, координаты стержня в штрихованной системе координат. х₁, х₂-- его координаты в нештрихованной системе координат. Длинна l=(x₂-- x₁), тогда из преобразований Лоренца следует:

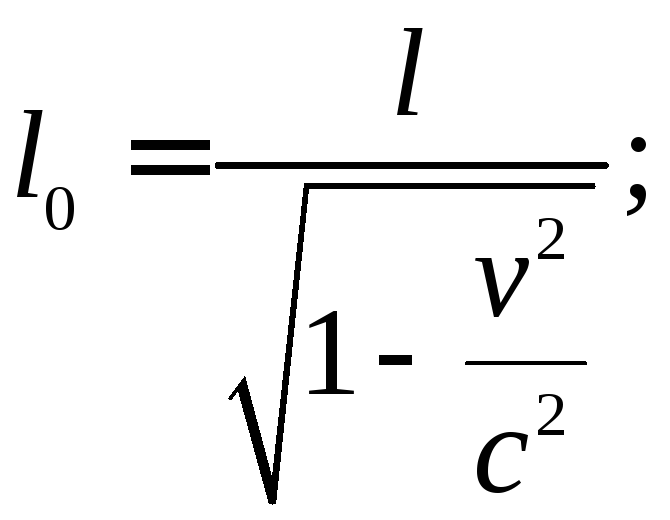
Релятивистский корень меньше единицы, т.к. v < c, следовательно:

l < l₀, т.е. длинна стержня относительно движущейся системы К меньше, чем длина того же стержня относительно системы отсчёта К', в которой стержень покоится, таким образом линейные размеры не являются инвариантными величинами, относительно различных инерциальных систем отсчёта. Связано это не со зрительным восприятием, а со свойствами пространства и времени. А формула Лоренца как раз и указывает на взаимосвязь пространства и времени между собой.

3. Собственное время: Пусть в инерциальной системе к' происходят два события в момент t'1 и t'2, тогда промежуток между этими событиями будет равен:

эти же два события в не штрихованной системе координат К, которая движется со скоростью v влево относительно К', происходят в моменты времени t₁и t₂.

==–==

Предположим, что оба события происходят в одной точке пространства:

х₁=х₂; x'₁=x'₂;

Время не является инвариантной величиной относительно различных инерциальных систем отсчёта. Чем быстрее движется инерциальная система отсчёта, тем быстрее течёт в ней время, относительно неподвижной инерциальной системы отсчёта. Таким образом время не абсолютно. Это следует из того, что выбор какая из двух систем К и К' движется, а какая покоится - произволен. Полученный нами факт совершенно не укладывается в обыденное понимание времени, эмоциональное восприятие времени нами.

Из полученного нами результата, следует что часы человека идущего пешком - идут быстрее, чем человека - летящего в самолёте. Это не иллюзия, а подтверждение того, что представление о пространстве и времени Ньютоновской механики, как абсолютных субстанциях, не верно.

4. Закон сложения скоростей:

Рассмотрим преобразования Лоренца:

===

Разделим числитель и знаменатель на тогда имеем:

==

Итак:

Аналогичные формулы получим в частных случаях движения системы координат вдоль Oy и Oz. В общем случае:

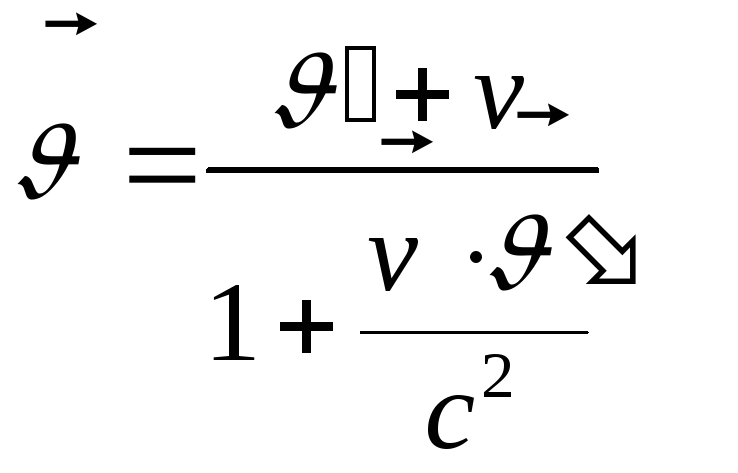
Эта формула также является косвенным доказательством строгой логичности специальной теории относительности. Действительно рассмотрим примеры.

1. Пусть K' относительно K движется cо скоростью с, тогда если само тело движется со скоростью v', то его скорость относительно К должна была бы быть равна (по Ньютону) v = v' + c, что противоречит постулату Эйнштейна

о пределности скорости света. Теперь из Релятивистской формулы.

==

2. Пусть материальная точка движется в штрихованной системе отсчёта со скоростью света, т. е. v' = c, сама же штрихованная система отсчёта, тоже движется относительно нештрихованной системе отсчёта К.

==

===

Формула Релятивистского сложения скоростей: ⁹⁶/₁₀₀ с < c, полученная из преобразований Лоренца подтверждается опытом Майкельсона - Морли, значит этот опыт является одним из подтверждений специальной теории относительности.