Колебания процесс, характеризующийся повторяемостью во времени и в пространстве, описывается периодической функцией:

f(t)=f(t+T_o)

Характерный признак – наличие в системе « гармонической или пропорциональной » силы направленной всегда к положению равновесия и пропорциональной смещению от положения равновесия и возвращающей осциллятор в положениюе равновесия

Гармонические - колебания происходящие по закону синуса или косинуса.

Пружинный маятник: А_X

X

m

Примеры осцилляторов: пружинный, математический и физический маятники

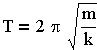
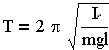
4.2. Дифференциальное уравнение гармонических колебаний и его решение.

Пусть в колебательной системе (осцилляторе) действует только гармоническая сила

F = ma,

a = dx²/dt² - ускорение материальной точки;

Разделив обе части последнего уравнения на , обозначив

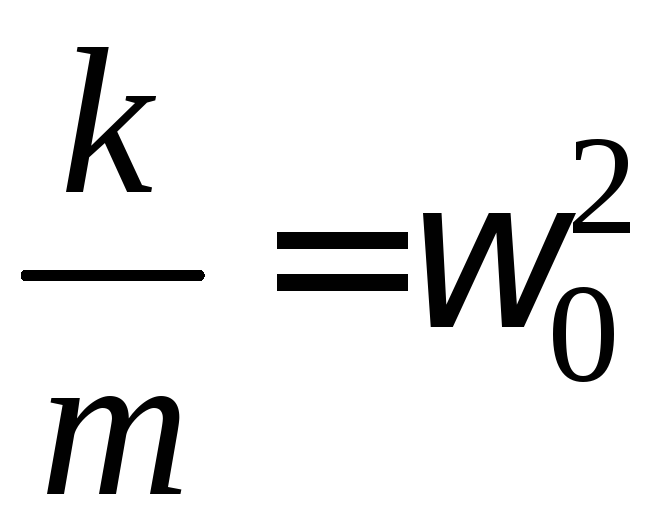
получим

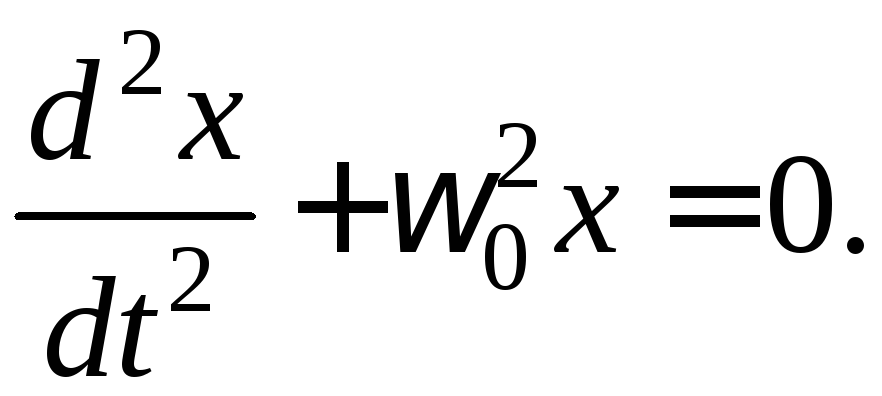
4.3

однородное дифференциальное уравнение второго порядка с постоянными коэффициентами.

Его решением является выражение вида:

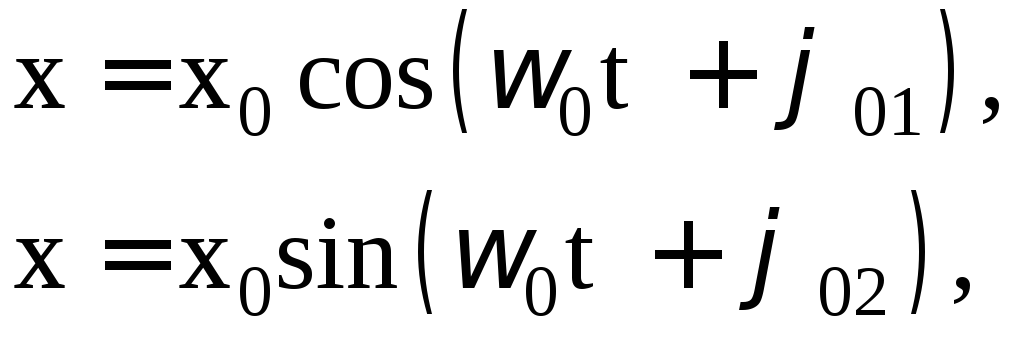
4.4

где x - смещение;

x₀ - амплитуда;

w₀ - собственная (круговая или циклическая) частота;

- начальная фаза.

фаза

4.4 Свободные (затухающие колебания). Дифференциальное уравнение затухающих колебаний и его решение. Характеристики затухающих колебаний.

В колебательной системе (осцилляторе) помимо силы упругости действует и сила сопротивления

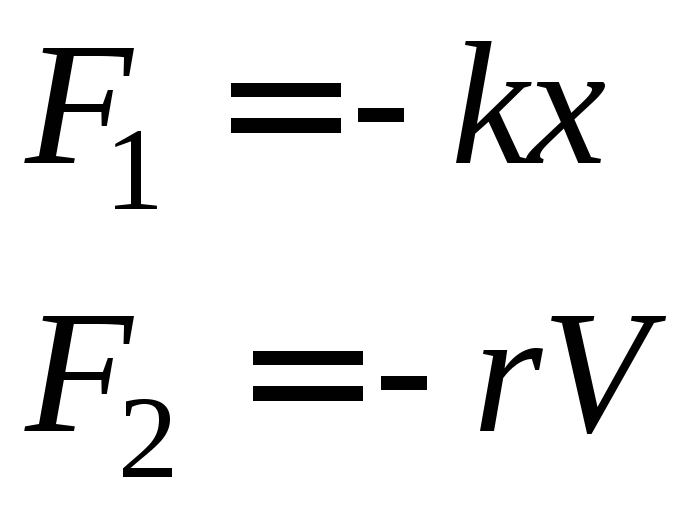
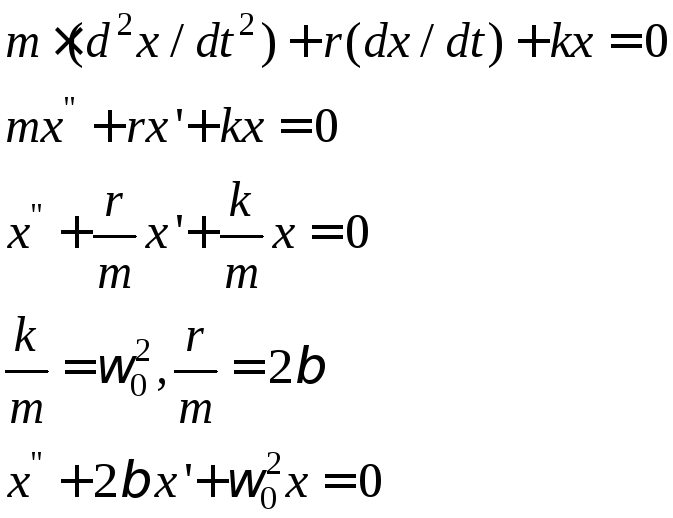
Однородное, линейное дифференциальное уравнение второго порядка с постоянными коэффициентами.

При его решение:

Где:

Физический смысл величин характеризующих затухание колебаний

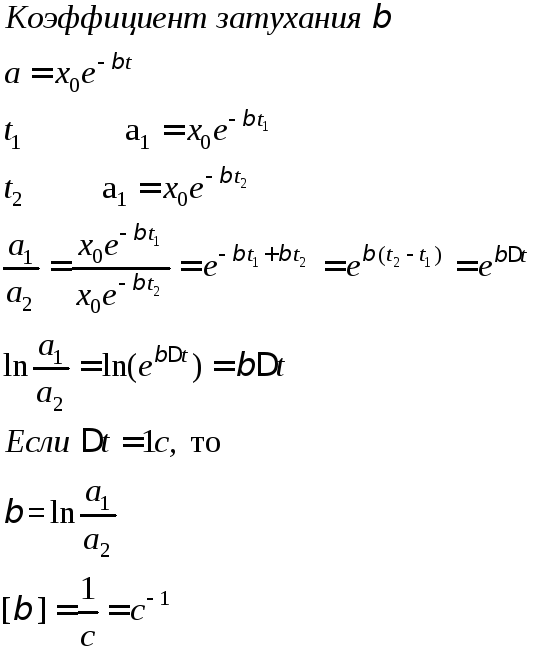
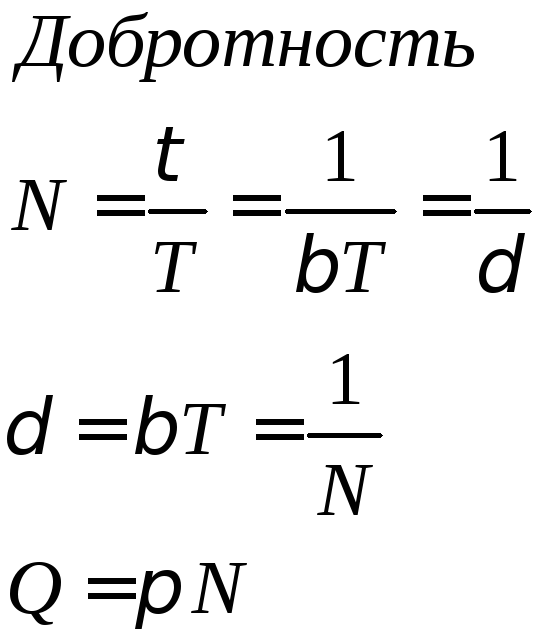
4.6. Вынужденные колебания гармонического осциллятора.

где F₀ - амплитудное значение действующей силы;

 - частота вынуждающей силы.

4

где F₁ - возвращающая сила, F = - kx;

F₂ - сила сопротивления, F = - rv (при малых значениях v);

F₃ - вынуждающая сила, F = F₀sint.

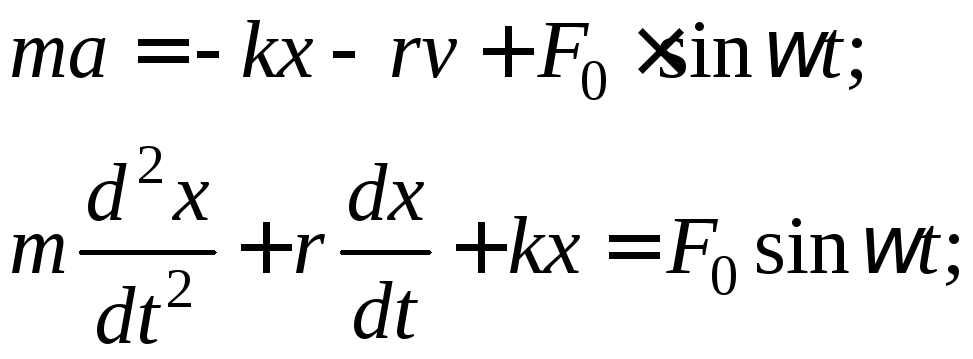
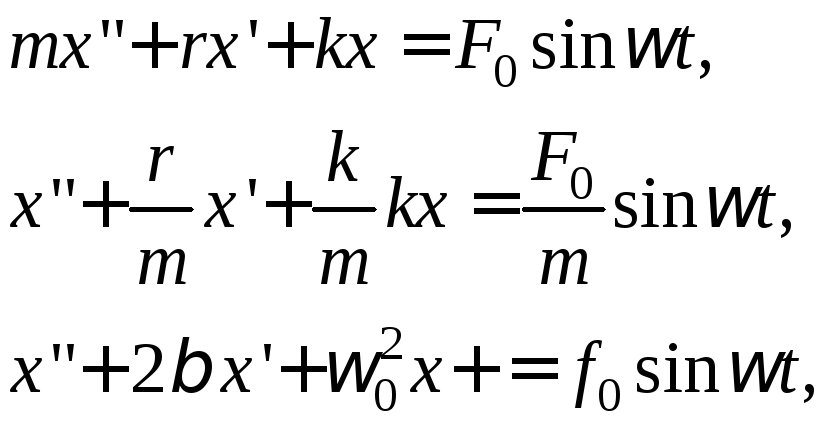
Неоднородное, линейное дифференциальное, второго порядка с постоянными коэффициентами.

Общее решение неоднородного уравнения равно сумме общего решения однородного и частного решения неоднородного.

ОН=ОО+ЧН

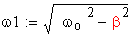
x_o и _o – постоянные, определяющиеся начальными условиями

Найдем частное решение неоднородного дифференциального уравнения по виду правой части:

x₂=a cos(t-)

a?

?

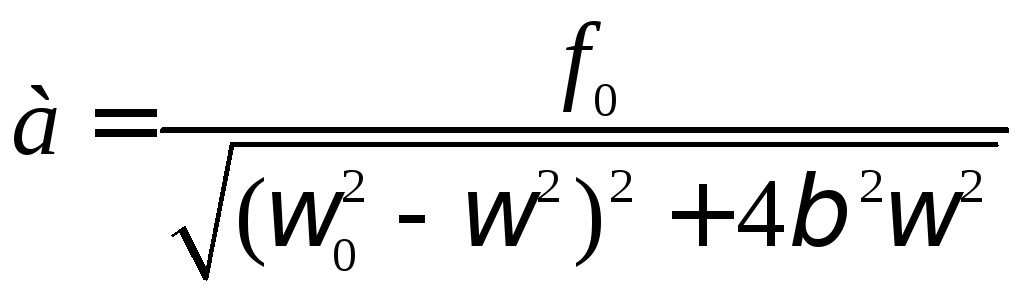
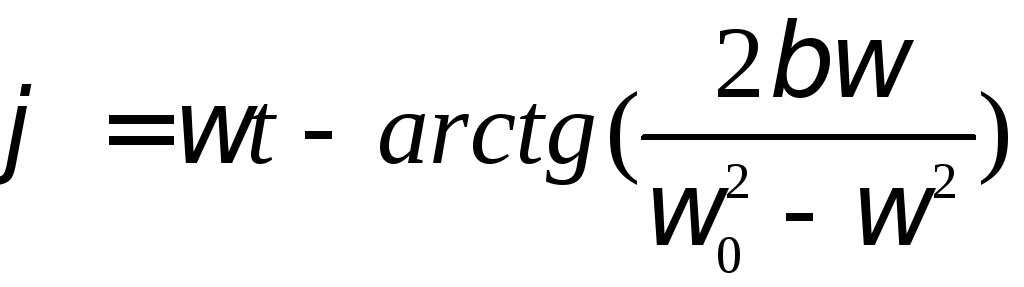
Частное решение неоднородного уравнения

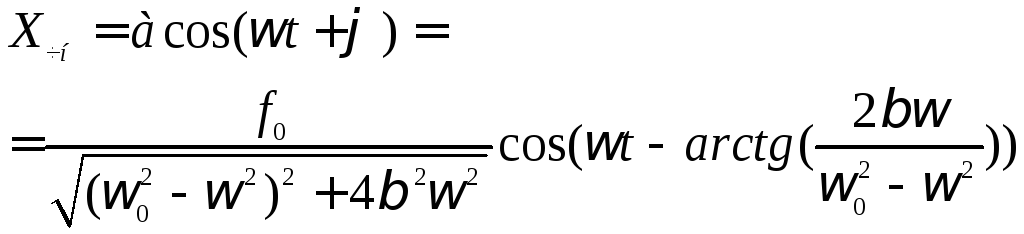
А его общее решение будет таким:

С течением времени t e^-t0 и первое слагаемое 0 и общее решение становится равным второму слагаемому – установившиеся колебания

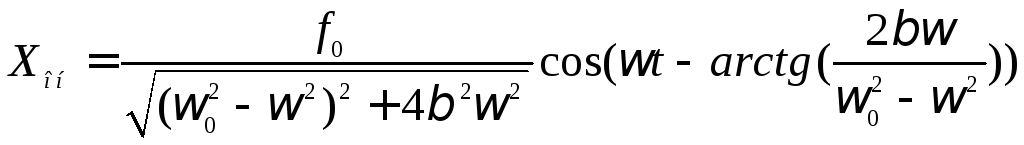
Анализ:

1. гармонические колебания происходят с частотой  равной частоте вынуждающей силы

2. амплитуда вынужденных колебаний зависит от амплитуды 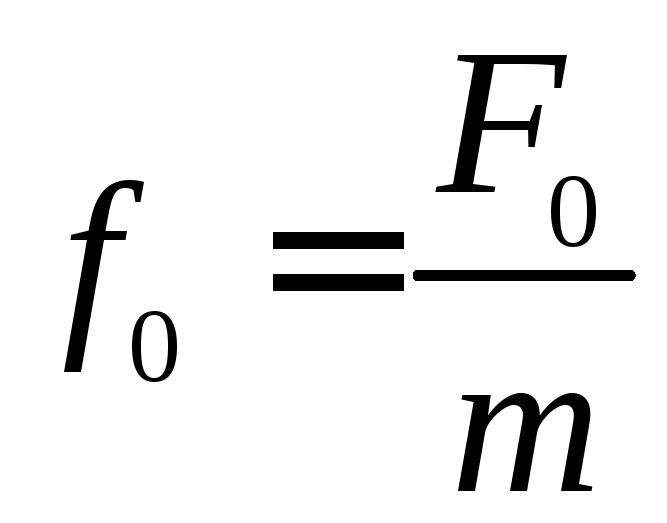вынуждающей силы,

3. параметров колебательной системы, свойств среды.

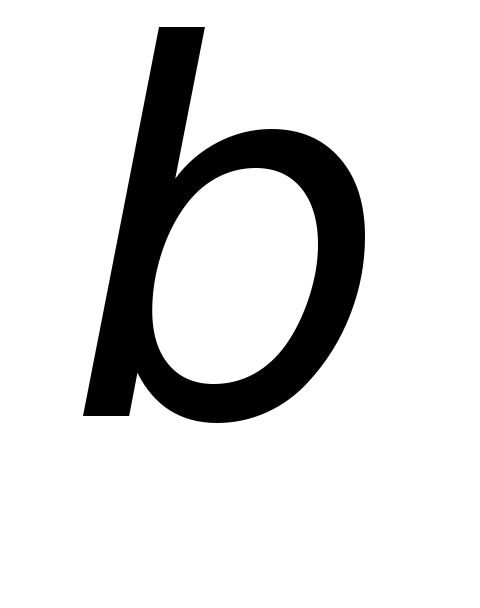4. и соотношение частот вынуждающей силы и собственной частоты

5. фаза вынужденных колебаний отстает от фазы вынуждающей силы на

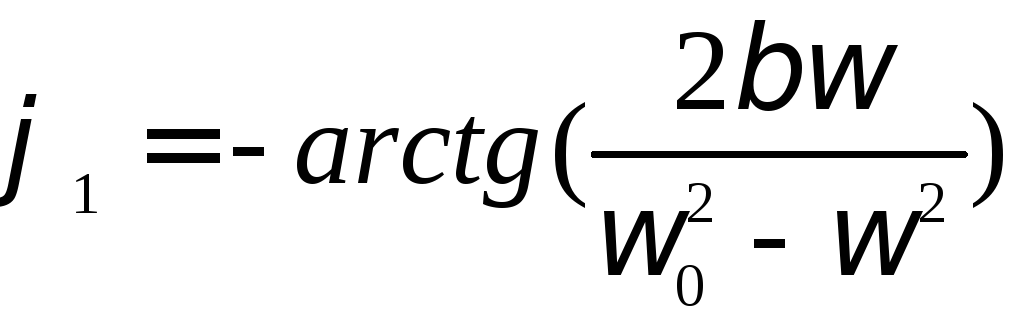
Резонанс

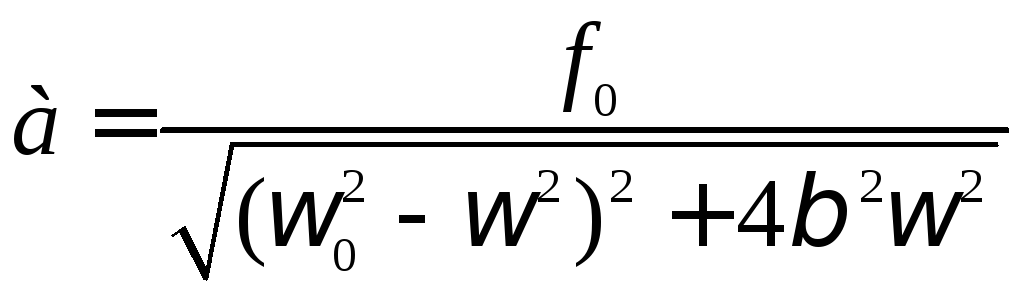
а=()

Анализируем знаменатель дроби на минимум:

((_о²-²)²+4²²)=2(_о²-²)2+4²2=

=4(_о²-²)+8²=0

4(_о²-² + 2²)=0;

=0 ²-(_o²-2²)=0;

=0 не имеет физического смысла

Нет смысла и у выражения

А вот выражение

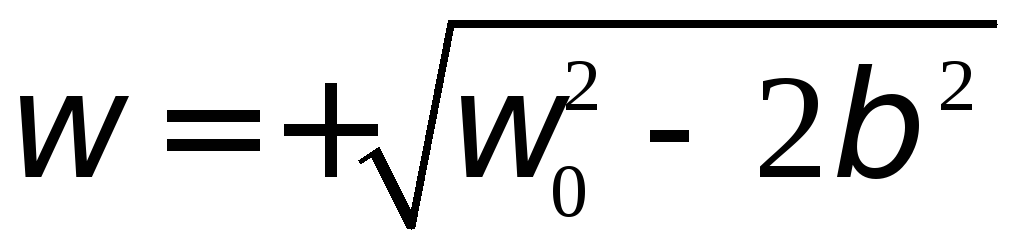
Представляет собой точку максимума амплитуды вынужденных колебаний – резонанс

Если затухание в среде мало то

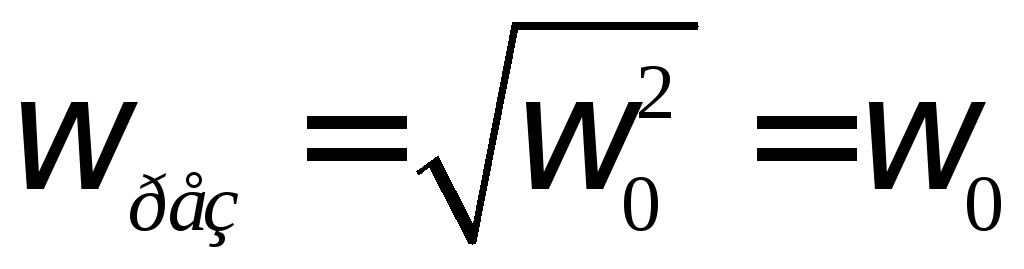
Подставив в выражение для амплитуды вынужденных колебаний

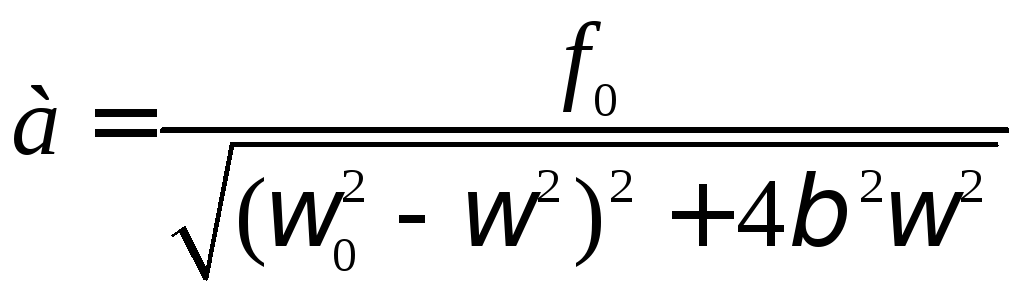
резонансную частоту

Получим выражение для амплитуды колебаний при резонансе:

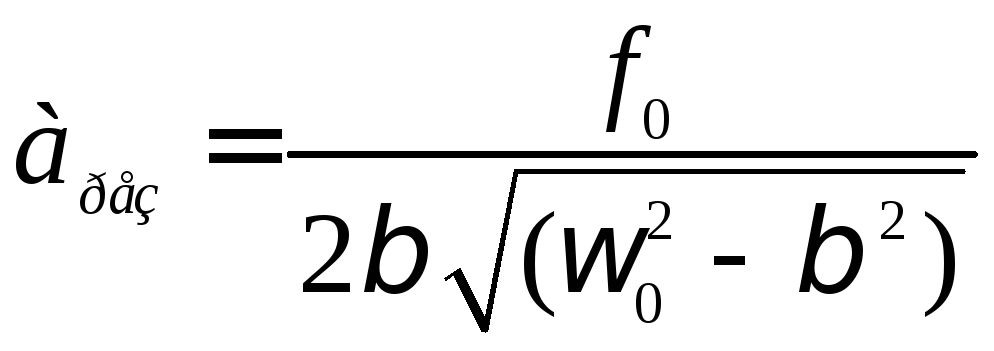
При - нет физического смысла

При наличии затухания

добротности колебательной системы