сивных элементов электрических цепей являются активное сопротивление r, индуктивность L и емкость С. Для про- стоты изложения не будем учитывать взаимную индуктив- ность. Параметры цепи почти всегда в той или иной степе- ни зависят от тока и напряжения. .Сопротивление r меня- ется при изменении тока, поскольку при этом изменяется температура проводника. Емкость конденсатора может за- висеть от напряжения, а индуктивность катушки - от то- ка. Однако во многих случаях эта зависимость настолько слабая, что ею можно пренебречь и считать параметры пассивных элементов цепи не зависящими от тока и напря- жения, В этих случаях характеристики элементов электри- ческой цепи (зависимости напряжения от тока в сопротив- лении r, заряда от напряжения на конденсаторе с емкостью С, потокосцепления от тока катушки с индуктивностью L) можно представить прямыми линиями. Такие элементы це- пи называются линейными. В линейных элементах сопро- тивление r, емкость С и индуктивность L постоянны, т. е. не зависят от тока и напряжения этих элементов.

Установившимся режимом электрической цепи при по- стоянных источниках тока и напряжения называют такое состояние, при котором ток в любой ветви и напряжение в любом узле остаются неизменными в течение сколь угод- но длительного времени [1].

Установившиеся режимы цепей, содержащих только ли- нейные пассивные элементы и постоянные по модулю и фазе источники тока, описываются линейными алгебраически- ми уравнениями- линейными уравнениям установив- шегося режима. Такие цепи называются линейными элек- трическими цепями. Этот случай соответствует расчету ус- тановившихся режимов электрических систем при задании постоянных по модулю и фазе токов нагрузки потребителей и генераторов во всех узлах электрической системы.

Если параметры пассивных элементов электрической цепи существенно зависят от тока или напряжения, т. е. ха- рактеристики этих элементов нелинейны, то и сами такие элементы называются нелинейными. В теоретической элек- тротехнике электрическая цепь, содержащая хотя бы один нелинейный элемент, называется нелинейной.

В расчетах установившихся режимов электрических си- стем нелинейность пассивных элементов, как правило, не учитывается. В этом смысле продольная часть схемы за- мещения всегда линейна. В то же время при расчетах уста- новившихся режимов электрических систем учитываются характеристики источников тока. Нелинейность источников тока соответствует заданию в узлах нагрузки потребителей или генераторов с постоянной мощностью либо заданию на- грузки ее статическими характеристиками, определяющи- ми зависимость мощности от напряжения. Установившиеся режимы электрических систем с нелинейными источниками тока описываются нелинейными алгебраическими уравне- ниями- нелинейными уравнениями установившегося ре- жима.

Статическая устойчивость - это способность электриче- ской системы восстанавливать исходный режим после ма- лого его возмущения или режим, весьма близкий к исход- ному (если возмущающее воздействие не снято). Иными словами, статическая устойчивость- это способность элек- трической системы при малом отклонении ее параметров возвращаться к режиму с исходными значениями указан- ных выше параметров. Система статически устойчива, ес- ли все действительные корни и действительные части ком- плексных корней характеристического уравнения отрица- тельны. Если нет комплексных корней с положительными действительными частями, но имеется хотя бы один поло- жительный действительный корень, то нарушение устой- чивости имеет форму апериодического ухода от исследуе- мого режима, т.е. нарушается статическая апериодическая устойчивость [7].

Уравнения узловых напряжений. Установившийся режим электрических систем и цепей рассчитывают при различ- ных способах задания исходных данных в зависимости от физической сути и цели расчета. В данном параграфе бу- дем рассматривать наиболее часто встречающийся и наи- более простой случай. Известны сопротивления и проводи- мости всех пассивных элементов электрической цепи. Кро- ме того, заданы постоянные величины всех источников тока во всех узлах, кроме балансирующего по Р и Q, и все ЭДС, а также напряжение одного узла - базисного по на- пряжению. Надо определить напряжения п узлов и токи в т ветвях¹.

В общем случае базисный по напряжению и балансиру- ющий по Р и Q узлы могут не совпадать. Как правило, при расчетах режимов электрических систем предполагают, что эти узлы совпадают. В дальнейшем для простоты изложе- ния будем считать, что базисным по напряжению и балан- сирующим по Р и Q является один и тот же (n+1)-й узел, который для краткости будем называть балансирующим.

Число независимых уравнений по первому закону Кирх- гофа равно числу независимых узлов п. Уравнение первого закона Кирхгофа для (п+1)-го узла является следствием уравнений для остальных п узлов и не входит в число не- зависимых уравнений.

Если в качестве неизвестных принять п узловых напря- жений, то установившийся режим достаточно описать только узловыми уравнениями, вытекающими из первого закона Кирхгофа и закона Ома. Уравнения узловых напря- жений следуют из первого закона Кирхгофа, если все токи в ветвях выразить через узловые напряжения и проводимо- сти ветвей. Число уравнений узловых напряжений равно числу независимых узлов п. При этом напряжение одного из узлов [(п+1)-го] может быть задано произвольно и, в частности, принято равным нулю.

Решив п уравнений узловых напряжений с п неизвест- ными, определим напряжения всех узлов. Затем вычислим токи в ветвях, которые однозначно определяются из зако- на Ома через известные напряжения узлов. Такой путь эффективнее, чем решение системы т уравнений первого и второго законов Кирхгофа для определения т независи- мых токов в ветвях, так как число ветвей в электрических системах, как правило, значительно больше числа узлов.

Уравнения узловых напряжений при напряжении ба- лансирующего узла U_б=0 для сети постоянного тока, на- пример, из четырех узлов можно записать в следующем виде:

(9.1)

где -задающий ток k-го узла, k= 1, 2, 3; -неизвест- ное узловое напряжение, т. е. напряжение между k -м узлом и балансирующим, совпадающим с базисным по U, (при kj)- взаимная проводимость узлов j и k,', - собственная проводимость узла k. Взаимная проводимость узлов j и k равна взятой с обратным знаком сумме прово- димостей ветвей, соединяющих эти узлы.

Если между двумя узлами в схеме цепи нет ветви, то со- ответствующая взаимная проводимость равна нулю. Если узлы j и k соединены одной ветвью с сопротивлением и проводимостью , то

(9.2)

Собственная проводимость k-го узла равна сумме проводимостей всех ветвей, соединенных с узлом k (в их число входят и ветви, соединяющие балансирующий узел с нулевым напряжением с узлом k). Если таких ветвей нет, то собственная проводимость узла равна сумме всех взаимных проводимостей взятой с обратным знаком. Пусть с узлом k соединено т ветвей, тогда

(9.3)

где n+1 - общее число узлов в сети, из которых п незави- симы.

Для рассматриваемой сети из четырех узлов, например,

При расчетах режимов электрических систем задающий ток равен алгебраической сумме токов источников, под- ключенных к узлу k. Токи, соответствующие генерации или потреблению, имеют разные знаки. При наличии в цепи ис- точников ЭДС в ток k-го узла входит алгебраическая сумма произведений ЭДС ветвей, соединенных с узлом k, на проводимость этих ветвей.

Будем использовать матрицу собственных и взаимных проводимостей узлов

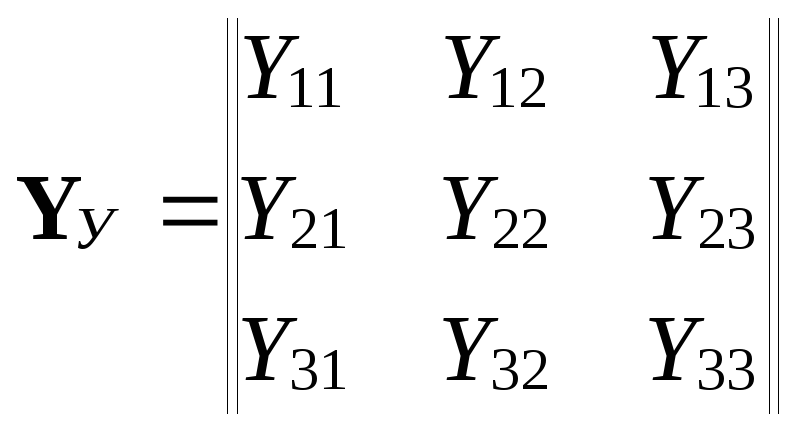(9.4)

и векторы-столбцы токов в узлах I и узловых напряжений U

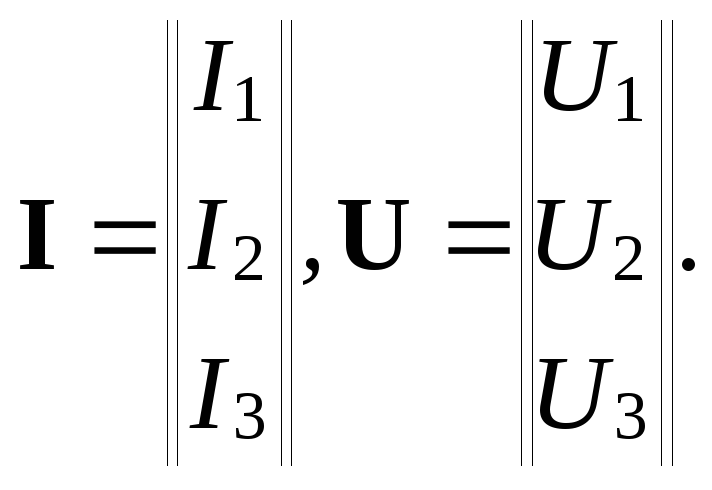(9.5)

Учитывая правило умножения матриц, систему уравне- ний узловых напряжений (9.1) можно записать в матрич- ной форме следующим образом:

(9.6)

Для цепи переменного тока узловые напряжения, токи в узлах, собственные и взаимные проводимости узлов- комплексные величины. Если аналогично (9.4) и (9.5) ис- пользовать матрицу собственных и взаимных проводимо- стей узлов с комплексными элементами , а также векторы-столбцы фазных токов в узлах и узловых между- фазных напряжений с комплексными элементами и , то систему уравнений узловых напряжений для цепи переменного тока можно записать в матричной форме:

(9.7)

В справедливости этого матричного выражения легко убедиться, если принять во внимание правило умножения матриц с комплексными элементами.

При решении на ЭВМ уравнения узловых напряжений для сети переменного тока, как правило, приводятся к си- стеме действительных уравнений порядка 2п, где п- чис- ло независимых узлов. Для этого представляют матрицы и вектор-столбцы с комплексными элементами в виде сумм матриц и вектор-столбцов с действительными элементами (при этом надо в виде такой суммы представить каждый комплексный элемент и учесть правило сложения матриц):

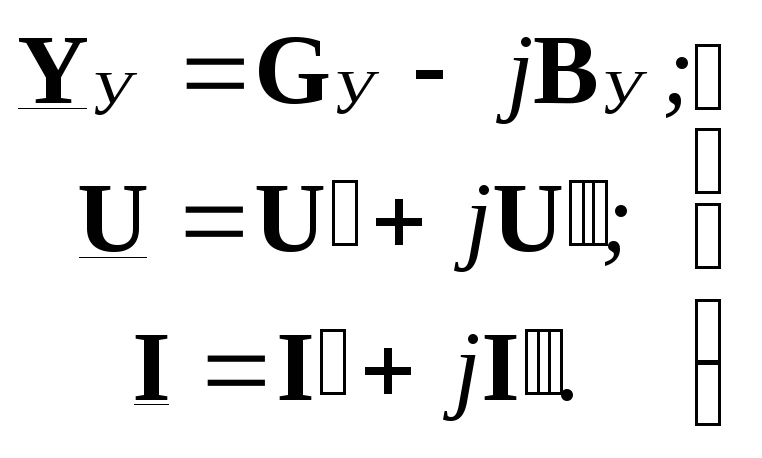(9.8)

Подставляя (9.8) в (9.7), получаем

(9.9)

Запишем отдельно действительные и мнимые матрич- ные слагаемые в последнем уравнении:

; (9.10)

(9.11)

Таким образом, систему уравнений узловых напряжений для цепи переменного тока можно записать в матричном виде следующим образом:

(9.12)

Выражение (9.12) является системой действительных уравнений порядка 2п и содержит 2п неизвестных действи- тельных и мнимых составляющих узловых напряжений .

Уравнения узловых напряжений при напряжении балан- сирующего узла для сети постоянного тока из четы- рех узлов можно записать в следующем виде:

(9.13)

Полная система уравнений узловых напряжений, анало- гичная (9.13), может быть записана в матричном виде для сети постоянного тока из (п+1)-го узла следующим обра- зом:

(9.14)

где -полная матрица узловых проводимостей порядка (п+1); -вектор-столбцы токов в узлах и напряже- ний узлов порядка (п+1).

Сумма всех токов в узлах равна нулю. Полная матрица узловых проводимостей является симметричной и вырож- денной¹, если не учитываются проводимости на землю.

Вырожденность полной матрицы следует, напри- мер, из (9.3). Полная система уравнений узловых напря- жений (9.13) или (9.14) линейно зависима. Независимыми являются лишь п уравнений узловых напряжений.

Уравнения (9.13) или (9.14) решаются обычно следую- щим образом. Один из узлов системы, например (п+1)-й, принимается за базисный по напряжению и за балансирую- щий по току. В общем случае базисным по напряжению и балансирующим по току может быть не один и тот же узел. Напряжение в этом узле предполагается изве- стным, а ток- неизвестным и равным сумме токов ос- тальныхп узлов. Токи в остальных п узлах заданы, а на- пряжения неизвестны. Вместо вырожденной системы с пол- ной матрицей (9.13) или (9.14) решается система п независимых уравнений узловых напряжений с неполной матрицей . Эту систему уравнений узловых напряжений с неполной матрицей получают из (9.13) или (9.14) отбра- сыванием последней строки и число записывают в виде, когда известные слагаемые в левой части переносят- ся вправо, т.е.

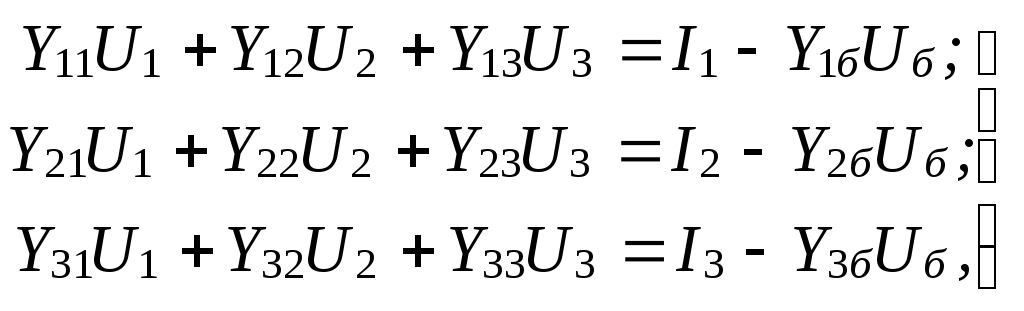(9.15)

или в матричном виде

(9.16)

где k-й элемент вектор-столбца равен, т. е.

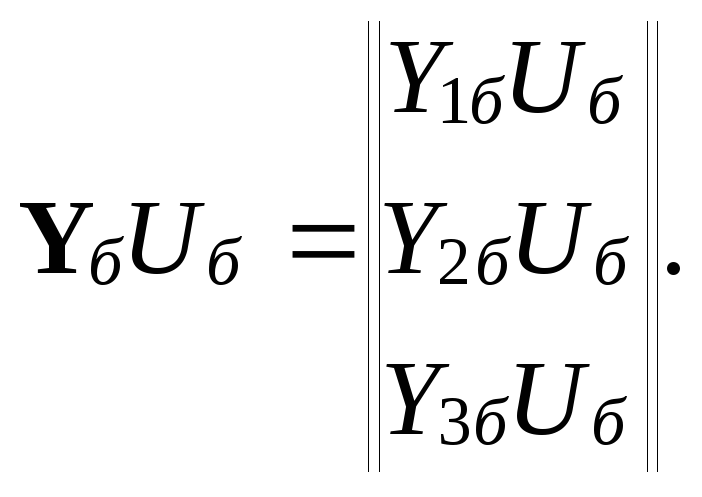(9.17)

Если в системе уравнений узловых напряжений учесть, что в соответствии с (9.3) можно представить как сум- му проводимостей, например

то (9.15) можно переписать в виде

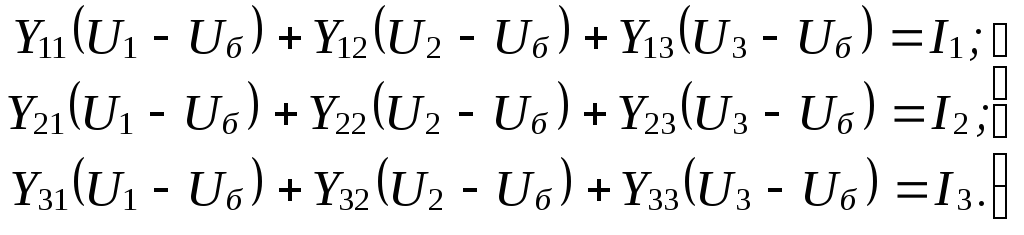
Будем использовать вектор-столбец , k-й эле- мент которого равен разности напряжений k-го и баланси- рующего узлов, т.е. для электрической системы из четырех узлов

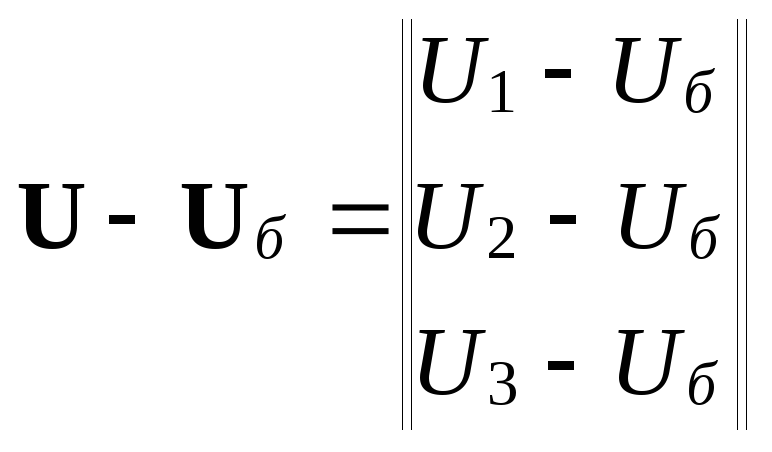. (9.18)

Тогда уравнения узловых напряжений (9.15) при в матричной форме будут иметь вид

(9.19)

Рассмотренное выше уравнение (9.6) - это частный слу- чай (9.19) при .

Изменим напряжение балансирующего узла и всех ос- тальных узлов на одно и то же значение при заданных то- ках в узлах. В этом случае не изменяются разности напря- жении между узлами. Ток в ветви, соединяющей два узла, равен разности напряжений между узлами, умноженной на проводимость ветви. Соответственно при изменении на- пряжений всех узлов на одно и то же значение в линейной цепи не изменяются токи в ветвях, потоки мощности и по- тери в ветвях, а также суммарные потери в цепях.

Можно показать, что напряжения в узлах, токи в ветвях не зависят от того, какой узел линейной электрической цепи выбирается в качестве балансирующего по току, если сум- ма токов во всех (n+1) узлах равна нулю. Поэтому выбор балансирующего узла, а также его напряжения (например, или ) не оказывают влияния на результат ра- счета установившегося режима линейных электрических систем. В этом смысле линейные уравнения узловых на- пряжений (9.6) и (9.19) эквивалентны.

Для нелинейных уравнений установившегося режима выбор балансирующего узла и значение его напряжения оказывают влияние на результат расчета режима. Поэто- му при нелинейных задающих токах в узлах уравнения (9.6) и (9.19) не эквивалентны. При расчетах нелинейных уравнений установившегося режима электрических систем используются уравнения узловых напряжений (9.19), так как обычно в качестве балансирующего узла применяется станция, ведущая по частоте (см. гл. 4), напряжение кото- рой, конечно, не равно нулю.

Для сети переменного тока система уравнений узловых напряжений может быть записана в виде комплексной си- стемы порядка п, аналогичной (9.16):

(9.20)

где - вектор-столбец,k-й элемент которого равен [см. (9.17)].

Используя выражения (9.8), можно записать (9.20) в виде системы действительных уравнений порядка 2п, аналогичной (9.12). Например, при получим

(9.21)

где и -вектор-столбцы, имеющие вид, анало- гичный (9.17); - активные и реактивные взаимные проводимости узловk-го и балансирующего.

Матрица собственных и взаимных проводимостей узлов играет важную роль в расчетах установившихся режи- мов электрических систем. Обычно в качестве исходных данных для расчетов установившихся режимов электриче- ских систем задают сопротивления продольных ветвей (ли- ний электропередачи, трансформаторов), проводимости на землю (линий электропередачи, реакторов), а также топо- логию схемы (схему соединений) электрической системы. Топология схемы, как правило, задается парами номеров узлов, соединенных ветвями. Элементы матрицы проводи- мостей рассчитываются на ЭВМ. Такой расчет очень прост и состоит практически в определении взаимных прово- димостей и в вычислении собственных проводимостей. Последние равны отрицательной сумме взаимных прово- димостей ветвей соединенных с данным узлом.

Матрица собственных и взаимных проводимостей сим- метричная, т.е. . Важнейшим свойством матрицы является большое количество нулевых элементов- ее слабая заполненность (разреженность). Как отмечалось выше, если узлы не соединены между собой ветвью, то их взаимная проводимость равна нулю. В электрической си- стеме каждый узел связан лишь с небольшим количеством соседних узлов. Пусть, например, в электрической системе из 100 узлов первый узел связан с 10 другими. Тогда в пер- вой строке и в первом столбце матрицы окажется 10 не- нулевых проводимостей, а остальные 90 равны нулю. Как правило, большинство узлов в электрических системах сое- динены со значительно меньшим количеством узлов, чем 10. В большинстве отечественных и зарубежных программ расчета установившегося режима предполагается, что пре- дельное число ветвей в 1,5 раза больше числа узлов. Это означает, что с помощью программы можно рассчитывать режимы систем, содержащих, например, не более 300 уз- лов и 450 ветвей. С учетом симметричности матрицы необ- ходимо запомнить столько ненулевых взаимных проводимо- стей, сколько ветвей в электрической системе, и столько собственных узлов проводимостей, сколько узлов в системе. Информация о схеме соединений, как правило, требует столько машинных слов памяти, сколько ветвей в системе.

Из сказанного легко убедиться, насколько меньше па- мяти требуется для запоминания ненулевых элементов мат- рицы в сравнении с тем случаем, когда пришлось бы за- помнить все элементы этой матрицы, число которых равно п². Возможность использования слабой заполненности мат- риц уравнений является важнейшим свойством, которое на- до учитывать при сопоставлении различных методов расче- тов установившихся режимов. В заключение отметим, что уравнения узловых напряжений нашли очень широкое при- менение при расчетах установившихся режимов сложных электрических систем на ЭВМ.

Матрица соединений ветвей и узлов (первая матрица инциденций)- это прямоугольная матрица, число строк которой равно числу узлов п+1. а число столбцов- числу ветвей т. Она обозначается следующим образом:

При этом номера строк i соответствуют номерам узлов, а номера столбцов j- номерам ветвей. Элементы матрицы могут принимать одно из трех значений:, ес- ли узел i является начальной вершиной ветви j; , если узел i является конечной вершиной ветви j; , если узел i не является вершиной ветви j.

Каждая строка матрицы показывает, какими вер- шинами соответствующие ветви присоединяются к данному узлу схемы; каждый столбец- какие узлы являются на- чальной и конечной вершинами данной ветви. Очевидно, что в каждом столбце матрицы может быть только од- на положительная и одна отрицательная единица; осталь- ными элементами являются нули.

Если в матрице отбросить строку, соответствующую (п+1)-му балансирующему узлу, то получим прямоуголь- ную матрицу М, в которой п строк и т столбцов.

Матрица М дает возможность записать систему неза- висимых уравнений первого закона Кирхгофа в следующем виде:

(9.22)

где столбцы токов в ветвях и задающих токов в узлах.

Матрица узловых проводимостей может быть опре- делена следующим образом [18]:

(9.23)

где - транспонированная матрица соединений ветвей и узлов ;и- диагональные матрицы сопротивле- нии и проводимостей ветвей.

9.2. Методы решения линейных уравнений узловых напряжений

Точные и итерационные методы. Методы решения линей- ных уравнений установившегося режима можно разделить на две группы: точные (или прямые) и итерационные (или приближенные).

Точными или прямыми методами называются такие, ко- торые в предположении, что все вычисления ведутся точно (без округлений), позволяют получить точные значения не- известных в результате конечного числа операций. Практи- чески все вычисления ведутся с округлениями, поэтому и значения неизвестных, полученных точным методом, бу- дут содержать погрешности. Из точных методов ниже рас- смотрим метод Гаусса и решение линейных уравнений ус- тановившегося режима с помощью обратной матрицы.

Итерационными или приближенными методами назы- вают такие, которые даже в предположении, что вычисле- ния ведутся без округлений, позволяют получить решение системы уравнений лишь с заданной точностью. Точное ре- шение системы в случае применения итерационных методов может быть получено теоретически как результат бесконеч- ного итерационного процесса. В данной главе рассмотрим два итерационных метода: простую итерацию и метод Зей- деля. Эти методы не всегда сходятся при решении линей- ных уравнений установившегося режима.

Метод последовательного исключения (метод Гаусса) - один из наиболее распространенных способов решения си- стем линейных алгебраических уравнений. Если точно вы- полнить все действия метода Гаусса, то получим точное ре- шение системы. Алгоритмы, с помощью которых может быть реализован метод Гаусса, различны. Наиболее распростра- нен алгоритм единственного деления (или алгоритм с об- ратным ходом), при обращении матриц применяется алго- ритм метода Гаусса без обратного хода (или схема Жор- дана) [18,19].

Решение по алгоритму единственного деления распада- ется на два этапа:

прямой ход- приведение системы линейных уравнений (9.1) к эквивалентной системе с треугольной матрицей

(9.24)

где коэффициенты треугольной матрицы и правые час- ти определяются по известным выражениям, соответст- вующим исключению неизвестных [19];

обратный ход- вычисление неизвестных в соответствии с (9.24).

Общее количество арифметических действий в методе Гаусса несколько меньше п³, где п- число неизвестных. Машинное время, необходимое для выполнения арифмети- ческих операций метода Гаусса, пропорционально кубу чис- ла неизвестных.

При расчете режима сети переменного тока по методу Гаусса на ЭВМ система комплексных уравнений, как пра- вило, заменяется эквивалентной системой с действительны- ми переменными порядка 2п, где (п+1)- число узлов схемы.

Достоинство метода Гаусса состоит в том, что его при- менение гарантирует получение решения в результате вы- полнения определенного числа арифметических операций, причем число необходимых операций определяется только порядком системы п. В этом состоит преимущество метода Гаусса и других точных методов перед приближенными, или итерационными, для которых число необходимых ариф- метических вычислений зависит не только от порядка си- стемы, но и от заранее неизвестного количества шагов, за которое сойдется итерационный процесс.

Недостаток метода Гаусса состоит в необходимости за- поминать матрицу элементов системы уравнений. Для рас- чета сложных электрических систем эффективное примене- ние метода Гаусса невозможно без использования специ- альных методов, учитывающих слабую заполненность матрицы узловых проводимостей. К сожалению, такой учет алгоритмически достаточно сложен и, кроме того, его при- менение не полностью устраняет недостатки метода Гаус- са, связанные с необходимостью использования большой памяти ЭВМ при расчетах режимов сложных электричес- ких систем. Подробнее этот вопрос рассмотрен в гл. 10.

Решение с помощью матрицы . Матрицей собственных и взаимных сопротивлений узлов , обратной по отноше- нию к матрице собственных и взаимных проводимостей уз- лов, называют такую матрицу

(9.25)

при которой выполняется условие

(9.26)

где Е - единичная матрица.

Например,

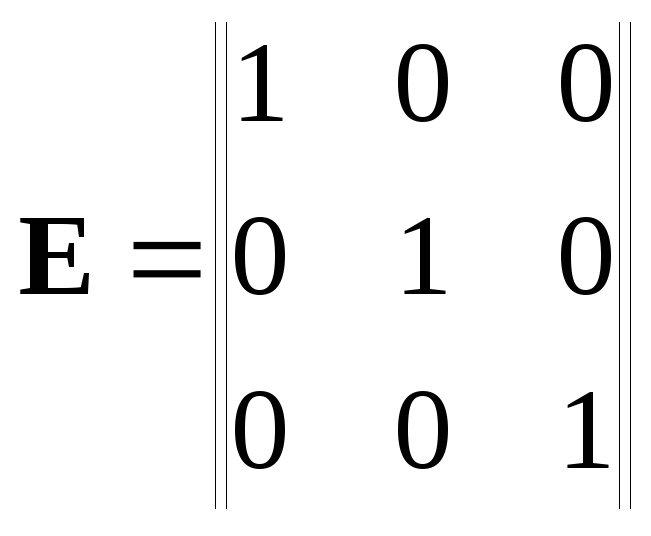(9.27)

- единичная матрица третьего порядка.

Умножим обе части матричного уравнения узловых на- пряжений (9.6) с помощью обратной матрицы и получим

(9.28)

или с учетом (9.26)

(9.29)

Формула (9.29) дает решение уравнения узловых на- пряжений (9.6) с помощью обратной матрицы .

Решение уравнений узловых напряжений с помощью об- ратной матрицы при напряжении балансирующего узла определяется следующим выражением, вытекающим из (9.19):

(9.30)

или

(9.31)

где и I- вектор-столбцы узловых напряжений и токов в узлах (9.5); - вектор-столбец, каждый элемент кото- рого равен напряжению балансирующего узла:

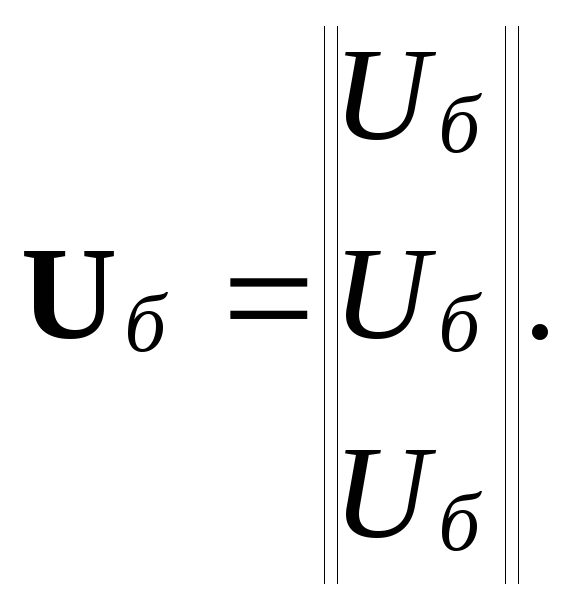
При расчете режимов электрических систем переменного тока напряжения узлов определяются по выражению, ана- логичному (9.31), в котором все матрицы и вектор-столбцы состоят из комплексных элементов:

(9.32)

Обычно напряжение балансирующего узла принимается равным действительной величине. Поскольку это не обяза- тельно, для общности в (9.32) вектор-столбец , каждый элемент которого равен напряжению балансирующего уз- ла, записан как комплексный.

В матрице собственных и взаимных сопротивлений уз- лов нет нулевых элементов, т.е. эта матрица заполнен- ная. Отсутствие нулевых элементов в матрице существенно понижает эффективность ее использования при расчетах ус- тановившихся режимов электрических систем.

Применение обратной матрицы для решения действи- тельной системы порядка п>4 редко употребляется на практике. Применение формул Крамера для решения ли- нейной системы нецелесообразно уже при п>3. Соответст- венно применение матрицы для выполняемого лишь 1 раз расчета установившегося режима менее эффективно, чем исключение Гаусса, даже без учета слабой заполнен- ности матрицы узловых проводимостей.

Практика расчетов режимов электрических систем при- водит к необходимости многократного расчета режимов для одной и той же электрической системы при изменении то- ков в узлах либо при незначительных изменениях схемы соединений и параметров электрической сети. В таких мно- гократных расчетах режимов применение матрицы име- ет важное преимущество, которое состоит в возможности быстрой корректировки матрицы при небольших измене- ниях схемы соединений или параметров сети. Разработаны эффективные методы такой корректировки. Применение матрицы эффективно также при расчетах режимов элек- трических систем с тяговой нагрузкой и при расчетах то- ков коротких замыканий.

Простая итерация н метод Зейделя - простейшие из ите- рационных методов. Рассмотрение простой итерации важно для понимания сути применения итерационных методов расчета установившихся режимов электрических систем. Для определенности вначале ограничимся рас- смотренной выше системой уравнений третьего поряд- ка (9.1).

Предполагая, что диагональные элементы , разрешим первое уравнение системы (9.1) от- носительно , второе- относительно , а третье- относительно . Тогда получим систему, эквивалент- ную (9.1):

(9.33)

где

(9.34)

Зададим начальные приближения неизвестных , , . Подставляя их в правые части системы (9.33), получаем первые приближения , , . Вычисление первого приближения неизвестных соответствует первому шагу итерационного процесса. Полученные первые прибли- жения могут быть таким же образом использованы для по- лучения вторых, третьих и последующих приближений. Ис- пользуя значения переменных, полученных на предыдущем, i-м шаге, можно получить (i+1)-е приближения неизвест- ных:

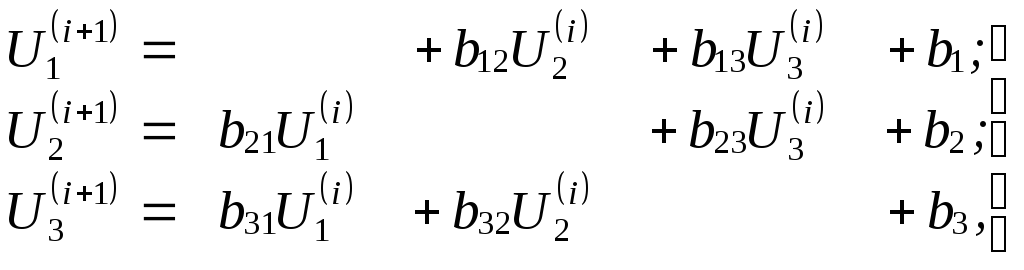(9.35)

Введем матрицу и вектор-столбцы:

Диагональные элементы матрицы В равны нулю, т. е. , а недиагональные элементы (т.е. при) со- впадают с коэффициентами систем (9.33) или (9.35). Учи- тывая правило умножения и сложения матриц, систему (9.33) можно записать в матричной форме:

. (9.36)

Аналогично итерационное выражение (9.35) можно записать в матричном виде:

. (9.37)

Элементы матрицы В- безразмерные величины, а элемен- ты вектора b имеют размерность напряжений.

Итерационный процесс, определяемый выражением (9.35) или (9.37), называется простой итерацией.

Для сети переменного тока комплексные уравнения уз- ловых напряжений представляются в виде системы дейст- вительных уравнений. Затем к полученной системе действи- тельных уравнений применяется метод простой итерации. В принципе возможно применение простой итерации по вы- ражению (9.35) или (9.37) к комплексным числам. При практических расчетах на ЭВМ такой путь, как правило, не используется.

Метод Зейделя представляет собой незначительную мо- дификацию простой итерации. Основная его идея в отли- чие от простой итерации заключается в том, что найденное (i+1)-е приближение (k-1)-го напряжения сразу же используется для вычисления следующего, k-го напря- жения . Иными словами, полученное (i+1)-е значение напряжения сразу же используется для вычисления (i+1)- го значения напряжений и т.д. Таким образом, для системы (9.1) итерационный процесс метода Зейделя опи- сывается следующим выражением:

(9.38)

По методу простой итерации (i+1)-е приближение k-го напряжения для системы п-го порядка вычисляется по следующему выражению:

(9.39)

По методу Зейделя (i+1)-е приближение k-го напря- жения вычисляется так:

(9.40)

Можно показать, что метод Зейделя эквивалентен про- стой итерации (9.37), но с другой матрицей и другим век- тором.

Как правило, метод Зейделя надежнее и быстрее схо- дится, чем метод простой итерации. Кроме того, метод Зей- деля требует несколько меньшей памяти, чем простая ите- рация, так как необходимо помнить только один вектор переменных. Действительно, при решении по Зейделю, напри- мер, уравнений узловых напряжений сразу после вычисле- ния (i+1)-е приближение k-го узлового напряжения записывается в ту же ячейку памяти, где ранее хранилось i-е приближение . При использовании простой итерации необходимо помнить два вектора узловых напряжений, со- ответствующих i-му и (i+1)-му шагам.

Алгоритмическая реализация метода Зейделя столь же проста, как и простой итерации. Единственное изменение в алгоритме расчета состоит в засылке вычисленного в то же место памяти, где ранее хранилось .

Поскольку метод простой итерации не имеет никаких преимуществ перед методом Зейделя, при практических ра- счетах установившихся режимов электрических систем на ЭВМ всегда используется метод Зейделя, а не простая ите- рация.

Если метод Зейделя сходится быстро и для решения си- стемы п-го порядка требуется менее п шагов, то при расче- те на ЭВМ получим выигрыш во времени в сравнении с точ- ными методами, например с методом Гаусса. Это вытекает из того, что число арифметических операций, необходимых для одного шага метода Зейделя, пропорционально п² а об- щее число арифметических операций, например в методе Гаусса, пропорционально п³. Приведенное соотношение чис- ла операций справедливо для расчетов установившегося режима, если не учитывается слабая заполненность матриц узловых проводимостей. В то же время и в случае учета слабой заполненности этих матриц метод Зейделя, если он сходится быстро, требует меньше времени ЭВМ, чем точ- ные методы.

Важное достоинство метода Зейделя состоит в простоте алгоритма и в удобстве его реализации на ЭВМ. Он осо- бенно эффективен при учете слабой заполненности матрицы узловых проводимостей, поскольку алгоритм такого учета в методике Зейделя весьма прост. В результате экономия памяти при использовании метода Зейделя становится тем существенней, чем больше узлов содержит электрическая система. Применение специальных методов учета слабой заполненности при применении точных методов несколько уменьшает преимущество метода Зейделя с точки зрения необходимого объема памяти ЭВМ. Однако в точных мето- дах такой учет алгоритмически сложен и даже при его при- менении метод Зейделя все равно требует меньше памяти ЭВМ. Вопросы экономии памяти играют важную роль при сопоставлении различных методов расчета режимов и бо- лее подробно рассмотрены в гл. 10.

Существенный недостаток метода Зейделя- его мед- ленная сходимость или даже расходимость при расчете электрических систем с устройствами продольной компен- сации, с трехобмоточными трансформаторами, когда сопро- тивление обмотки среднего напряжения очень мало, а так- же при расчетах предельных и неустойчивых режимов.