
- •Федеральное агентство по образованию
- •Т. А. Ширабакина основы автоматики и системы автоматического управления
- •Предисловие
- •Введение
- •1. Методические рекомендации по выполнению лабораторных работ по исследованию линейных систем автоматического управления
- •1.1. Исследование частотных характеристик системы автоматического управления
- •Контрольные вопросы
- •1.2. Преобразование структурных схем сау. Передаточная функция системы
- •Контрольные вопросы
- •1.3. Исследование устойчивости сау по критерию Рауса
- •Контрольные вопросы
- •1.4. Исследование устойчивости сау по критерию Гурвица
- •Контрольные вопросы
- •1.5. Исследование устойчивости сау частотным критерием Михайлова
- •Контрольные вопросы
- •2. Методические рекомендации по курсовомупроектированию
- •2.1. Задание на проект
- •2.2. Пояснения к выполнению проекта
- •2.2.1. Элементы расчетной структурной схемы. Передаточные функции
- •2.2.2. Структурные схемы эмс, их возможности и характеристики
- •2.2.3. Статические характеристики
- •Механические характеристики при отрицательных обратных связях
- •Статические характеристики при управлении перемещением
- •2.2.4. Синтез автоматизированных систем
- •2.2.5. Основные приемы оптимального синтеза структур сау
- •2.2.6. Примеры синтеза
- •3. Задания для самостоятельной работы
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Заключение
- •Библиографический список
- •Основы автоматики и системы автоматического управления
1. Методические рекомендации по выполнению лабораторных работ по исследованию линейных систем автоматического управления
Для изучения общих принципов построения элементов автоматики и методик анализа линейных автоматических систем, формирования практических навыков синтеза автоматических систем целесообразно выполнить ряд лабораторных работ.
1.1. Исследование частотных характеристик системы автоматического управления
Для анализа и синтеза систем автоматического регулирования и управления широкое использование получили частотные характеристики.
Выражения
для частотных характеристик систем
могут быть легко получены из передаточных
функций путём замены
![]() на
на
![]() .
.
Физически частотная характеристика системы имеет место при подаче на вход системы гармонического воздействия при изменении частоты от нуля до бесконечности и сохранении постоянной амплитуды входного сигнала на всём диапазоне изменения частот [1, 3].
К частотным характеристикам системы относятся:
W (j) – амплитудно-фазовая частотная характеристика (АФЧХ);
U () – вещественная частотная характеристика;
V () – мнимая частотная характеристика;
A () – амплитудная частотная характеристика (АЧХ);
![]() ()
– фазовая частотная характеристика
(ФЧХ);
()
– фазовая частотная характеристика
(ФЧХ);
L
()
– логарифмическая амплитудная частотная
характеристика (ЛАЧХ);![]()
![]() ()
– логарифмическая фазовая частотная
характеристика (ЛФЧХ).
()
– логарифмическая фазовая частотная
характеристика (ЛФЧХ).
Соотношения между этими характеристиками определяются следующими выражениями:
![]() ;
;
![]() ;
;
![]()
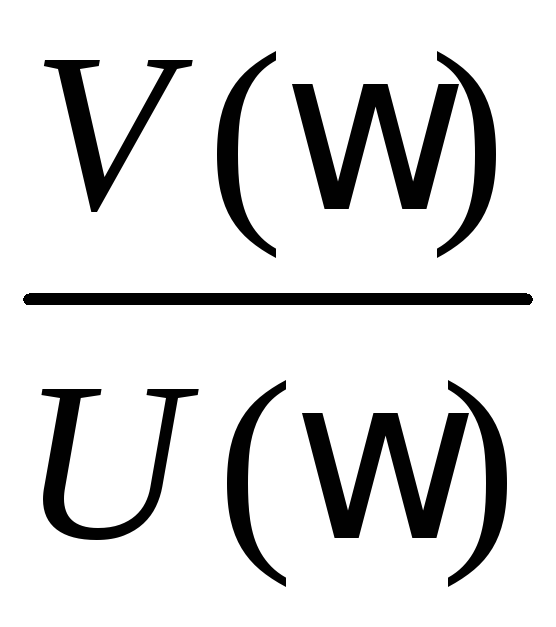 ;
;
![]()
![]()
![]() .
.
Ценность частотных характеристик заключается в том, что они косвенно, без решения дифференциального уравнения системы, позволяют судить о поведении системы и определить ряд показателей качества регулирования, рассчитать корректирующие звенья системы для получения заданных динамических показателей.
Наибольшее применение получили характеристики разомкнутой системы благодаря их наглядности и простоте построения. Особенно это касается логарифмических частотных характеристик, позволяющих выполнить синтез системы наиболее простым образом.
Рассмотрим построение логарифмических характеристик разомкнутой системы, если передаточная функция
![]() (1.1)
(1.1)
где
k
– коэффициент передачи;
![]() – постоянные времени звеньев, входящих
в систему.
– постоянные времени звеньев, входящих
в систему.
Если
![]() ,
то сопрягающие частоты
,
то сопрягающие частоты
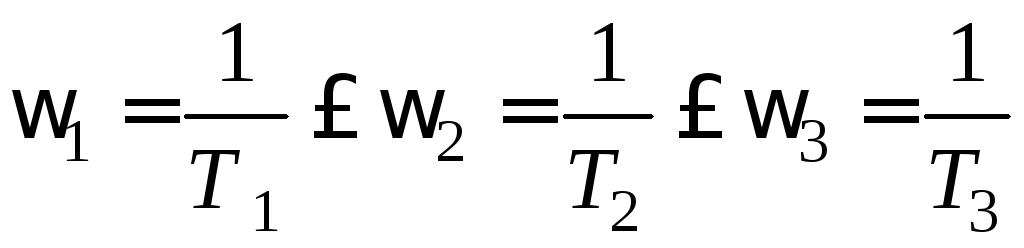 .
.
Амплитудно-фазовая частотная характеристика системы
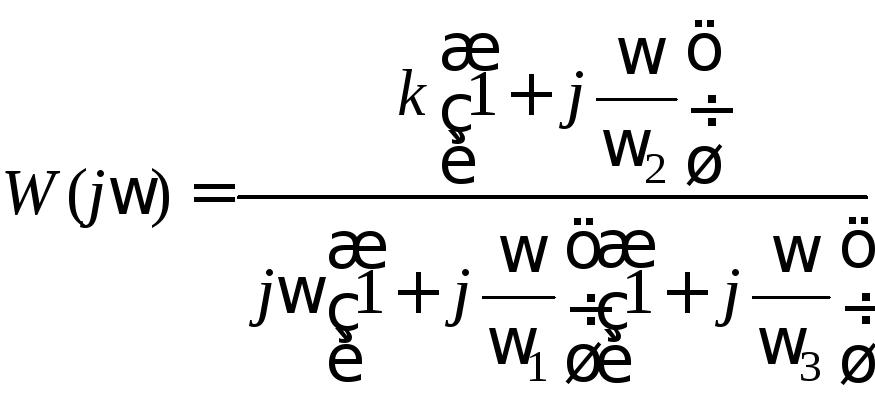 .
(1.2)
.
(1.2)
Выполнив преобразования, получим:
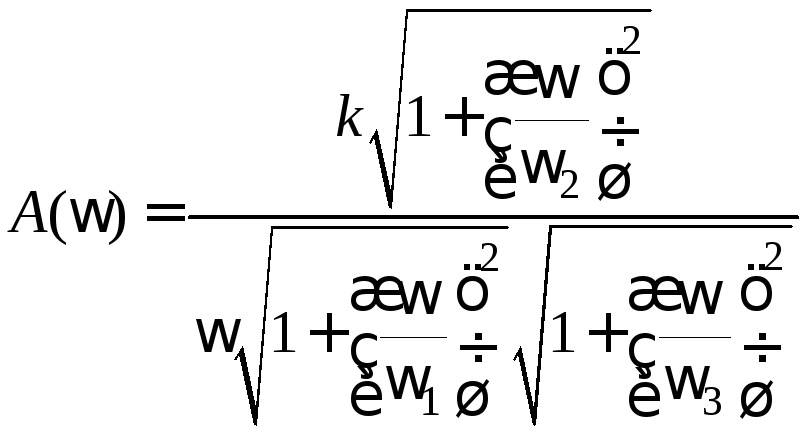 ;
(1.3)
;
(1.3)
 .
(1.4)
.
(1.4)
Прологарифмируем выражение (1.3):
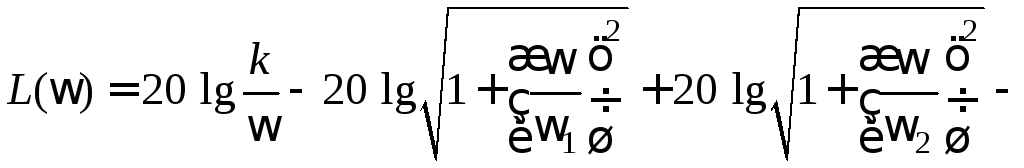
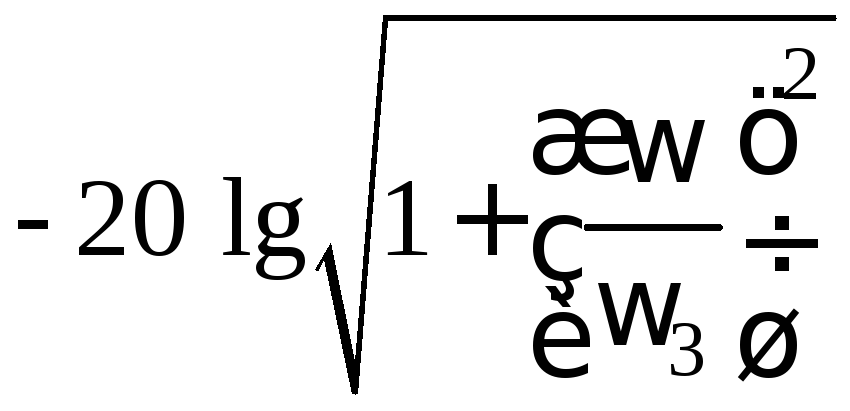 .
(1.5)
.
(1.5)
При
построении ЛАЧХ нужно учесть, что в
выражении
 для
значений
для
значений
![]() пренебрегают вторым слагаемым по
сравнению с 1. Для значений
пренебрегают вторым слагаемым по
сравнению с 1. Для значений
![]() пренебрегают 1. Ошибка не превышает
нескольких децибелов.
пренебрегают 1. Ошибка не превышает
нескольких децибелов.
Если в выражении (1.2) m сопрягающих частот, то ЛАЧХ состоит из (m+1) асимптот.
В
выражении (1.2) три частоты, значит
характеристика содержит 4 асимптоты.
Каждую асимптоту
![]() строят в диапазоне
строят в диапазоне
![]() .
Первая асимптота для
.
Первая асимптота для
![]() ;
последняя для
;
последняя для
![]() .
Построим логарифмическую амплитудную
частотную характеристику (рис. 1.1).
.
Построим логарифмическую амплитудную
частотную характеристику (рис. 1.1).
Асимптота соответствует
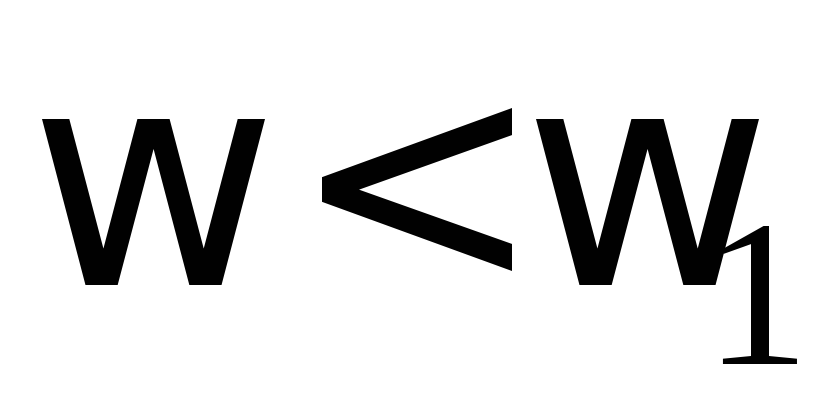 :
:
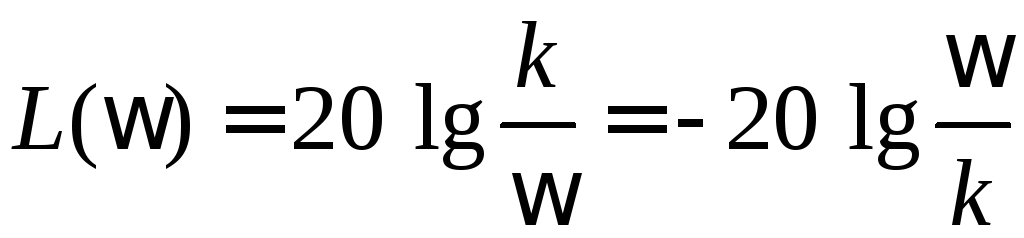 .
.
Это
уравнение прямой, проходящей через
точку
![]() с наклоном –20 дБ/дек. Заканчивается
в точке
с наклоном –20 дБ/дек. Заканчивается
в точке![]() .
.
Асимптота соответствует изменению частоты
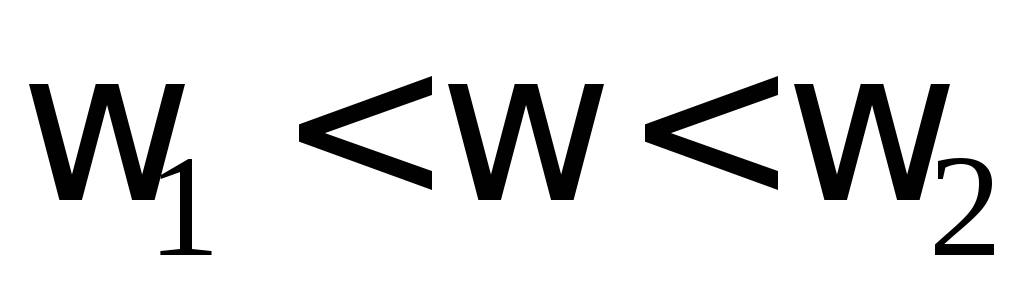 .
.
Из выражения (1.5) получаем:
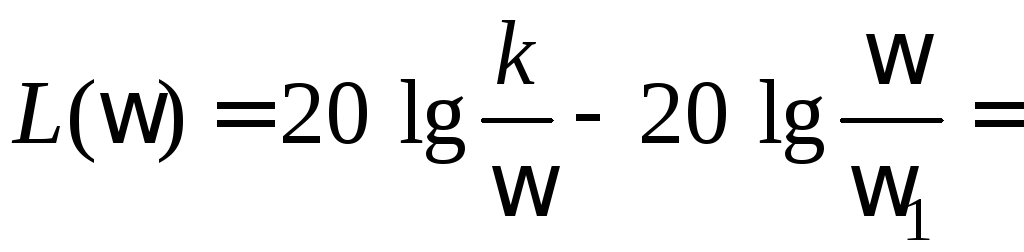
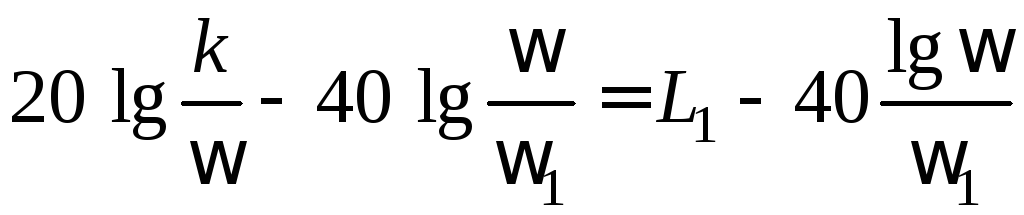 .
.
Третья асимптота строится при
 :
:
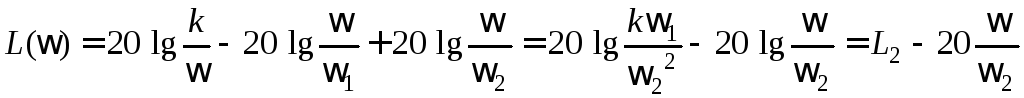 .
.
Четвертая асимптота строится при частоте больше
 :
:
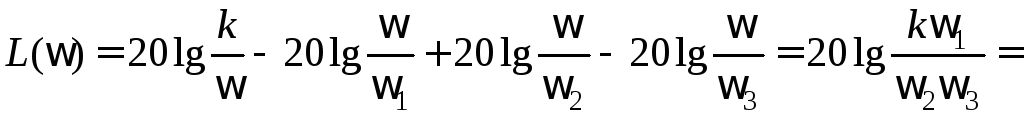
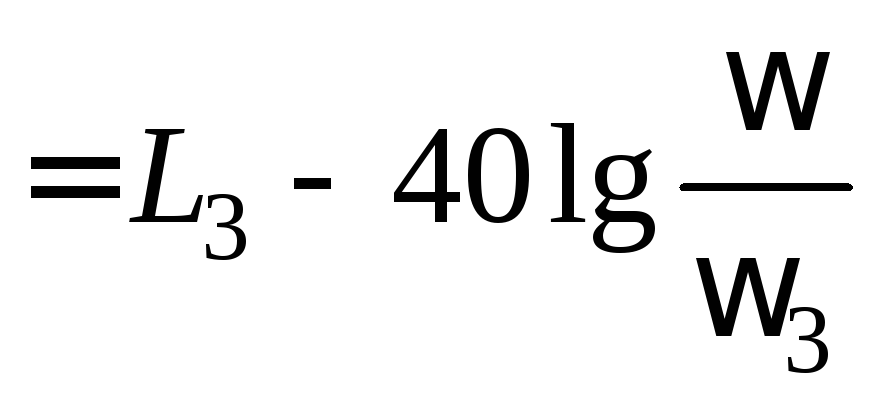 .
.

Рис. 1.1. Логарифмическая амплитудная частотная характеристика
Итак, при построении логарифмической характеристики необходимо выполнять следующее правило: наклон асимптоты изменяется:
на –20 дБ/дек, если k принадлежит множителю
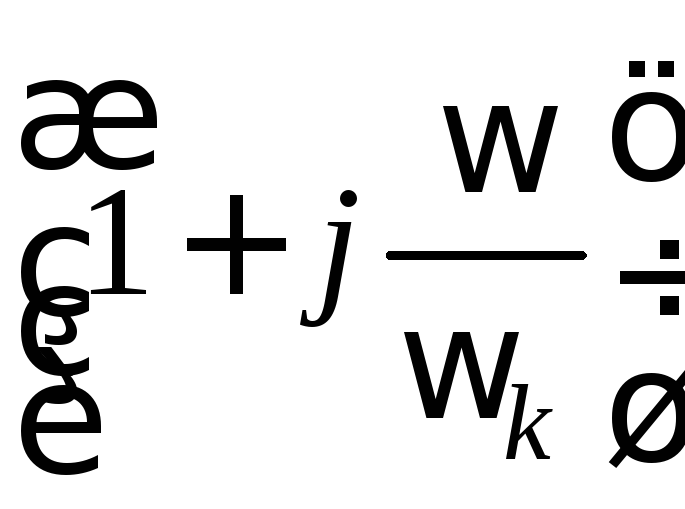 ,
стоящему в знаменателе передаточной
функции;
,
стоящему в знаменателе передаточной
функции;на +20 дБ/дек, если k принадлежит множителю
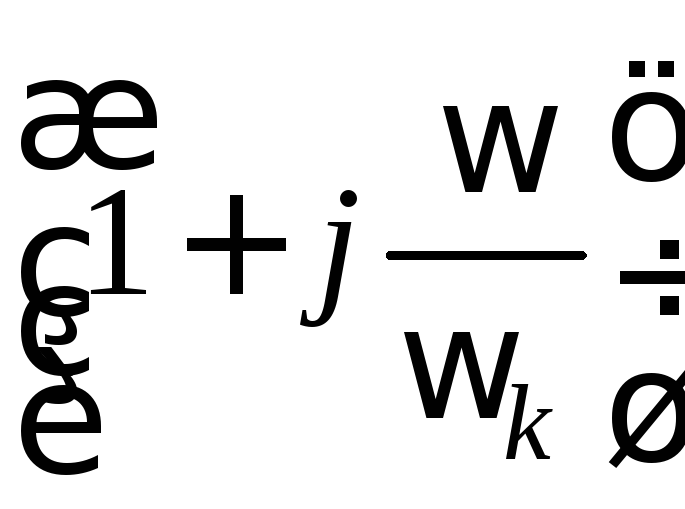 ,
стоящему в числителе передаточной
функции.
,
стоящему в числителе передаточной
функции.
Логарифмическая фазовая частотная характеристика представляет собой фазовую частотную характеристику, построенную в логарифмическом масштабе частот.
Задание. Построить частотные характеристики следящей системы с асинхронным двухфазовым двигателем в разомкнутом состоянии (рис. 1.2).
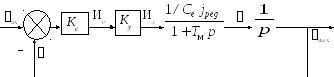
Рис. 1.2. Структурная
схема системы:
![]() – преобразующий коэффициент преобразующего
устройства;
– преобразующий коэффициент преобразующего
устройства;![]() – коэффициент усиления усилителя;
– коэффициент усиления усилителя;![]() – скоростной коэффициент двигателя;
– скоростной коэффициент двигателя;![]() – электромеханическая
постоянная
двигателя;
– электромеханическая
постоянная
двигателя;![]() – передаточное число редуктора
– передаточное число редуктора
Численные значения параметров приведены в таблице 1.1.
Таблица 1.1
Параметры системы
|
Вариант |
Кс, В/град |
Ку |
Се, В/град |
Тм, с |
jpeg |
|
1 |
1 |
64 |
0,311 |
0,075 |
8 |
|
2 |
2 |
60 |
0,3 |
0,07 |
7 |
|
3 |
1 |
50 |
0,2 |
0,06 |
10 |
|
4 |
2 |
30 |
0,25 |
0,065 |
7 |
Окончание табл. 1.1
|
Вариант |
Кс, В/град |
Ку |
Се, В/град |
Тм, с |
jpeg |
|
5 |
1 |
40 |
0,28 |
0,055 |
8 |
|
6 |
2 |
50 |
0,29 |
0,05 |
9 |
|
7 |
1 |
60 |
0,31 |
0,05 |
10 |
|
8 |
2 |
35 |
0,30 |
0,045 |
9 |
|
9 |
1 |
45 |
0,29 |
0,07 |
8 |
|
10 |
2 |
55 |
0,28 |
0,075 |
7 |
|
11 |
3 |
50 |
0,25 |
0,068 |
9 |
|
12 |
3 |
40 |
0,32 |
0,065 |
10 |
|
13 |
2 |
70 |
0,27 |
0,05 |
11 |
|
14 |
1,5 |
28 |
0,25 |
0,072 |
6 |
|
15 |
1,8 |
32 |
0,32 |
0,074 |
11 |
|
16 |
2,5 |
43 |
0,35 |
0,08 |
5 |
|
17 |
2,6 |
45 |
0,38 |
0,06 |
6 |
|
18 |
2,5 |
40 |
0,30 |
0,05 |
5 |
|
19 |
1,5 |
40 |
0,26 |
0,06 |
10 |
|
20 |
1 |
62 |
0,25 |
0,065 |
7 |
|
21 |
1,5 |
64 |
0,28 |
0,068 |
8 |
|
22 |
1,8 |
65 |
0,29 |
0,07 |
9 |
|
23 |
2,1 |
68 |
0,30 |
0,075 |
10 |
|
24 |
2,5 |
70 |
0,35 |
0,071 |
11 |
|
25 |
2,8 |
75 |
0,40 |
0,068 |
12 |
|
26 |
2,3 |
60 |
0,31 |
0,065 |
13 |
|
27 |
3 |
70 |
0,25 |
0,05 |
10 |
|
28 |
2 |
75 |
0,26 |
0,06 |
15 |
|
29 |
3 |
63 |
0,27 |
0,07 |
10 |
|
30 |
3,5 |
60 |
0,2 |
0,07 |
12 |
|
31 |
3,2 |
50 |
0,25 |
005, |
10 |
|
32 |
1,9 |
55 |
0,1 |
0,06 |
8 |
|
33 |
3 |
20 |
0,2 |
0,05 |
10 |
|
34 |
2,2 |
15 |
0,03 |
0,04 |
10 |
|
35 |
2,4 |
20 |
0,02 |
0,05 |
10 |
