
Делимость и алгоритм Евклида
Понятие делимости является одним из фундаментальных понятий теории чисел.
Определение 1.
Для данных
целых чисел
![]() и
и
![]() говорят, что
говорят, что
![]() делит
делит
![]() (или иными словами, что
(или иными словами, что
![]() делится на
делится на
![]() ),
и обозначают
),
и обозначают
![]() если
существует такое целое число
если
существует такое целое число
![]() ,
что
,
что
![]() :
:
|
|
|
(1) |
В этом случае
число
![]() называют делителем числа
называют делителем числа
![]() .
Очевидно, что любое целое число
.
Очевидно, что любое целое число
![]() имеет, по крайней мере, два положительных
делителя: 1 и
имеет, по крайней мере, два положительных
делителя: 1 и
![]() .
.
Определение 2.
Собственным
делителем числа
![]() называют любой положительный делитель,
не равный
называют любой положительный делитель,
не равный
![]() .
.
Определение 3.
Нетривиальным
делителем числа
![]() называют любой положительный делитель,
не равный 1 или
называют любой положительный делитель,
не равный 1 или
![]() .
.
Введенное понятие нетривиального делителя используем для определения понятия простого числа.
Определение 4. Простым (prime) называют целое число большее 1, не имеющее нетривиальных делителей.
Определение 5. Составным (complex) называют число, имеющее, по крайней мере, один нетривиальный делитель.
Непосредственно из определения делимости (1) следуют свойства данного отношения:
1. Если
![]() делит
делит
![]() ,
и
,
и
![]() − любое целое число, то
− любое целое число, то
![]() делит произведение
делит произведение
![]() :
:
|
|
|
|
2. Если
![]() делит
делит
![]() ,
а
,
а
![]() ,
в свою очередь, делит
,
в свою очередь, делит
![]() ,
то
,
то
![]() делит
делит
![]() :
:
|
|
|
|
3. Если
![]() делит
делит
![]() ,
и
,
и
![]() делит
делит
![]() ,
то
,
то
![]() делит
делит
![]() :
:
|
|
|
|
В дальнейшем, для
некоторого простого
![]() и целого, неотрицательного числа
и целого, неотрицательного числа
![]() запись вида
запись вида
![]() будем использовать для обозначения
того факта, что
будем использовать для обозначения
того факта, что
![]() − наивысшая степень
− наивысшая степень
![]() ,
делящая
,
делящая
![]() :
:
|
|
|
|
В этом случае
говорят, что
![]() точно делит
точно делит
![]() .
.
Основная теорема
арифметики утверждает, что любое
натуральное число
![]() может быть представлено в виде произведения
простых делителей единственным образом,
с точностью до перестановки. Данное
представление принято записывать в
форме произведения делителей в
соответствующих степенях, располагая
простые числа в порядке возрастания.
может быть представлено в виде произведения
простых делителей единственным образом,
с точностью до перестановки. Данное
представление принято записывать в
форме произведения делителей в
соответствующих степенях, располагая
простые числа в порядке возрастания.
Пример 1. Рассмотрим
разложение числа
![]() в виде произведения простых сомножителей:
в виде произведения простых сомножителей:
![]() .
.
Из основной теоремы арифметики следуют нижеприведенные свойства делимости:
4. Простое число
![]() делит произведение целых чисел
делит произведение целых чисел
![]() ,
в том и только в том случае, когда
,
в том и только в том случае, когда
![]() делит
делит
![]() ,
либо
,
либо
![]() делит
делит
![]() :
:
|
|
|
|
5. Если
![]() делит
делит
![]() и,
и,
![]() делит
делит
![]() ,
и если
,
и если
![]() и
и
![]() не имеют общих делителей больших 1, то
произведение
не имеют общих делителей больших 1, то
произведение
![]() делит
делит
![]() :
:
|
|
|
|
Из основной теоремы
арифметики следует также простой способ
отыскания всех делителей
![]() по его разложению. А именно, любой
делитель
по его разложению. А именно, любой
делитель
![]() числа
числа
![]() должен быть произведением тех же простых
сомножителей в степенях, не превышающих
степени, точно делящие
должен быть произведением тех же простых
сомножителей в степенях, не превышающих
степени, точно делящие
![]() .
.
Таким образом,
если
![]() ,
то
,
то
![]() для некоторого
для некоторого
![]() ,
удовлетворяющего условию
,
удовлетворяющего условию
![]() .
.
Пример 2. Для
нахождения делителей числа
![]() необходимо взять
необходимо взять
![]() в степени
в степени
![]() или
или
![]() ,
умножить на
,
умножить на
![]() в степени
в степени
![]() или
или
![]() ,
на
,
на
![]() в степени
в степени
![]() или
или
![]() и на
и на
![]() в степени
в степени
![]() или
или
![]() .
.
В этих условиях
число всех сомножителей есть произведение
числа способов выбора степени для
каждого простого сомножителя, которое,
в свою очередь, равно
![]() .
Иначе говоря, число
.
Иначе говоря, число
![]() имеет
имеет
 различных делителей.
различных делителей.
Пример 3. Число
![]() имеет
имеет
![]() различных делителей.
различных делителей.
Определение
7. Наибольшим
общим делителем двух данных чисел
![]() и
и
![]() (обозначается
(обозначается
![]() ),
не равных одновременно нулю, называется
наибольшее целое число
),
не равных одновременно нулю, называется
наибольшее целое число
![]() ,
делящее одновременно
,
делящее одновременно
![]() и
и
![]() .
.
Нетрудно показать, что приведенное выше определение эквивалентно следующему.
Определение 8.
![]() − есть единственное целое положительное
число, которое делит
− есть единственное целое положительное
число, которое делит
![]() и
и
![]() ,
и делится при этом на любой их общий
делитель.
,
и делится при этом на любой их общий
делитель.
Из школьного курса
математики известен следующий способ
нахождения наибольшего общего делителя
двух положительных чисел по известному
разложению на множители. Для отыскания
![]() необходимо взять все простые числа,
входящие в оба разложения, и каждое
возвести в степень, равную минимуму из
двух соответствующих показателей.
необходимо взять все простые числа,
входящие в оба разложения, и каждое
возвести в степень, равную минимуму из
двух соответствующих показателей.
Пример 4. Пусть
дано
![]() и
и
![]() .
Тогда
.
Тогда
![]() .
.
Определение 9.
Наименьшим
общим кратным двух данных чисел
![]() и
и
![]() (обозначается
(обозначается
![]() ),
не равных одновременно нулю, называется
наименьшее целое положительное число
),
не равных одновременно нулю, называется
наименьшее целое положительное число
![]() ,
делящееся одновременно на
,
делящееся одновременно на
![]() и
и
![]() .
.
Имея разложение
на простые множители чисел
![]() и
и
![]() ,
можно получить значение
,
можно получить значение
![]() ,
взяв все простые, входящие хотя бы в
одно из разложений, и каждое возвести
в степень, равную максимальной из
имеющихся в двух разложениях.
,
взяв все простые, входящие хотя бы в
одно из разложений, и каждое возвести
в степень, равную максимальной из
имеющихся в двух разложениях.
Кроме того, нетрудно показать, что наибольший общий делитель и наименьшее общее кратное связаны следующим соотношением:
|
|
|
|
Рассмотренный
метод отыскания
![]() двух чисел основывается на использовании
представления этих чисел в виде
произведения простых множителей. Однако
на практике такой метод мало применим,
так как разложение числа, как правило,
неизвестно, и его отыскание (как будет
показано в дальнейшем) является сложной
математической задачей.
двух чисел основывается на использовании
представления этих чисел в виде
произведения простых множителей. Однако
на практике такой метод мало применим,
так как разложение числа, как правило,
неизвестно, и его отыскание (как будет
показано в дальнейшем) является сложной
математической задачей.
Другим, наиболее известным способом отыскания наибольшего общего делителя двух чисел является алгоритм, впервые изложенный в трудах древнегреческого математика Евклида (IV-III вв. до н.э.), и потому называемый по его имени.
В общем случае алгоритм Евклида заключается в следующем.
Пусть
![]() ,
,
![]() ,
и мы хотим найти
,
и мы хотим найти
![]() .
Разделим
.
Разделим
![]() на
на
![]() с остатком
с остатком
![]() ,
,
![]() .
Если
.
Если
![]() ,
то разделим
,
то разделим
![]() на
на
![]() :
:
![]() ,
,
![]() и т.д. Получим последовательность
равенств с убывающими остатками
и т.д. Получим последовательность
равенств с убывающими остатками
![]() :
:
|
|
|
(2) |
где
![]()
Если
![]() — последний ненулевой остаток, то
— последний ненулевой остаток, то
![]() .
Очевидно, что, в этом случае
.
Очевидно, что, в этом случае
![]() .
.
Процедура вычисления последовательности (2) называется алгоритмом Евклида.
Пример 5. Найти
![]() .
.
Решение:
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом![]() .
.
Для практического использования приведенного алгоритма важнейшим является вопрос о времени его выполнения.
Теорема 1. При
![]() алгоритм Евклида позволяет вычислить
алгоритм Евклида позволяет вычислить
![]() за время порядка
за время порядка
![]() .
.
Доказательство:
Во-первых, очевидно,
что остатки в алгоритме Евклида строго
уменьшаются с каждым шагом, и следовательно
достигнут в конце концов нуля. Чтобы
убедиться, что последний остаток есть
НОД, воспользуемся вторым определением
НОД. Получаем, что если некоторое число
делит и
![]() и
и
![]() ,
то оно должно делить и
,
то оно должно делить и
![]() .
А так как оно делит
.
А так как оно делит
![]() и
и
![]() ,
то оно должно делить
,
то оно должно делить
![]() и т.д. В конце концов, получаем, что оно
должно делить последний ненулевой
остаток. С другой стороны, переходя от
последнего шага к предыдущему, легко
видеть, что последний остаток должен
делить все предыдущие остатки, а также
и т.д. В конце концов, получаем, что оно
должно делить последний ненулевой
остаток. С другой стороны, переходя от
последнего шага к предыдущему, легко
видеть, что последний остаток должен
делить все предыдущие остатки, а также
![]() и
и
![]() .
Так это НОД, по второму определению.
.
Так это НОД, по второму определению.
Главный вопрос в данном случае состоит в том, сколько раз производится деление.
Лемма:
![]() .
.
Доказательство:
Если
![]() ,
то сразу получаем
,
то сразу получаем
![]() .
Пусть теперь
.
Пусть теперь
![]() .
В этом случае следующее деление дает
.
В этом случае следующее деление дает
![]() и
и
![]() .
Ч.т.д.
.
Ч.т.д.
Таким образом мы
убедились, что за каждые два шага
алгоритма остаток уменьшается, по
крайней мере, вдвое [3]. Таким образом,
результат работы алгоритма достигается
не позднее чем через
![]() делений чисел разрядностью, не
превосходящих
делений чисел разрядностью, не
превосходящих
![]() каждое. Отсюда получаем искомую оценку
времени.
каждое. Отсюда получаем искомую оценку
времени.
Теорема 2.
Наибольший
общий делитель
![]() двух чисел
двух чисел
![]() и
и
![]() ,
где
,
где
![]() ,
можно представить в виде линейной
комбинации этих чисел
,
можно представить в виде линейной
комбинации этих чисел
![]()
![]() с
целыми коэффициентами
с
целыми коэффициентами
![]() и
и
![]() ,
за время порядка
,
за время порядка
![]() .
.
Схема доказательства.
Для
доказательства теоремы достаточно
показать [2,3], что представление числа
![]() может быть найдено путем последовательного
выражения
может быть найдено путем последовательного
выражения
![]() через все более ранние остатки в алгоритме
Евклида, на что будет затрачено одно
умножение и одно сложение или вычитание.
Поскольку количество операций реализующих
сложение есть величина более низкого
порядка, то получаем искомую оценку
времени.
через все более ранние остатки в алгоритме
Евклида, на что будет затрачено одно
умножение и одно сложение или вычитание.
Поскольку количество операций реализующих
сложение есть величина более низкого
порядка, то получаем искомую оценку
времени.
Рассмотрим также расширенный алгоритм Евклида применяющийся для нахождения корней диофантова уравнения первой степени.
Дано:
![]() ,
,
![]() .
.
Требуется найти:
![]() ,
,
![]() и
и
![]() ,
такие что
,
такие что
![]() ,
где
,
где
![]()
Алгоритм:
1. Если b=0 положить d:=a, x:=1, y:=0 и возвратить (d,x,y)
2. Положить x2:=1, x1:=0, y2:=0, y1:=1
3. Пока b>0
3.1 q:=[a/b], r:=a-qb, x:=x2-qx1, y:=y2-qy1
3.2 a:=b, b:=r, x2:=x1, x1:=x, y2:=y1, y1:=y
4. Положить d:=a, x:=x2, y:=y2 и возвратить (d,x,y)
Замечание:
Расширенный алгоритм Евклида может быть применен для нахождения обратного значения по модулю. Для этого необходимо
1. Использовать расширенный алгоритм Евклида для нахождения
x и y, таких, что ax + ny = d, где d=НОД(a,n).
2. Если d > 1, то обратного элемента не существует.
Иначе возвращаем x.
Определение 10.
Два целых
числа
![]() и
и
![]() называются взаимно простыми, если
называются взаимно простыми, если
![]() ,
т.е. если они не имеют общих делителей
больших
,
т.е. если они не имеют общих делителей
больших
![]() .
.
Определение
11. Для любого
целого положительного числа
![]() функция Эйлера
функция Эйлера
![]() определяется как число неотрицательных
целых
определяется как число неотрицательных
целых
![]() ,
меньших
,
меньших
![]() и взаимно простых с
и взаимно простых с
![]() :
:
|
|
|
|
Из определения следуют следующие свойства функции Эйлера:
1.
![]() .
.
2. Для любого
простого
![]()
|
|
|
|
Несложно показать,
что для любого простого
![]() и некоторого
и некоторого
![]()
|
|
|
|

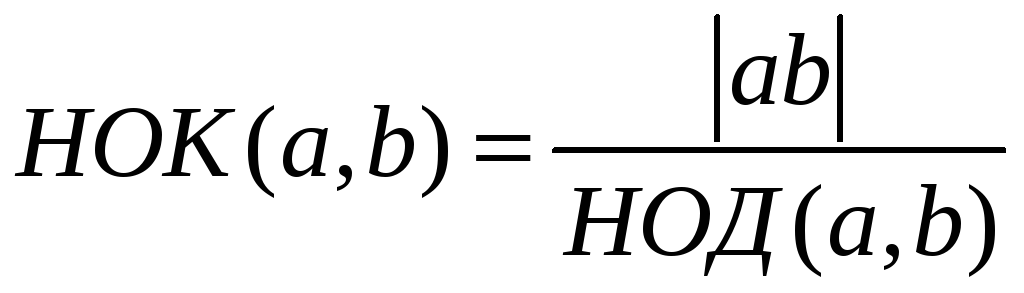 .
. .
.