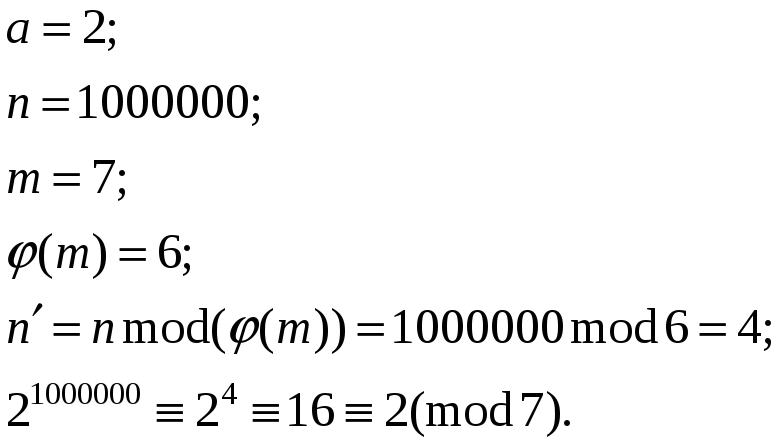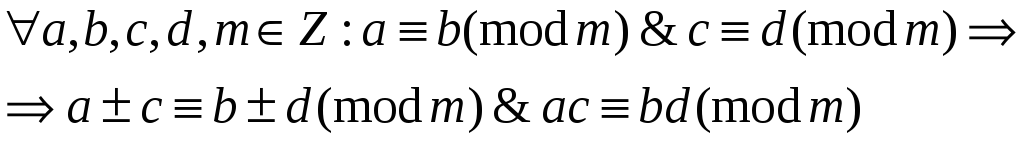ММЗИ / Лекции / Сравнения

2. Сравнения

Определение 1. Для данных целых чисел , и , говорят, что сравнимо с по модулю , если разность делится на :

.

При этом число называется модулем сравнения.

Из определения 1 непосредственно следуют следующие свойства сравнений:

1. Рефлексивность:

.

2. Симметричность:

.

3. Транзитивность:

.

Таким образом, для фиксированного значения отношение сравнимости является отношением рефлексивным, симметричным и транзитивным, т.е. отношением эквивалентности.

В этих условиях каждый класс эквивалентности по этому отношению обладает в точности одним представителем в множестве чисел от до [3-5]. Иными словами, любое целое число сравнимо по модулю ровно с одним числом в промежутке от до .

Множество классов эквивалентности по модулю (называемых классами вычетов) обозначается .

Несложно убедиться, что сравнения обладают следующим свойством.

4. Коммутативность

Таким образом, множество является коммутативным кольцом, т.е. классы вычетов по одному и тому же модулю можно складывать, вычитать и перемножать, и эти операции удовлетворяют обычным аксиомам ассоциативности, коммутативности, существования противоположного элемента и т.д.

Рассмотрим условия существования противоположного элемента.

Теорема 1. Для каждого целого существует единственное целое число , такое что произведение сравнимо с по модулю , тогда и только тогда, когда и − взаимно просты:

.

Схема доказательства: Для доказательства теоремы необходимо представить в виде и воспользоваться теоремой 2 и свойствами сравнений [3].

Следствие: Если то обратный элемент (из условия ) может быть найден за время двоичных операций.

Замечание: Если , то под отрицательной степенью подразумевается -я степень обратного класса вычетов, т.е. класс вычетов, содержащий -ю степень любого целого числа , такого, что .

Подробное рассмотрение свойств сравнений позволяет получить следующий важный результат.

Теорема 2 (малая теорема Ферма). Пусть − простое число. Любое целое число удовлетворяет сравнению , и любое целое число , не делящееся на , удовлетворяет сравнению .

Из условий данной теоремы несложно получить следствие.

Следствие. Если не делится на и если , то .

Доказательство. Т.к. p–1| n–m, что следует из свойств сравнений, то для некоторого положительного «c» получаем n = m+c*(p–1). Умножая почленно a^p–1  1(mod p) и сравнение a^m  aⁿ (mod p), получаем

aⁿ  a^m (mod p).

Пример 6. Найти последнюю цифру в записи числа в системе счисления по основанию 7.

Решение: Пусть , т.к. , то

. Следовательно, последняя цифра равна 2.

Не менее важное свойство сравнений отражает т.н. китайская теорема об остатках.

Теорема 3 (китайская теорема об остатках). Пусть требуется решить систему сравнений по различным модулям:

причем любые два модуля сравнения взаимно просты относительно друг друга: . Тогда эта система разрешима, и любые два решения сравнимы по модулю .

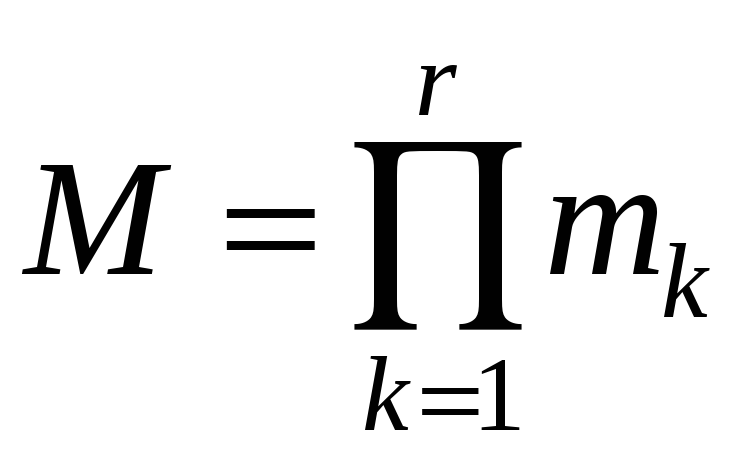Данная теорема позволяет сформулировать следующее важное следствие.

Следствие. Функция Эйлера обладает свойством «мультипликативности», т.е.

.

Теорема 4. Пусть известно, что есть произведение двух простых чисел и . Тогда зная эти числа и , можно найти за время порядка и обратно, зная и , можно найти и за время порядка .

Доказательство. Утверждение очевидно, если − четно, т.к. в этом случае , и ; поэтому рассмотрим случай когда − нечетно. В силу мультипликативности функции Эйлера для получаем . Таким образом, значение может быть получено с помощью одного сложения и одного вычитания.

Обратно, предположим, что известны и , и требуется найти и . Для неизвестных величин и известны их произведение и сумма . Обозначим последнее выражение через (отметим, — число четное). Но два числа, произведение которых равно , а сумма , по теореме Виета должны быть корнями квадратного уравнения . Итак и равно . Наибольшее время при вычислении занимает процедура извлечения квадратного корня: на нее требуется двоичных операций [3].

Рассмотрим обобщение малой теоремы Ферма, сделанное Эйлером.

Теорема 5 (теорема Эйлера).

.

Схема доказательства. Для начала необходимо доказать справедливость утверждения для случая, когда есть степень простого числа: . Выполняя индукцию по , при , получаем малую терему Ферма. Рассматривая биномиальные коэффициенты в выражении , получаем доказательство частного случая.

В дальнейшем, используя мультипликативность функции Эйлера и тот факт, что степени различных простых чисел взаимно просты, доказывается и общий случай [6-8].

Следствие. Если и — наименьший неотрицательный вычет по модулю , то .

Пример 7. Вычислить .

Решение: