ММЗИ / Лекции / Возведение вычетов в степень методом повторного возведения в квадрат

Возведение вычетов в степень методом повторного возведения в квадрат

Основным действием, которое наиболее часто приходится выполнять в модулярной арифметики является отыскание значения .

Методы решения этой задачи позволяют получать ответ за конечное число шагов при различных временных затратах. Помимо тривиального метода непосредственного возведения в степень, существует более эффективные алгоритмы, основывающиеся на использовании китайской теоремы об остатках или теоремы Эйлера.

Существует и другой достаточно эффективный метод, основывающийся на мультипликативности вычетов и называемый методом повторного возведения в квадрат.

В дальнейшем будем предполагать, что b<m и что, вычислив произведение, мы его тут же приводим по модулю m. В таком случае во всех операциях мы будем оперировать величинами, не превышающими m².

В этих условиях рассмотрим следующую последовательность действий.

Используем символ a для обозначения промежуточного результата умножения. В конце работы алгоритма a примет значение наименьшего неотрицательного вычета .

В начале положим a=1. Пусть n₀ n₁ n₂…n_k-2 n_k-1 –цифры двоичной записи числа n.

То есть каждое n_j равно либо 1, либо 0.

Если n₀=1, заменим a на b, в противном случае оставим a=1.

Возведем b в квадрат: .

Если n₁=1, то умножаем a на b₁ и приводим его по модулю m

Возведем b₁ в квадрат: .

Если n₂=1, то умножаем a на b₂ и приводим его по модулю m

Продолжая в дальнейшем выполнять действия по приведенному правилу, на j-том шаге мы получим: . Если n_j=1, то есть если входит в двоичное представление числа n, используем b_j как множитель для вычисления нового значения a и не делаем этого при n_j=0.

Легко убедится, что после k-1 шага получим . Причем общее число шагов, необходимых для работы алгоритма k-1.

Справедлив вопрос о числе двоичных операций, необходимых для решения поставленной задачи с использованием данного алгоритма.

На каждом шаге мы проводили одно или два умножения для чисел, не превосходящих значения m². При общем числе шагов К-1 и числе двоичных операций на каждом шаге

O(log²m²)=O(log²m)

получаем следующую оценку.

Теорема 1.

Time(bⁿ mod m) = O((logⁿ)(log²m))

Рассмотрим вопрос о мультипликативность функции Эйлера, получим следующие достаточно важный результат.

Теорема 2.

Сумма функций Эйлера всех чисел d – делителей числа n.

Доказательство.

Обозначим через f(n) левую часть этого равенства. Требуется доказать, что f(n)=n. Покажем сначала, что функция f(n) мультипликативная, т.е.

f(m*n) = f(m) * f(n) <=> НОД(m, n) = 1

Заметим, что любой делитель d числа mn может быть единственным образом представлен в виде произведения d = d₁ * d₂, где d₁|m d₂|n

Т.к. НОД(d₁, d₂) = 1, то φ(d_1* d₂) = φ(d₁) * φ(d₂)

в силу мультипликативности функции Эйлера.

Таким образом получаем все возможные делители d числа mn, взяв все возможные делители d₁ и d₂ чисел m и n соответственно.

Таким образом

f(m * n) =

делители мультипликативные.

Теперь для доказательства теоремы предположим n = p₁^α1 * p₂^α2 * … * p_r^αr есть разложение на простые множители.

Так как f – функция мультипликативная, то f(n) = Πf(p_i^αi) ,

Поэтому достаточно доказать наше предположение для чисел p^α, т.е. доказать, что f(p^α) = p^α

Т.к. все делители числа p^α имеют вид p^j , получаем

,

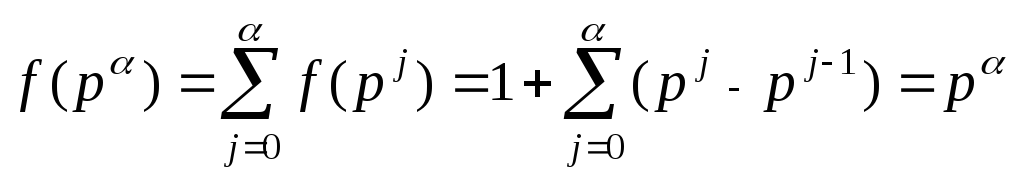что доказывает справедливость теоремы.