МСТВ тестирование - ошибки и ответы

16. В первой урне 3 черных шара и 7 белых шаров. Во второй урне 4 белых шара и 5 черных шаров. Из первой урны переложили один шар во вторую урну. Тогда вероятность того, что шар, вынутый наудачу из второй урны, будет белым, равна …

			0,47
			0,55
			0,35
			0,50

Решение: Для вычисления вероятности события A (вынутый наудачу шар – белый) применим формулу полной вероятности: . Здесь – вероятность того, что из первой урны переложили во вторую урну белый шар; – вероятность того, что из первой урны переложили во вторую урну черный шар; – условная вероятность того, что вынутый шар белый, если из первой урны во вторую был переложен белый шар; – условная вероятность того, что вынутый шар белый, если из первой урны во вторую был переложен черный шар. Тогда .

17. Дискретная случайная величина X задана законом распределения вероятностей: Тогда ее среднее квадратическое отклонение равно …

			0,80
			0,64
			2,60
			14,16

Решение: Среднее квадратическое отклонение случайной величины определяется как , где дисперсию дискретной случайной величины можно вычислить по формуле . Тогда , а .

18. Статистическое распределение выборки имеет вид Тогда значение относительной частоты 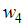равно …

			0,25
			0,05
			0,26
			0,75

Решение: Сумма относительных частот равна единице. Поэтому .

19. Проведено пять измерений (без систематических ошибок) некоторой случайной величины (в мм): 4,5; 5,2; 6,1; 7,8, 8,3. Тогда несмещенная оценка математического ожидания равна …

			6,38
			6,42
			6,1
			6,4

Решение: Несмещенная оценка математического ожидания вычисляется по формуле 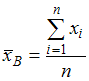. То есть .

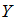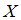20. Выборочное уравнение прямой линии регрессии на имеет вид . Тогда выборочный коэффициент регрессии равен …

			– 1,5
			1,5
			4

Решение: Если выборочное уравнение парной регрессии имеет вид , то выборочный коэффициент регрессии равен . То есть .

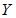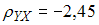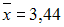21. При построении выборочного уравнения прямой линии регрессии на вычислены выборочный коэффициент регрессии , и выборочные средние и 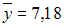. Тогда уравнение регрессии примет вид …

Решение. Выборочное уравнение прямой линии регрессии на имеет вид . Тогда , или .

22. При построении выборочного уравнения парной регрессии вычислены выборочный коэффициент корреляции 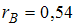и выборочные средние квадратические отклонения 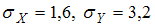. Тогда выборочный коэффициент регрессии Y на X равен …

Решение: Выборочный коэффициент регрессии Y на X вычисляется по формуле . Тогда .