
- •Автоматизация обработки информации об обстановке
- •Первичная обработка радиолокационной информации
- •Автоматическая завязка траектории целей.
- •Автоматическое сопровождение целей
- •2.6 Стробирование и селекция отметок целей при обработке информации о воздушной обстановке
- •Допустимые значения суммарного эллиптического отклонения
- •Сбор и обобщение данных о воздушной обстановке
- •Ошибки расчета координат целей
- •Алгоритмы обработки информации о постановщиках помех
- •Значение ω рассчитывается по формуле
2.6 Стробирование и селекция отметок целей при обработке информации о воздушной обстановке
Из описания алгоритмов сопровождения траекторий целей видно что обработка информации о воздушной обстановке является весьма трудоемким процессом, требующим больших затрат оперативной памяти и быстродействия ЭВМ АСУ.
Одной из основных операций, выполняемых в процессе формирования информационной модели обстановки, является отбор отметок целей из числа полученных в последнем цикле работы источника для продолжения каждой из сопровождаемых траекторий. Отбор отметок последующей их "привязкой" к сопровождаемым целям принято называть селекцией траекторий.
Селекцияпроводится путем сопоставления вероятностей принадлежности вновь полученных отметок к сопровождаемой цели. К траектории привязывается та отметка, которая имеет наибольшую вероятность принадлежности к данной цели. Однако так как непосредственное определение значений этих вероятностей связано с существенными трудностями, то для упрощения процесса селекции отбор и при вязка отметок производятся на основе сравнения координат и параметров движения целей, полученных в очередном обзоре, с расчетными экстраполированными.) координатами и характеристиками сопровождаемых траекторий.В простейшем случае селекция осуществляется только по координатам отметок.
В процессе селекции принято выделять два последовательно выполняемых и взаимно связанных этапа - стробирование отметок и селекция отметок в стробе (сличение информации).
Стробированиезаключается в выделении области, в которой с некоторой вероятностью ожидается появление цели, и регистрации всех попадающих в эту область отметок. Формально в качестве тамгой области может быть выбрана вся гона обзора РЛС. Но в этом случае значительно возрастает объем вычислений, связанных с необходимостью сравнивать по всей зоне обзора координаты экстраполированных и реально наблюдаемых отметок целей. С целью сокращения объема вычислений селекция отметок обычно производится в стробах.
Строб представляет собой заранее выбранную область зоны обзора станции разведки, координаты центов которой совпадают с координатами экстраполированной отметкеРазмеры, форма и ориентация строба существенно влияют на качество сопровождения траекторий. Вид и размеры строба определяются на основе статистических данных о точностных характеристиках источников информации, ошибок обработки информации в АСУ и маневренных возможностях целей. При этом должны обеспечиваться требуемые знания показателей качества сопровождения (например надежности сопровождения, разрешающей способности системы сопровождения, вероятности правильной селекции и др.) При слежении за несколькими целями или при работе в условиях помех в строб может попасть несколько отметок, на которых только одна в действительности принадлежит сопровождаемой цели (остальные либо образованы помехами, либо относятся к соседним целям). Поэтому при вторичной обработке информации возникает необходимо иметь селекции отметок в стробе с целью выбора из всех попавших в строб отметок той одной, вероятность принадлежности которой сопровождаемой трассе максимальна.
Стробирование отметок. Используемые в настоящее время методы стробирования отметок принято разделять на физические и математические.
Сущность физического стробирования состоит в выделении области вероятного появления новой отметки сопровождаемой цели путем непосредственного воздействия на приемное устройство Р.1С (например, отпирания его только в областях предполагаемого появления отметки.)
Под математическим стробированием понимается способ формирования области вероятного появления новой отметки в виде некоторой совокупности чисел (системы неравенств), аналогично определяют Щ11Х граница строба. При обработке информации в АСУ осуществляется, как правило, математическое стробирование. В дальнейшем рассматриваются только эти методы стробирования.
Форма строба зависит от вида используемой при обработке информации системы координат в АСУ выбрана прямоугольная система, то наиболее простым для машинной реализации являютсяпрямоугольный строб (здесь и в Последующем рассматривается стробирование на плоскости). Прямоугольные стробы могут задаваться либо координатами центра стробаХэт,Yэти величинами допустимых отклонений относительно центра ΔХс, ΔYc, либо координатамиХн,YниХк,Yк, определяющими границы строба (рис.2.17). Более удобным для реализации в алгоритмах ВОИ, базирующихся на полуавтоматическом или комбинированном методах сопровождения, является первый способ представления стробов.
При обработке информации в сферической системе координат простейший строб задается либо координатами центра строба βэт, Dэти его размерами относительно центра Δβс, ΔDcС, либо координатами границ строба βн, βкпо азимуту иDн,Dкпо дальности (рис.2.17).
У
Рис. 2.17. Способы
представления стробов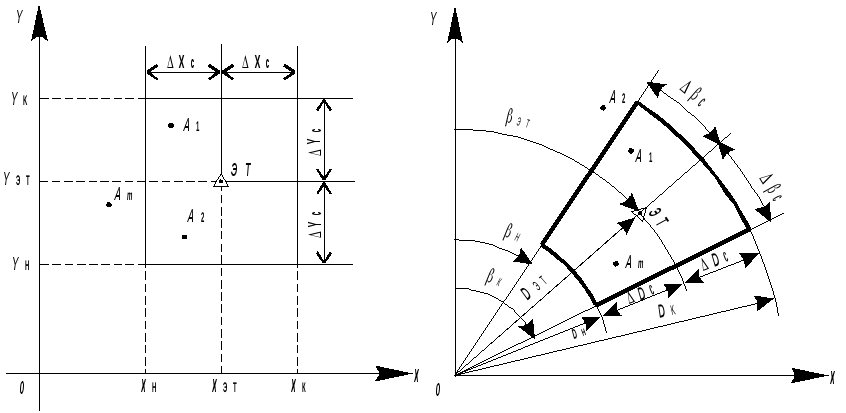
![]() ,
,
![]() ,
,
для прямоугольной системы координат и (2.23)
![]()
![]() Dи–Dэт
Dи–Dэт![]()
![]()
при работе в сферической системе координат.
В выражении (2.23)
Хи,Yи,
![]() и,
Dи
есть измеренные значения координат
наблюдаемых отметок (А1, А2.-.Аnна рис.2.17).
и,
Dи
есть измеренные значения координат
наблюдаемых отметок (А1, А2.-.Аnна рис.2.17).
Размеры стробов выбираются из условия обеспечения заданной, вероятности попадания в площадь строба Sреальной отметки сопровождаемой цели. Эта вероятностьРц(S) выражается зависимостью
РЦ(S)
-![]() (2.24.)
(2.24.)
где δ -рассеивание наблюдаемых отметокХи,Уиотносительно экстраполированной точки ЭТ с координатамиXэт,Yэт;
W(δ) - плотность распределения вероятностей рассеивания отметок
цели относительно ЭТ.
Чем больших размеров выбран строб, там, естественно, выше вероятность Рц(S). Так, например, если выбрать прямоугольный строб с размерами ΔХc-δΔxи ΔYc-δΔy, где δΔxи δΔy- суммарные средние квадратические отклонения наблюдаемых отметок от экстраполированных, то при нормальном, распределении ошибок измерения и экстраполяции вероятность попадания отметки цели в строб равна 0,68. Для получения вероятностиРц(S), близкой к единице, необходимо,пользуясь правилом "трех сигм", брать размеры строба разными ΔХс - 3бΔх , ΔYс - ЗбΔy .
Однако вместе с увеличением размеров строба увеличивается и вероятность попадания в него ложных отметок
![]()
где Wμ (δ) - плотность распределения вероятности ложных отметок в зоне наблюдения.
Таким образом, при выборе размеров строба возникает противоречивая ситуация: стремление увеличить вероятность попадания реальной отметки в строб ведет к возрастанию вероятности попадания в него ложных отметок. Это противоречие разрешается путем отыскания оптимального по размерам строба.
Одним из необходимых условий решения данной задачи является определение статистических характеристик рассеивания наблюдаемых отметок А относительно центра строба ЭТ (рис 2.18). Полными статистическими характеристиками величины δ являются плотности распределения вероятности рассеивания реальных отметок Wц(δ) и ложных отметокWμ(δ) относительно ЭТ (в общем случае отметки А могут принадлежать как реальным, так и ложным трассам).
Выражения для плотностей распределения Wц(δ) иWμ(δ) находятся следующим образом. Величины отклонений связаны с прямоугольными составляющими ΔХи ΔУизвестным соотношением
![]()
где ΔХ=Хи-Хэт, ΔY=Yи-Yэт.
Следовательно, одновременные плотности распределения Wц(σ) иWμ(σ) могут быть заменены двумернымиWц(ΔX,ΔY), Wμ(ΔX,ΔY).
Отклонения ΔX и ΔYявляются случайными величинами и могут быть представлены в виде суммы абсолютных ошибок измерения(схема) координат цели ΔXи, ΔYи и ошибок экстраполяции ΔXэ,ΔYэ (рис. 2.18):
ΔX=ΔХи+ΔXэ,
Δ
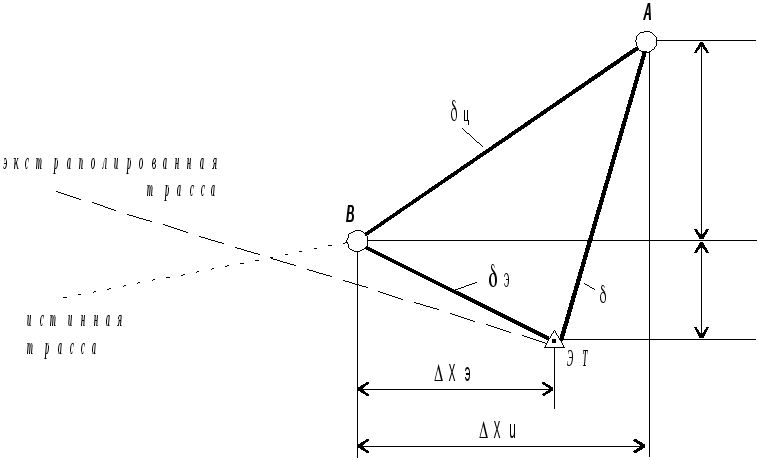 Рис.
2.18.К определению величины рассеивания
.
Рис.
2.18.К определению величины рассеивания
.
Обычно предполагается, что ошибки измерения и экстраполяат координат подчиняются нормальному закону распределения с математическими ожиданиями равными нулю. Тогда, согласно теореме с композиции нормальных распределений, величины ΔX и ΔYтакже распределяются нормально с математическими ожиданиямиmΔx-mΔy=0 и дисперсиямиδ2 Δx,δ2Δy.
Так как корреляция между отклонениями ΔX и ΔY практически отсутствует, то выражение для двумерной плотности распределения рассеивания отметок реальной цели относительно центра строба имеет вид:
![]() ехр
ехр![]()
![]() ,
(2. 26)
,
(2. 26)
Ложные отметки статистически могут быть охарактеризованы средней плотностью появления отметок во времени. Более наглядны и удобной для использования характеристикой является средняя плотность количества ложных отметок μ, приходящихся на единицу площади зоны наблюдения за один обзор РЛС
![]() ,
,
где ε - средняя плотность появления ложных отметок во времени (отм/с);
S-площадь зоны наблюдения (м);
То- период обзора РЛС(с).
При исследовании алгоритмов ВОИ принято полагать, что ложные отметки появляются случайно и независимо во всей зоне наблюдения S и распределены по закону равномерной плотности. При таких условиях плотность распределения вероятности рассеивания ложных отметок приближенно равна
![]() (2.27),
(2.27),
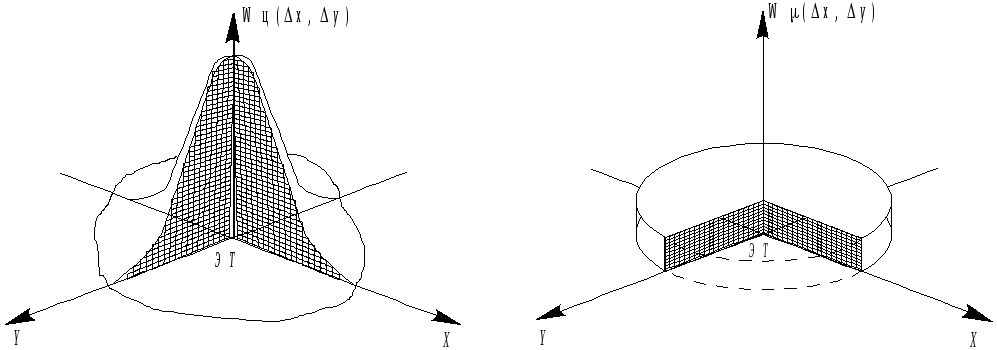
На рис.2.19 представлены поверхности распределения, отображающие функции Wц(ΔX,ΔY) Wμ(ΔX,ΔY) Как следует из выражений (2.26), (2.27) и графиков, приведенных на рис.2.19, характер распределения реальных и ложных отметок относительно центра строба существенно различен. Плотность вероятности появления реальной отметки увеличивается с приближением к центру строба и достигает максимума в точке ЭТ. Распределение ложных отметок в пределах строба остается равномерным. На этих отличиях в статистических закономерностях отметок основываются алгоритмы стробирования и селекции целей при ВОИ. Существенное влияние на размеры стробов оказывает характер
движения цели и используемый в системе сопровождения алгоритм обработки информации. При отсутствии маневра цели и используемый в системе сопровождения алгоритм обработки информации. При отсутствии маневра цели и при вычислении экстраполированных координат по достаточно большому количеству наблюдаемых отметок размеры строба ΔXс, ΔYс могут быть сделаны минимальными, так как они определяются главным образом ошибками измерения координат δXи, δYи
П
Рис. 2.19. Характер
распределения реальных и ложных отметок.
Кроме того, качество ВОИ в сильной мере зависит от стабильности и периодичности поступления реальных отметок на вход системы сопровождения. Так, при пропуске одной или нескольких отметок подряд вычисление координат центров стробов ведется по предыдущим значениям координат и скорости цели. Ошибки экстраполяции при этом резко возрастают.
Следовательно, для обеспечения высокого качества ВОИ в алгоритмах обнаружения и сопровождения траекторий целей должна быть предусмотрена возможность формирования стробов нескольких размеров:
малого стро6а для сопровождения неманеврирующих или слабо маневрирующих целей при отсутствии пропусков отметок;
среднего строба для обнаружения и сопровождения траекторий маневрирующих целей при отсутствии пропусков отметок;
большого строба для обнаружения и сопровождения маневрирующих целей при наличии пропусков отметок.
В любом из выбранных на основе приведенных выше соображений стробов возможно попадание ложных отметок образованных искусственными помехами и внутренними шумами РЛС и автомата ПОИ.
Д
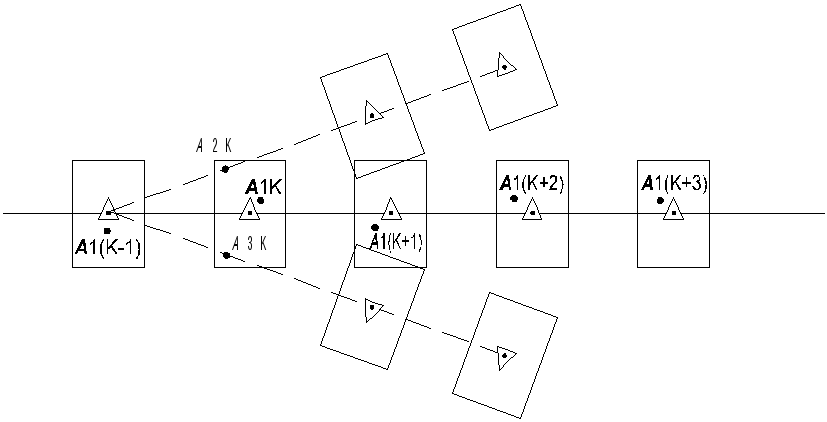 Рис.
2.20. К пояснению способов продолжения
траектории.
Рис.
2.20. К пояснению способов продолжения
траектории.
Алгоритмы селекции отметок в стробах.
При решении задачи селекции отметок могут быть использованы два способа продолжения траектории сопровождаемой цели. Оба способа базируются на статистических различиях в вагонах движения реальных и ложных целей.
Суть первого способа состоит в том, что траектория продолжается по каждой из попавшей в строб отметок (рис.2.2О). Это приводит к "разветвлению" траектории, причем часть ее ветвей являются ложными (на рис.2.20 они показаны пунктиром). Однако ответвления траектории, построенные по ложным отметкам, вскоре должны быть сброшены с сопровождения из-за отсутствия корреляции между такими метками в последующих обзорах РЛС. Траектория же, построенная по реальным отметкам (точки А1(к-1), А1к, А1(к+2) на рис.2.20), будет продолжена. Данному способу селекции отметок присущи существенные недостатки: в связи с необходимостью сопровождать, хотя и кратковременно, ложные цели значительно повышаются требования к производительности ЦВМ ВОИ; "засорение" индикаторных устройств пунктов управления трассами ложных целей резко увеличивает психологическую нагрузку на боевой расчет АСУ.
При втором способе из всех отметок, попавших в строб, выбирается одна, вероятность принадлежности которой к сопровождаемой траектории наибольшая. Остальные отметки отбрасываются как ложные. Так как на практике чаще применяется второй способ продолжения траекторий, то в дальнейшем рассматриваются методы селекции отметок в стробах, основанные на этом подходе.
По своей сущности задача селекции отметок представляет задачу проверки двух взаимно исключающих гипотез НоиН1для каждой изqпопавших в строб отметок. ГипотезаНосостоит в том, чтоj-я отметка, отклонения координат которой от центра строба равны ΔXj, ΔYj (j-1,q), является ложной. Альтернативная ей гипотезаН1состоит в том, чтоj-я отметка принадлежит сопровождаемой цели. В Результате проверки гипотез по всемq отметкам должно быть принято решение о том, какую из отметок следует считать продолжением траектории.
Если известны функции правдоподобия L(ΔXj, ΔYj /Н1) иL(ΔXj, ΔYj /Но), то решение задачи селекции отметок сводится к испытанию отношения правдоподобия λ(Х), то есть к проверке условия:
![]() (2. 28).
(2. 28).
Пороговое значение φ может быть выбрано в соответствии с одним из известных методов принятия статистических решений, например, исходя из нежелательности попадания ложных отметок в строб, или, что то же самое, из условия достижения минимума ошибки принятия решения о принадлежностиj-й отметки к сопровождаемой трасе, когда на самом деле отметка является ложной (критерий Найма - Пирсона).
При высказанном выше смысловом содержании гипотез Н1иНоотношение функций правдоподобия отклонений реальных и ложных отметокL(ΔXj, ΔYj /Н1) и L(ΔXj, ΔYj /Но) характеризуется отношением плотностей распределенияWц(ΔXj,ΔYj) Wμ(ΔXj,ΔYj) Тогда отношение (2.28) может быть записано в виде:
![]() (2.29).
(2.29).
Подставив выражение для плотностей вероятностей (2.26) и (2.27) в отношение (2.29), получим
![]() ехр
ехр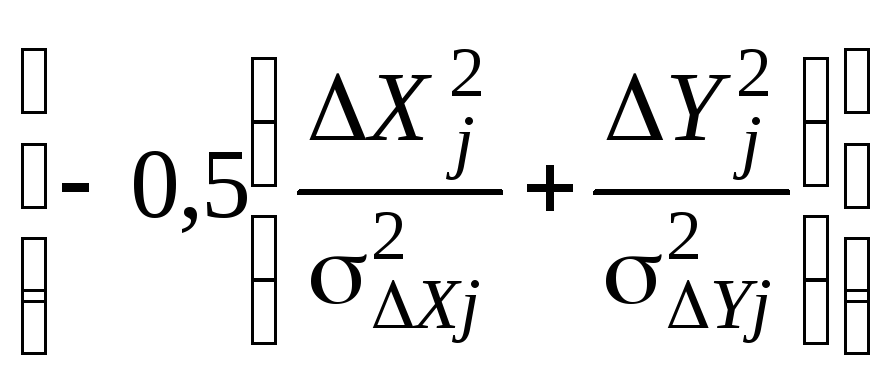
![]() (2.30).
(2.30).
Проанализировав соотношение (2.30), можно сделать важный для дальнейшего изложения вывод: при известных (фиксированных) значениях ошибок измерения и экстраполяции координат сопровождаемых целей δΔx, δΔyи заданной средней плотности ложных отметок для максимизации отношения правдоподобия необходимо минимизировать величину
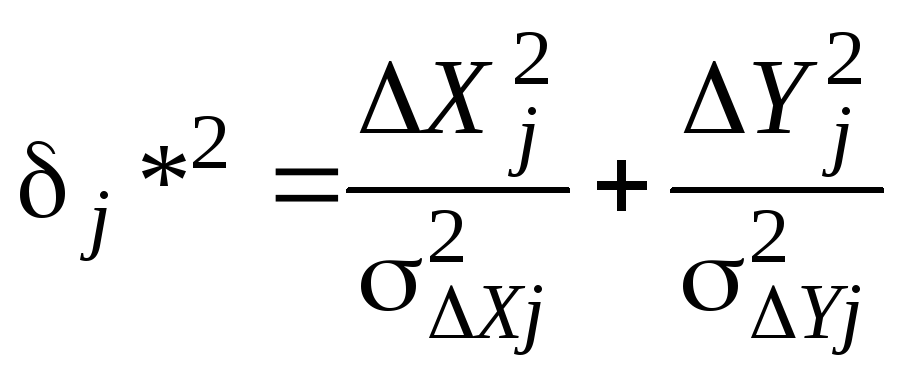 (2.31).
(2.31).
Данное выражение представляет собой уравнение эллипса равных вероятностей (эллипса рассеивания), центр которого совпадает с центром строба. Поэтому отклонения отметок от центра строба σ*j, принято называть суммарными эллиптическими отклонениями. Эллипс рассеивания сориентирован таким образом, что направление одной главной оси рассеивания совпадает с экстраполированной трассой (прямаяММ1), а вторая ось перпендикулярна этому направлению (рис.2.21).
Л
Рис. 2.21. Эллипс равных вероятностей.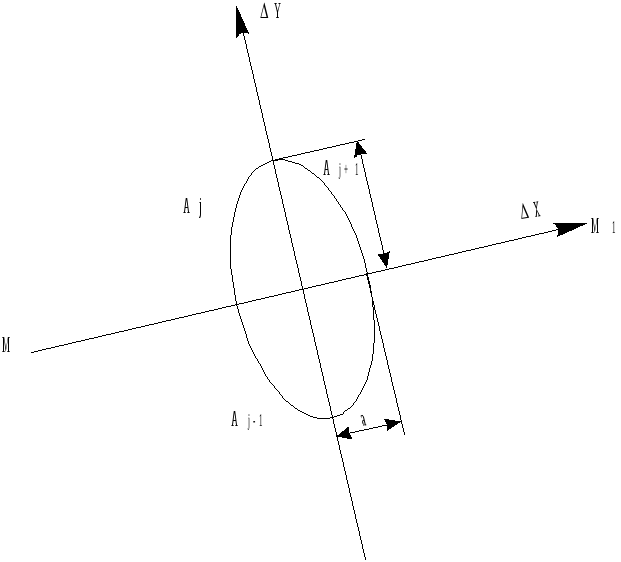
Метод минимальных эллиптических отклонений.
Данный метод является одним из общих методов селекции траекторий целей, позволявшим учитывать влияние на качество ВОИ таких факторов, как вид совершаемого целью маневра, наличие пропусков отметок в зоне наблюдения в предшествующих циклах наблюдения, ошибки съема координат целей. Селекция отметок осуществляется в стробе эллиптической формы, координаты центра и размеры которого определяются по результатам обработки информации в nпредыдущих циклах работы источника информации (обзорах РЛС). Процесс отбора отметки, принадлежащей сопровождаемой цели, разделяется на несколько последовательно выполняемых операций (блок-схема алгоритма стробирования и селекции отметок в стробе методом минимальных эллиптических отклонений представлена на рис. (2.22).
Определение размеров и формирование оптимального строба (блоки 1, 2, 3).
После поступления на вход алгоритма селекции измеренных значений координат отметки Хиj,Уиj, полученных вk-м обзоре РЛС, учета дополнительных данных определяются средние квадратические отклонения координатj-й сопровождаемой цели,δ Δx, δ Δyот центр строба.
По полученным значениям δ Δx, δ Δy, при известных величинах средней плотности ложных отметок μ и порогового значения φ определяются размеры "оптимального" строба, то есть строба, значений которого в процессе селекции гарантирует выполнение требований о том, чтобы значение вероятности принятия о принадлежности ложной отметки к сопровождаемой траектории не превышало заданного уровня. Размеры оптимального строба характеризуются (рис.2.21) величиной полуосей
a=σ*доп δ Δxj иb= σ*доп δ Δyj,
где σ*доп -допустимое значение суммарного эллиптического отклонения.
3нание σ*доп позволяет ограничить пределы строба и в дальнейшем сформулировать условие попадания селектируемых отметокХиj Уиjв площадь оптимального строба.
Напомним, что значение σ*доп определяет и величину вероятности попаданий отметки в эллипс рассеивания
P[(Xj, Yj)S],
р
Рис.
2.22. Алгоритм селекции отметок целей
методом минимальных эллиптических
отклонений.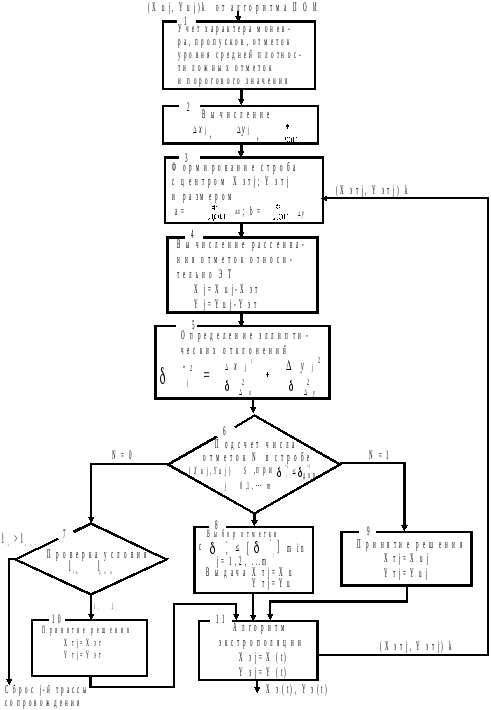
![]() (2.32).
(2.32).
В таб. 2.3 приведены некоторые наиболее часто используемые на практике величины функции (2.32) и соответствующими им значения σ*доп .
Величина σ*доп находиться их выражения (2.32) в предположении что заданный уровень вероятности правильной селекции достигается уже при равенстве отношения правдоподобияWц(ΔXj,ΔYj)/Wμ(ΔXj,ΔYj) порогового значения φ, то есть из равенства
![]() (2.33)
(2.33)
Таблица 2.2
