Тема 6. Показатели вариации

«Всякая вещь есть форма проявления беспредельного разнообразия»

Козьма Прутков, Плоды раздумья

План лекции

1. Абсолютные показатели вариации

2. Относительные показатели вариации

3. Меры вариации для сгруппированных данных

4. Правило сложения дисперсий

5. Вариация альтернативного признака

В социально-экономическом анализе важно знать не только среднее (или серединное) значение признака, но на сколько равномерно распределены эти значения относительно среднего значения. Поясним сказанное. Пусть заданы два вариационных ряда.

Ряд I: 1, 2, 3, 4, 5, 6, 6, 7, 8, 9, 10, 11

Ряд II: 4, 5, 5, 5,6, 6, 6, 6, 7, 7, 7, 8

Рассчитаем для этих рядов среднюю арифметическую, моду и медиану.

Ряд I. .

Ряд II. .

Оба ряда имеют одинаковое число наблюдений n=12 и имеют одинаковые значения средней арифметической, медианы и моды - все равные 6. Но мы ясно видим, что ряды различны. В чем же состоит суть различий между ними?

Рис.1. Сравнение вариации рядов I и II

Рисунок 1 графически изображает ряд I и ряд II.

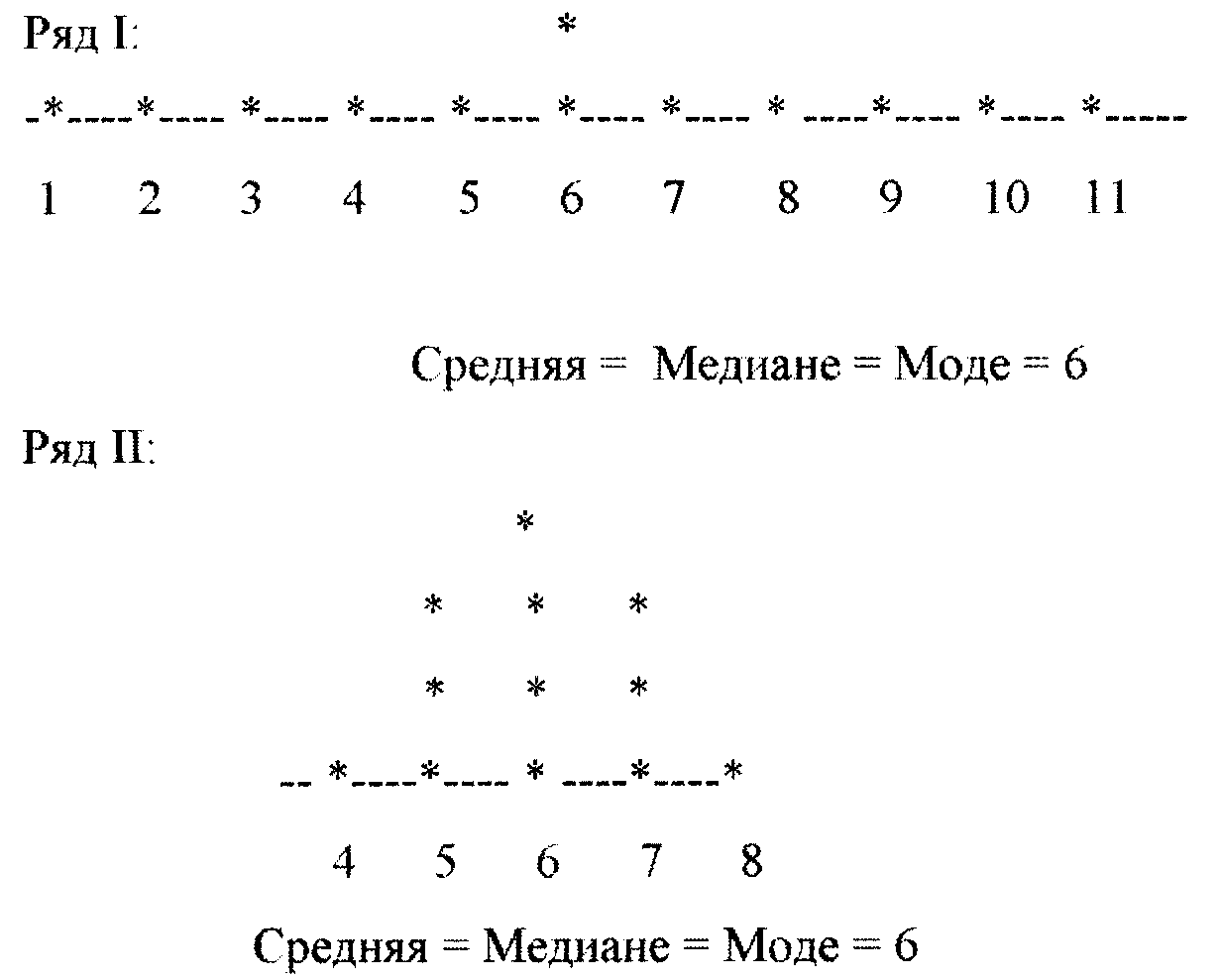
Оба ряда имеют одинаковые среднюю арифметическую, моду и медиану. Однако значения признака в первом ряду более широко разбросаны: они лежат дальше от средней по сравнению со вторым рядом, то есть вариация признака в первом ряду значительнее, чем во втором. Ряд I более вариабелен, чем ряд II.

В статистике используется ряд мер вариабельности (колеблемости). Наиболее простые из них: Интерквартильный размах – разница между первым и третьим квартилями. Чем больше величина интерквартильного размаха, тем больше рассеяние признака. Интерквартильный размах в ряду I равен 5.5, интерквартильный размах в ряду II равен 2. Размах вариации - разность между наибольшим и наименьшим значениями признака. Записывается: .Размах вариации в первом ряду равен 10. Размах вариации во втором ряду равен 4. Размах вариации и интерквартильный размах - меры разброса признаков в наборе данных. В первом ряду разброс выше, чем во втором. Недостаток этих мер в том, что размах вариации содержит информацию только о расстоянии между наибольшим и наименьшим значениями, а интерквартильный размах содержит информацию только о разности между верхним и нижним квартилями. Интерквартильный размах - более устойчив к значениям крайних вариантов.

Существуют и другие более тонкие и чаще используемые меры вариации, которые, подобно средней, арифметической используют всю информацию, содержащуюся в вариационном ряду.

Мы можем определить вариацию как меру отклонений значений признаков вариационного ряда от центра ряда распределения - средней арифметической. Например, можно взять сумму отклонений значений каждого признака ряда от средней арифметической:

,

где n – число признаков ряда.

Однако, сумма отклонений всех вариантов от их средней арифметической, согласно свойству средней арифметической, всегда равна нулю.

Для нахождения меры вариации можно каждое отклонение от средней взять по абсолютному значению. Эта операция изменяет отрицательные знаки отклонений на положительные, и мера вариации в этом случае не равна нулю.

- среднее линейное отклонение, (1)

Для взвешенных вариант:

Другой способ избежать нулевой суммы при исчислении средней суммы отклонений индивидуальных значений признака от среднего арифметического – возвести в квадрат каждую разность:

- дисперсия, (2)

Для взвешенных вариант:

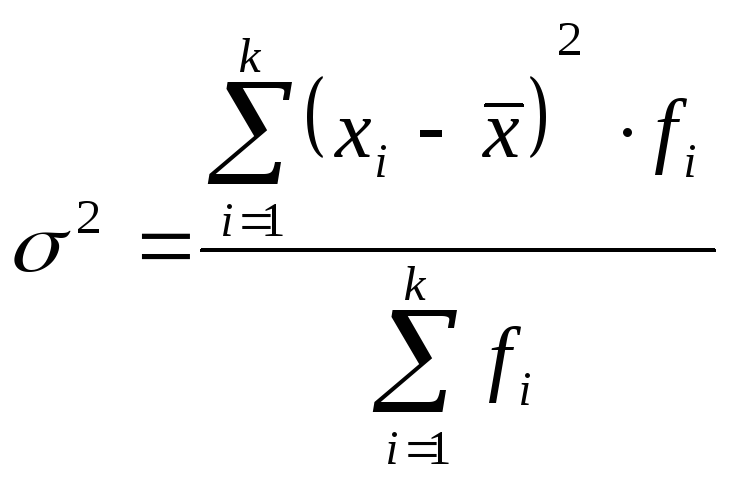
Дисперсия вариационного ряда есть средняя арифметическая квадрата отклонения (средний квадрат отклонения) значений признаков ряда от их средней арифметической.

(Поскольку  - греческая буква, то дисперсию часто просто называют сигма-квадрат, а заглавная греческая буква сигма  используется нами как символ, обозначающий суммирование)

Определим теперь стандартное отклонение (среднее квадратическое отклонение): Стандартное отклонение вариационного ряда есть арифметическое значение корня квадратного из дисперсии.



 = ² (3)

Для чего мы используем стандартное отклонение, если уже имеем такую меру вариации признаков как дисперсия? Желательно, чтобы показатель рассеяния выражался в тех же единицах измерения, что и значение признака (дисперсия этим свойством не обладает). Извлекая квадратный корень из дисперсии, мы получаем показатель, имеющий ту же единицу измерения, что и анализируемый признак.

В чем смысл дисперсии и среднего квадратического отклонения? Как мы можем интерпретировать их значения? По определению ² - средний квадрат отклонений вариантов от средней арифметической, это - мера рассеяния всех значений вариантов относительно средней арифметической. Чем больше вариация, тем дальше от средней находятся возможные значения признаков. Если сравнивают два вариационных ряда, то тот из них, который имеет большую дисперсию и среднее квадратическое отклонение, более вариабелен.

Риск, ассоциируемый с инвестициями, часто измеряют стандартным отклонением возврата инвестиций. Если сравниваются два типа инвестиций с одинаковой ожидаемой средней возврата, то инвестиции с более высоким средним квадратическим отклонением считаются более рискованными (хотя более высокое стандартное отклонение предполагает возврат более вариабельный с обеих сторон - как ниже, так и выше средней).

В научном анализе предпочтительно использование дисперсии, так как она имеет ряд полезных математических свойств, на практике же лучше работать со стандартным отклонением, поскольку эта мера легко интерпретируется.

Для ручного счета лучше пользоваться формулой дисперсии следующего вида, которая легко выводится из формулы (2)

 

² = х² - (х)² (4).