
Измерение тесноты связи в случае корреляционной зависимости.
Большинство
методов измерения тесноты связи
заключается в сопоставлении отклонений
значений признаков от их средних. Это
основано на предположении, что при
полной независимости признаков отклонения
значений факторного признака от средней
![]() носят случайный характер и должны
случайно сочетаться с различными
отклонениями
носят случайный характер и должны
случайно сочетаться с различными
отклонениями![]() .
При наличии значительного перевеса
совпадений или несовпадений таких
отклонения делается предположение о
наличии связи междух
и y.
.
При наличии значительного перевеса
совпадений или несовпадений таких
отклонения делается предположение о
наличии связи междух
и y.
Один из простейших показателей тесноты связи разработан австрийским психиатром Г.Фехнером:
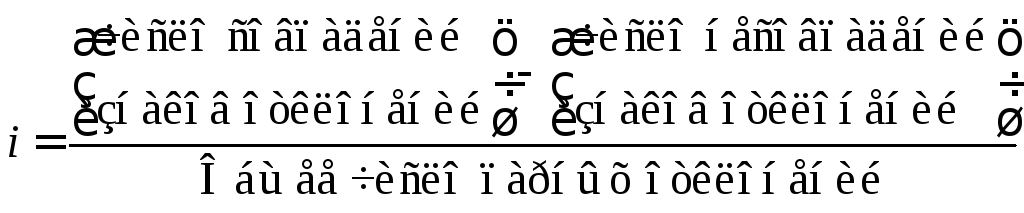 (1).
(1).
Показатель Фехнера изменяется от [-1;1], при значении равном 1 он указывает на полную прямую связь, при значении –1 на полную обратную связь, при i=0 связь отсутствует. Промежуточные значения i характеризуют степень близости связи к функциональной.
Например, для данных примера 1 рассчитаем средние значения для х и у:
![]()
![]()
Таблица 3. Расчет коэффициента Фехнера для оценки степени зависимости потребления электричества от объема выпуска продукции
|
Выпуск продукции |
5 |
7 |
10 |
12 |
15 |
17 |
|
Потребление эл-ва |
17 |
22 |
26 |
24 |
30 |
42 |
|
|
-6 |
-4 |
-1 |
1 |
4 |
6 |
|
|
-9,83 |
-4,83 |
-0,83 |
-2,83 |
3,17 |
15,17 |
![]()
![]()
Можно считать связь достаточно сильной.
Недостаток показателя Фехнера состоит в том, что разные по абсолютной величине отклонения имеют одинаковый вес.
Самый известный измеритель тесноты связи между признаками - линейный коэффициент корреляции Пирсона (назван по имени английского статистика К.Пирсона, введшего это коэффициент в научный анализ), он характеризует тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости.
Что представляет собой этот коэффициент?
Вновь используем для расчета данные примера 1. Запишем расчеты в виде среднего значения совместных отклонений признаков от их средних значений:
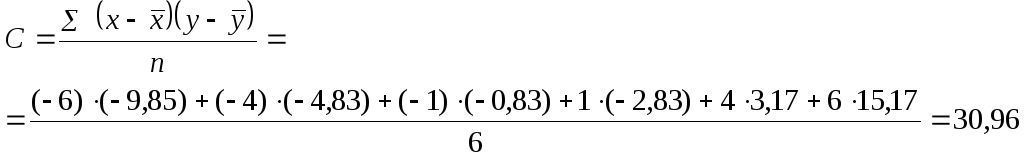 (2)
(2)
Полученное значение
называется коэффициентом
ковариации.
Это – мера совместной вариации признаков.
Или мы можем сказать, что это – мера
соответствия вариации результативного
признака вариации факторного. Недостатком
коэффициента ковариации является то,
что он не нормирован. Для преодоления
этого недостатка можно полученное
выражение разделить на среднее
квадратическое отклонение по х
и по y.
![]()
![]() (3).
(3).
Полученное значение
– линейный коэффициент корреляции,
показатель интенсивности линейной
связи. Это - безразмерная величина,
которая изменяется в интервале от –1
до +1,![]() .
Существует эмпирическое правило,
согласно которомукачественная оценка
связи между признаками производится
по шкале Чеддока:
.
Существует эмпирическое правило,
согласно которомукачественная оценка
связи между признаками производится
по шкале Чеддока:
|
|
Связь |
|
Связь |
|
0 0-0,2 0,2-0,3 0,3-0,5 |
Отсутствует Очень слабая Слабая Умеренная |
0,5-0,7 0,7-0,9 0,9-0,99 1 |
Заметная Тесная Весьма тесная Функциональная |
Путем ряда преобразований можно получить следующие аналитические выражения для коэффициента корреляции:
![]() (4).
(4).
![]() (5)
(5)
Производя расчет по итоговым значениям исходных переменных, линейный коэффициент корреляции можно вычислить по формуле:
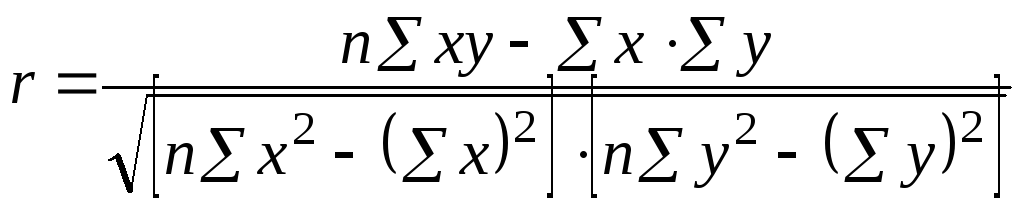 (6).
(6).
Линейный коэффициент корреляции имеет большое значение при исследовании социально-экономических явлений и процессов, распределения которых близки к нормальному.
