
моделирование / LabNo7
.pdf
Лабораторная работа №7 Построение моделей нелинейного программирования
7.1 Цель работы
Решение оптимизационных задач с использованием моделей нелиней-
ного программирования.
7.2 Задание на лабораторную работу
Построить модель нелинейного программирования, используя метод неопределенных множителей Лагранжа и найти решение задачи нелинейной оптимизации.
7.3 Порядок выполнения работы
Задачи нелинейной оптимизации с точки зрения методов решения делят-
ся на два класса:
 задачи безусловной оптимизации;
задачи безусловной оптимизации;
 задачи условной оптимизации.
задачи условной оптимизации.
Задача безусловной оптимизации представляет собой поиск оптимума целевой функции без всяких дополнительных условий, что записывается:
f ( x ) |
m ax(m in) |
Такие задачи на практике встречаются крайне редко, но метод их решения служит основой для решения практических задач оптимизации.
Задача условной оптимизации в общем случае записывается в виде:
F |
|
f ( x j ) |
|
max |
|||
g i ( x j ) |
bi |
|
|
|
|||
d j |
|
x j |
D j |
|
|
|
|
|
|
|
|
|
|
|
|
i |
1, m ; |
j |
1, n |
||||
Такая задача оптимизации кроме целевой функции включает дополни-
тельные условия в виде ограничений и граничных условий.

Наибольшее или наименьшее значение функции без учета того, где на-
ходится такое значение, – внутри заданного интервала или на его границе – называют оптимумом. Оптимум – более широкое понятие, чем экстремум.
Согласно определению признака экстремума, функция f ( x ) имеет мак-
симум (минимум) в точке x * , если в достаточной близости от этой точки всем значениям x соответствуют значения f ( x ) меньшие (большие), чем f ( x * ) .
Для случая максимума это показано на рис. 6.1.
Рис.6.1 |
Рис.6.2 |
Максимум и минимум функции объединяются понятием экстремум, ко-
торый может быть как локальным, так и глобальным. На рис. 6.2 функция f ( x ) принимает максимальные значения в вершинах В и D. При этом В > D.
В таком случае говорят, что точка В является глобальным максимумом, а
точка D – локальным. Аналогично функция f ( x ) принимает минимальные значения в точках А, С, Е, причем С < А < Е. В этом случае С будет глобаль-
ным минимумом, а А и Е – локальными минимумами. Из приведенных при-
меров видно, что глобальным максимумом (минимумом) называют такой максимум (минимум), который больше (меньше) всех остальных.
Достаточно часто при введении граничных условий типа x 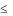 b , показан-
b , показан-
ных на рис. 6.3, наибольшее значение функции находится на границе в точ-
ке x 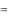 b . При этом величина f ( x ) не удовлетворит приведенному выше при-
b . При этом величина f ( x ) не удовлетворит приведенному выше при-
знаку экстремума.

Рис. 6.3
В таких случаях говорят, что в точке x  b находится оптимум функ-
b находится оптимум функ-
ции f (b )  B .
B .
Если экстремум есть не у всех функций, то в практических задачах оп-
тимум, как правило, есть всегда. Так же как и экстремумы, оптимумы могут
быть локальными и глобальными.
Существующие методы дают возможность находить только локальные оп-
тимумы. Если же есть подозрение, что в заданном интервале a j 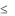 x j b j целе-
x j b j целе-
вая функция f ( x j ) может иметь несколько оптимумов, то этот интервал сле-
дует разбить на n интервалов, в каждом интервале определить свои локаль-
ные оптимумы, а затем из всех локальных оптимумов выбрать глобальный. В
таком случае задача нахождения глобального оптимума сводится к решению ряда задач, в которых ищется локальный оптимум.
В дальнейшем мы будем рассматривать нахождение только локального оп-
тимума. Следует отметить, что в подавляющем большинстве практических экономических и технических задач оптимизации существует только один оптимум.
Решение задачи безусловной оптимизации
Задачи нелинейной оптимизации могут решаться различными методами.
Методы, реализованные в Excel, относятся к методам поиска. Метод поиска экстремума функции произвольного числа переменных производится сле-
дующим образом. |
|
|
||
|
Прежде всего надо задаться координатами начальной точки поиска x j |
0 , |
||
|
|
|
0 была как можно |
|
j 1, n . Желательно, чтобы выбранная начальная точка x j |
||||
ближе к искомому экстремуму, что сократит время поиска. Но как же такую точку выбрать? Если решается реальная задача, то специалист всегда знает ожидаемую область нахождения экстремума, в которой и следует задать на-
чальную точку. Если решающий задачу не является специалистом в данной области, то обязательные требования заключаются в том, чтобы целевая функция в начальной точке не была равна нулю.
|
|
|
f ( x |
0 ) 0 . |
|
|
|
|
j |
Это необходимо, чтобы не было деления на ноль при вычислении Fk . |
||||
|
|
|
|
|
Итак, x j |
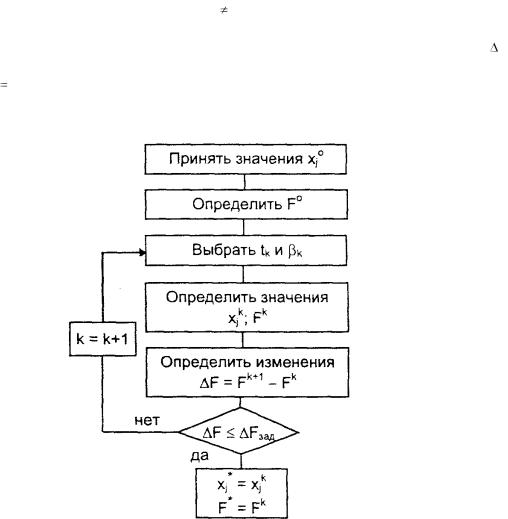
0 , j 1, n выбрана. Блок-схема алгоритма поиска приведена на рис. |
|||
6.4. |
|
|
|
|
Рис. 6.4
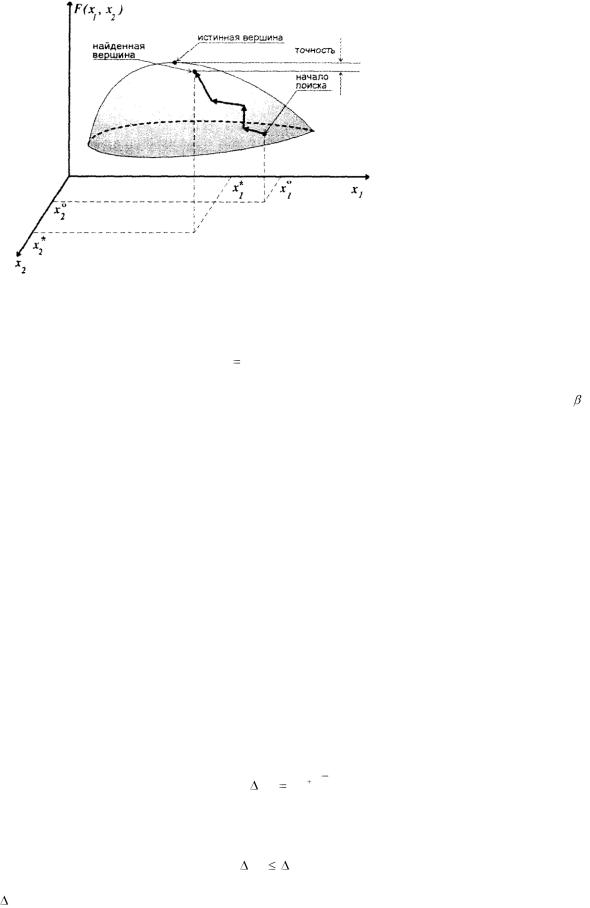
Графическое изображение такого движения для случая поиска мак-
симума при j = 1,2 показано на рис. 6.5.
|
|
|
|
Рис.6.5 |
|
Идея поиска экстремума заключается в следующем: |
|||||
|
|
|
|
|
|
1. |
Задать начальную точку x |
0 , j 1, n . |
|||
|
|
|
j |
||
2. |
В заданной точке x j |
0 определить направление движения на первом шаге 1 |
|||
3.Принять величину шага ti .
4.Определить координаты конца первого шага x j 0 .
5.Вычислить значения признака экстремума на первом шаге.
6.Проверить выполнение признака экстремума.
Если условие признака выполняется, то принимается, что экстремум находится в точке x j 0 , если нет – аналогично выполняется второй шаг и так далее до выполнения условия, характеризующего достижение экстремума.
Важный вопрос поиска – признак достижения экстремума, т. е. верши-
ны. В Excel таким признаком является величина относительного приращения функции на каждой итерации:
Fk |
Fk 1 Fk |
. |
|
||
|
Fk |
|
Экстремум считается достигнутым, если выполняется условие
Fk Fзад ,
где Fзад – точность, назначаемая при решении задачи.

В приведенном алгоритме мы ничего не сказали о том, как же выбирать направление и длину шага на каждой итерации. А этот вопрос является ис-
ключительно важным, т. к. именно он определяет точность полученных ре-
зультатов и быстроту сходимости, т.е. число итераций, за которое будет дос-
тигнут экстремум. Методы выбора направления и длины шага бывают раз-
личных типов. Рассмотрим некоторые из них, реализованные в Excel.
Методами поиска называются такие методы, которые для определения направления 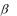 и величины шага t используют только значение целевой функции. Такие методы называют также методами нулевого порядка.
и величины шага t используют только значение целевой функции. Такие методы называют также методами нулевого порядка.
Градиентные методы или методы первого порядка – это такие методы,
в которых для определения направления  и шага t используются значения первых производных целевой функции и определяется ее градиент.
и шага t используются значения первых производных целевой функции и определяется ее градиент.
Методами Ньютона или методами второго порядка называются такие методы, в которых для определения направления 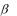 и шага t используются значения вторых производных целевой функции.
и шага t используются значения вторых производных целевой функции.
Чем выше порядок методов, тем больше вычислений на каждой итера-
ции, но тем меньше требуется итераций. И, естественно, наоборот. Наиболее распространенными являются градиентные методы. Такое положение объяс-
няется тем, что с одной стороны, они не требуют на каждой итерации очень больших вычислений, т.к. вычисляется только целевая функция и ее первые производные, а с другой – у этих методов достаточно хорошая сходимость,
т.е. они обеспечивают нахождение экстремума за небольшое число итераций.
Градиентные методы по способу определения направления  и шага t име-
и шага t име-
ют много разновидностей.
Таковы основные идеи поиска решения в задачах безусловной оптимизации.
Пример. Определить градиентным методом max функции:
f ( x1 , x 2 ) 4 x1 2 x 2 x12 x 22 5
Решить задачу методом градиентного спуска.
Решение. За начальную точку выберем x 0 (4,5) ; f(x)=-20.
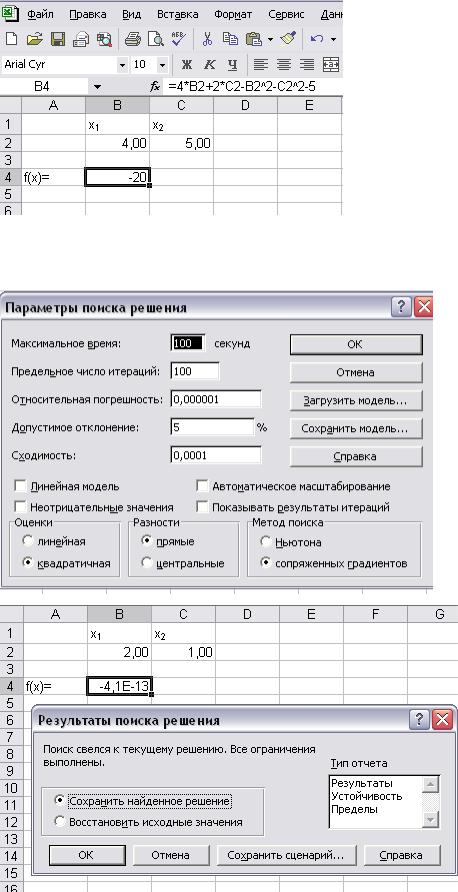
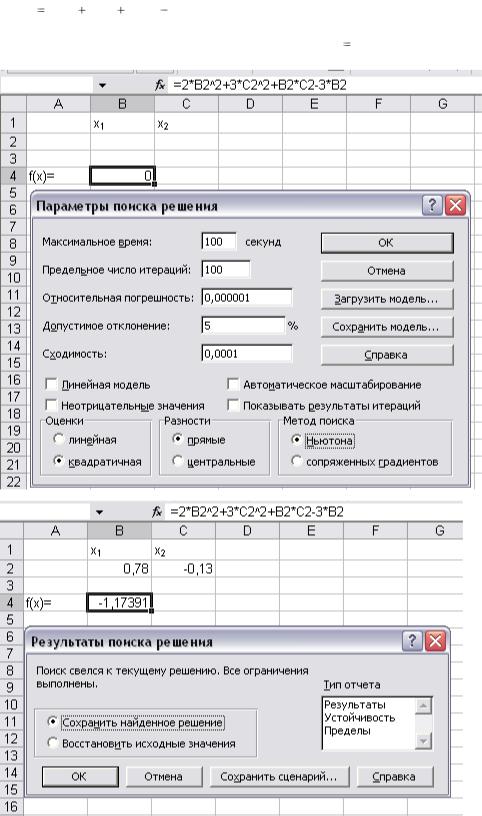
C помощью соответствующих настроек меню ПАРАМЕТРЫ, процедуры ПОИСК РЕШЕНИЯ получим следующий результат.
Таким образом, точка (2,1) является стационарной и значение функции f(2,1)=0.
Правильность полученного результата предлагаем проверить Вам с помощью алгоритма метода градиентного спуска [ ].
Пример. Определить методом Ньютона минимум функции:
f ( x ) 2 x12 3 x 22 x1 x 2 3 x1
Решение. За начальную точку выберем x 0 (0,0).
Таким образом, точка (0,78;-0,13) является стационарной и значение мини-

мума функции f(x)= -1.17391.
Правильность полученного результата предлагаем проверить Вам с помощью алгоритма метода Ньютона [ ].
Решение задачи условной оптимизации
Общий случай задачи оптимизации
F |
|
f ( x j ) |
|
max |
|||
g i ( x j ) |
bi |
|
|
|
|||
d j |
|
x j |
D j |
|
|
|
|
|
|
|
|
|
|
|
|
i |
1, m ; |
j |
1, n |
||||
является задачей условной оптимизации. Есть целый ряд методов решения таких задач. Рассмотрим реализованный в Excel метод множителей Лагран-
жа, идея которого заключается в преобразовании задачи условной оптимиза-
ции в задачу безусловной оптимизации, что производится следующим обра-
зом.
1. Преобразовать ограничения-неравенства в уравнения
bi g i ( xi ) |
0 |
|
|||||
|
|
|
|
|
|
|
|
i |
1, m ; |
j |
1, n . |
||||
2. Составить функцию Лагранжа |
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
L ( x j , j ) f ( x j |
) |
|
j |
(bi g i ( x i )) max |
|||
|
|
|
i |
1 |
|
|
|
j – множитель Лагранжа.
Физический смысл множителей Лагранжа поясним чуть позже при рас-
смотрении примера.
3. Определить частные производные и составить систему уравнений
L ( x j , |
i ) / |
x j |
0 |
L ( x j , |
i ) / |
x j |
0 |
i 1, m ; j 1, n
4. Решая систему, определить значения j .
5. Подставить значения j в функцию Лагранжа. Получим задачу безуслов-
ной оптимизации.
6. Полученную задачу безусловной оптимизации решить методами, рассмот-
ренными выше.
Проиллюстрируем метод множителей Лагранжа следующим примером:
F ( x1 , x2 ) |
|
x1 |
x2 |
min |
(1) |
|||
x 2 |
|
|
2 |
|
|
|
|
|
x |
1 |
|
|
|
||||
1 |
|
|
2 |
|
|
|
|
|
1. Запишем систему (1) в следующем виде: |
|
|
|
|||||
F ( x1 j ) |
x1 |
x 2 |
min |
(2) |
||||
|
|
2 |
|
|
2 |
|
|
|
1 |
x1 |
|
x 2 |
0 |
|
|
||
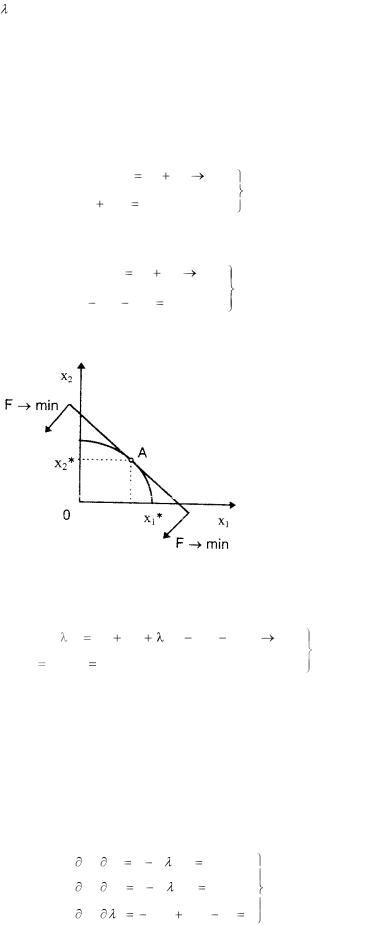
Графическое решение задачи (2) представлено на рис. 6.6..
Рис.6.6
2. Составим функцию Лагранжа
L( x , ) |
x |
|
x |
|
|
(1 x 2 |
x 2 ) |
m in |
(3) |
j i |
|
1 |
|
2 |
1 |
1 |
2 |
|
|
|
|
|
|
||||||
j 1, 2; i |
1 |
|
|
|
|
|
|
|
|
В (3) видно, что множитель Лагранжа определяет, как изменится целевая функция при изменении правой части в данном ограничении на единицу.
Следовательно, множитель Лагранжа в нелинейной задаче - это аналог двой-
ственной оценки в линейной задаче. 3. Запишем систему уравнений
L / |
x1 |
1 |
2 |
1 x1 |
0 |
|
L / |
x 2 |
1 |
2 |
1 x 2 |
0 |
(4) |
L / |
1 |
|
( x1 2 |
x 2 2 |
1) |
0 |
4. В результате решения системы (4) найдем
