
моделирование / LabNo3
.pdf
Лабораторная работа №3
Построение и решение двойственных целочисленных моделей.
3.1. Цель работы
Построение моделей целочисленного линейного программирования и их решение методом ветвей и границ.
3.2. Задание на лабораторную работу
Найти оптимальное решение задачи целочисленного линейного программирования методом ветвей и границ, используя средства Excel.
3.3. Порядок выполнения работы
I. Метод ветвей и границ представляет собой метод отсекающей
плоскости. Алгоритм метода ветвей и границ заключается в следующем.
1. Решается исходная задача |
ЗЛП-1, |
определяется |
оптимальное |
решение |
||||
|
|
|
|
|
|
|
||
х* = (х1* , х*2 ,..., х*n ), f(х* ) = f. |
Если х*j |
0, целые, |
j = 1, m , то |
решение |
||||
закончить, если нет, переходят к шагу 2. |
|
|
|
|
||||
2.Выбирается по установленному правилу координата xk = x*k. Это может быть, например, координата с наибольшей или наименьшей дробной частью, наибольшим или наименьшим порядковым номером и пр.
Выделяется целая часть [x*k] и строятся два ограничения: xk [x*k]; xk 
[x*k] + 1.
3. Решается задача ЗЛП-2, которая представляет собой ЗЛП-1 с ограничением
xk [x*k].
4. Решается задача ЗЛП-3, которая представляет собой ЗЛП-1 с ограничением
xk [x*k] +1.
5.Если ни одна из задач ЗЛП-2, ЗЛП-3 не дала целочисленного решения, то каждая из них ветвится на две в соответствии с шагом 2. Ветвление продолжается до тех пор пока в одной из ветвей не будет найдено целочисленное решение x . Значение функции ( f(x) ) на этом решении есть f

- нижняя граница возможных максимальных решений f(x) на целочисленном решении.
6. Если значение целевой функции fi на оптимальных нецелых решениях во
всех ветвях не превышает f, то ветвление закончено и |
~ |
есть искомое |
x |
решение задачи. Если в какой-то ветке fi > f, то ее решение следует продолжать.
7. Критерий окончания fi ≤ f, i.
ПРИМЕР. С помощью симплекс-процедуры, реализованной в EXCEL,
решить следующую задачу методом ветвей и границ. Построить схему решения данной задачи.
F = 7 x1 + 3 x2 m a x
5 x1 |
+ 2 x2 |
2 0 |
8 x1 |
+ 4 x2 |
3 8 |
x1 , x2 0 ,ц елы е
Решение.
1. С помощью диалогового окна ПОИСК РЕШЕНИЯ определяем решение задачи ЗЛП-1:
Замечание.
В окне ввода ограничений не нужно указывать на условие целочисленности переменных. Цель задания – усвоить алгоритм метода ветвей и границ.
F = 7 x1 + 3 x2 m a x
5 x1 |
+ 2 x2 |
2 0 |
8 x1 |
+ 4 x2 |
3 8 |
x1 , x2 0 |
|
|

Вывод: ЗЛП-1 не дает целочисленного решения.
2. Выбираем координату x2=7,5; выделяем целую часть [x2] = 7; строим два ограничения: x2 ≤ 7; x2 ≥ 8. Составим задачи ЗЛП-2 и ЗЛП-3 с новыми граничными условиями.
ЗЛП-2: |
|
ЗЛП-3: |
|
||||
F = 7 x1 + 3 x2 m a x |
F = 7 x1 + 3 x2 m a x |
||||||
5 x1 + 2 x2 |
2 0 |
5 x |
1 |
+ 2 x |
2 |
2 0 |
|
|
|
|
|
|
|
||
8 x1 + 4 x2 |
3 8 |
8 x |
1 |
+ 4 x |
2 |
3 8 |
|
|
|
|
|
|
|
||
x2 7 |
|
|
x2 |
|
8 |
|
|
|
|
|
|
|
|
||
x1 , x2 |
0 |
|
x1 , x2 0 |
|
|||
|
|
|
|
||||
3. |
Определяем решение задачи ЗЛП-2. |
|
|
|
|||

Вывод: ЗЛП-2 не дает целочисленного решения.
4. Определяем решение задачи ЗЛП-3.
Вывод: ЗЛП-3 не дает целочисленного решения.
5. Так как ни одна из задач ЗЛП-2 и ЗЛП-3 не дала целочисленного решения,
то каждая из них ветвится на две в соответствии с шагом 2 алгоритма.
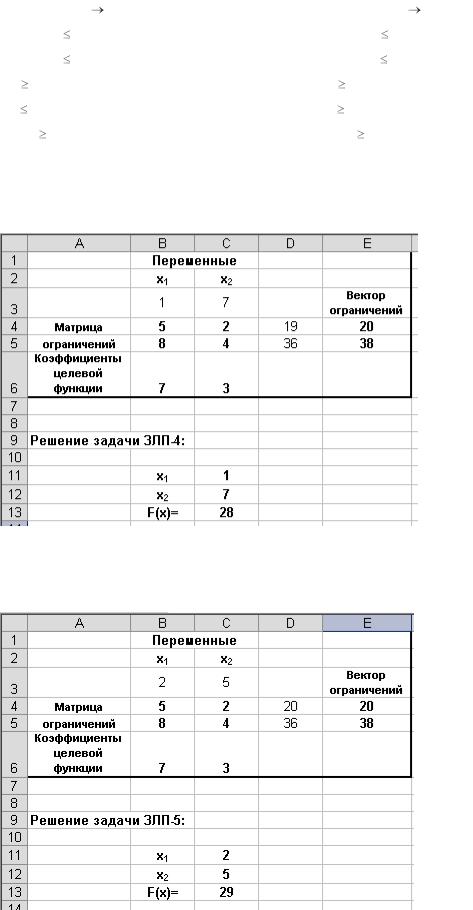
Составим задачи ЗЛП-4 (ЗЛП-2 + дополнительное ограничение x1 ≤ 1) и ЗЛП- 5(ЗЛП-2 + дополнительное ограничение x1≥2), ЗЛП-6 (ЗЛП-3 +
дополнительное ограничение x1 ≤ 0) и ЗЛП-7 (ЗЛП-3 + дополнительное
ограничение x1 ≥1) |
|
|
|
||
ЗЛП-4: |
|
|
ЗЛП-5: |
||
F = 7 x1 + 3 x2 m a x |
F = 7 x1 + 3 x2 m a x |
||||
5 x1 + 2 x2 |
2 0 |
5 x1 + 2 x2 |
2 0 |
||
8 x1 + 4 x2 |
3 8 |
8 x1 + 4 x2 |
3 8 |
||
x2 |
7 |
|
x2 |
7 |
|
x1 |
1 |
|
x1 |
2 |
|
x1 , x2 0 |
|
x1 , x2 0 |
|
||
ЗЛП-6: |
ЗЛП-7: |
F = 7 x1 + 3 x2 m a x |
F = 7 x1 + 3 x2 m a x |
||||||
5 x1 + 2 x2 |
2 0 |
5 x1 + 2 x2 |
2 0 |
||||
8 x1 + 4 x2 |
3 8 |
8 x1 + 4 x2 |
3 8 |
||||
x2 |
|
8 |
|
x2 |
|
8 |
|
x1 |
0 |
|
x1 |
1 |
|
||
x1 , x2 |
0 |
|
x1 , x2 |
0 |
|
||
6. Определяем решение ЗЛП-4.
Вывод: получено целочисленное решение.
7. Определяем решение ЗЛП-5.
Вывод: получено целочисленное решение. Значение функции на этом решении f5(x) есть нижняя граница f возможных максимальных решений на целочисленном решении.
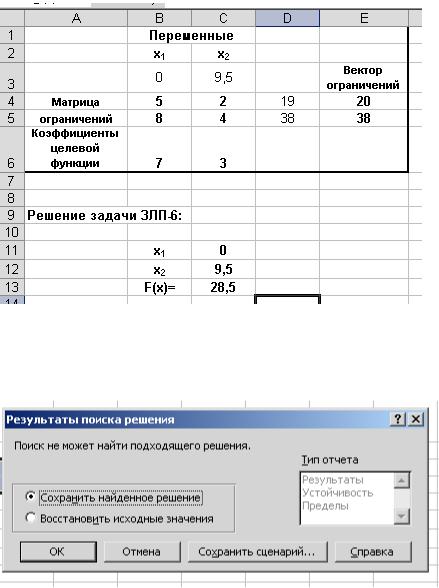
8. Определяем решение ЗЛП-6.
Вывод: решение не является целочисленным и значение целевой функции на этом решении не превышает f = f5(x) = 29. Ветвление закончено.
9. Определяем решение ЗЛП-7. Эта задача решения не имеет.
10. В соответствии с алгоритмом оптимальное решение получено в ветви,
соответствующей ЗЛП-5: x1=2, x2=5, f(x)=29.

Схема решения задачи методом ветвей и границ
ЗЛП - 1
x1 = 1 x2 = 7,5 f(x) = 29,5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗЛП – 2 |
|
|
|
|
|
|
|
|
|
ЗЛП – 3 |
|
|
||||||
|
|
(ЗЛП-1 + x2 ≤ 7) |
|
|
|
|
|
|
|
|
|
(ЗЛП-1 + x2 ≥ 8 ) |
|
|
||||||
|
|
x1 = 1,2 |
x2 = 7 |
|
|
|
|
|
|
|
|
|
x1 = 0.75 |
x2 = 8 |
|
|
||||
|
|
f(x) = 29,4 |
|
|
|
|
|
|
|
|
|
f(x) = 29,25 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗЛП – 4 |
|
|
ЗЛП – 5 |
|
|
|
|
ЗЛП – 6 |
|
|
ЗЛП – 7 |
|||||||||
(ЗЛП-2 + x1 ≤ 1) |
|
|
(ЗЛП-2 + x1 ≥ 2 ) |
|
|
|
|
(ЗЛП-3 + x1 ≤ 0) |
|
|
(ЗЛП-3 + x1 ≥ 1 ) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
не имеет |
||
x1 = 1 x2 = 7 |
|
|
x1 = 2 x2 = 5 |
|
|
|
x1 = 0 x2 = 9,5 |
|
|
решения |
||||||||||
f(x) = 28 |
|
|
f(x) = 29 |
|
|
|
|
f(x) = 28,5 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Варианты заданий
Построить двойственную модель целочисленного программирования и
получить решение методом ветвей и границ.
1 . f(x) = 2x1 + x2 |
m ax |
2 . f ( x ) 70 x 1 30 x 2 |
max |
|||||||
7x1 |
3 x2 |
21 |
|
10 x 1 |
4 x 2 |
40 |
|
|
||
x1 + x2 |
5 |
|
6 x 1 |
4 x 2 |
36 |
|
|
|||
0 |
x1 |
3 |
|
|
x 1 , x 2 |
0 |
|
|
|
|
0 |
x2 |
5 |
|
|
|
|
|
|
|
|
x1 , x2 |
0 |
|
|
|
|
|
|
|
|
|
3 . f(x) = 3x1 + 3x2 |
m ax |
4 . f(x) = 3x1 + 2x2 |
m ax |
|
||||||
4x1 |
5x2 |
20 |
|
3x1 |
7x2 |
21 |
|
|
||
x1 + 6x2 |
|
12 |
|
x1 + x2 |
4 |
|
|
|
||
0 |
x1 |
5 |
|
|
0 |
x1 |
4 |
|
|
|
0 |
x2 |
4 |
|
|
0 |
x2 |
3 |
|
|
|
x1 , x2 |
0 |
|
|
x1 , x2 |
0 |
|
|
|
||

5 . |
f(x) = 1x1 + 3x2 |
m ax |
6 . |
f(x) = 4x1 + 1x2 |
m ax |
|||||||
3x1 |
4x2 |
|
12 |
|
|
|
2x1 |
3x2 |
6 |
|
||
3x1 + 2x2 |
|
6 |
|
|
|
4x1 + 9x2 |
18 |
|
||||
0 |
x1 |
4 |
|
|
|
|
0 |
x1 |
2 |
|
|
|
0 |
x2 |
|
2 |
|
|
|
|
0 |
x2 |
3 |
|
|
x1 , x2 |
0 |
|
|
|
|
x1 , x2 |
0 |
|
|
|||
7 . |
f(x) = 3x1 + x2 |
m ax |
8 . |
f(x) = x1 |
+ 2x2 |
m ax |
||||||
4x1 |
3x2 |
|
18 |
|
|
|
5x1 |
9 x2 |
4 5 |
|
||
x1 + 2x2 |
|
|
6 |
|
|
|
x1 + 3x2 |
12 |
|
|||
0 |
x1 |
5 |
|
|
|
|
0 |
x1 |
9 |
|
|
|
0 |
x2 |
|
3 |
|
|
|
|
0 |
x2 |
4 |
|
|
x1 , x2 |
0 |
|
|
|
|
x1 , x2 |
0 |
|
|
|||
9 . |
f(x) = x1 + 2x2 |
+ x5 |
m in |
1 0 . |
f(x) = 3x1 - 2x 2 |
m ax |
||||||
x1 |
x2 |
|
x3 |
x4 |
x5 |
5 |
2x1 |
3 x2 |
6 |
|
||
x2 |
x3 |
|
|
x4 |
x5 |
2 |
|
x1 - 2x2 |
2 |
|
|
|
x3 |
x4 |
|
|
x5 |
1 |
|
|
0 x1 |
3 |
|
|
|
xi |
0 |
|
|
|
|
|
|
0 |
x2 |
3 |
|
|
|
|
|
|
|
|
|
|
x1 , x2 |
0 |
|
|
|
1 1 . |
f(x) = |
x1 |
m ax |
|
1 2 . |
f(x) = x1 + 2x2 |
m ax |
|||||
x1 |
x2 |
|
x3 |
9 |
|
|
5x1 |
9 x2 |
45 |
|
||
-4x1 + 7x2 |
x4 |
4 |
|
x1 + 3x2 |
12 |
|
||||||
5x1 - 6x2 |
|
x5 |
6 |
|
|
0 x1 |
9 |
|
|
|||
xi |
0 |
|
|
|
|
|
|
0 |
x2 |
4 |
|
|
|
|
|
|
|
|
|
|
x1 , x2 |
0 |
|
|
|
1 3 . |
f(x) = 2 x1 + x2 |
|
m ax |
1 4 . f(x) = 2x1 + x 2 |
m ax |
|||||||
6 x1 |
4 x2 |
|
x3 = 2 4 |
|
7x1 + 3x2 |
21 |
|
|||||
3 x1 - 3 x2 |
|
x4 = 9 |
|
|
x1 + x2 |
5 |
|
|
||||
-x1 |
3 x2 |
|
x5 |
3 |
|
|
0 |
x1 |
3 |
|
|
|
x1 , x2 , x3 , x4 , x5 |
0 |
|
|
0 |
x2 |
5 |
|
|
||||
1 5 . f(x) = x1 + x2 |
m ax |
1 6 . f(x) = x1 + 4x 2 |
m ax |
|||||||||
2x1 + x2 + x3 = 6 |
|
|
-x1 + 2x2 + x3 = 2 |
|
||||||||
2x1 + 3x2 + x4 |
9 |
|
|
3x1 + 2x2 + x4 = 6 |
|
|||||||
x j |
0 |
|
|
|
|
|
|
x j |
0 |
|
|
|
Контрольные вопросы
1.По какому правилу строятся отсекающие плоскости в методе ветвей и границ? Какие методы решения задач целочисленного линейного программирования Вы знаете?
2.Какими свойствами обладает отсекающая плоскость?
