
моделирование / LabNo4
.pdf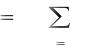
Лабораторная работа №4
Построение моделей и решение задач стохастического программирования
4.1. Цель работы
Решение задачи стохастического программирования (линейная модель).
4.2. Задание на лабораторную работу
Определить количественные характеристики случайной величины, построить графики плотности и функции распределения (для случая нормального закона распределения), поставить задачу стохастического программирования и решить ее.
4.3. Порядок выполнения работы
Универсальных методов решения задач стохастического программирования, пригодных для всех классов задач оптимизации, нет. Будем рассматривать решение только одного распространенного на практике класса стохастических задач - стохастических задач линейного программирования применительно к распределению ресурсов.
Прежде чем приступить к решению таких задач, вспомним некоторые понятия из теории вероятностей. Случайной величиной называется такая величина, которая может принять то или иное значение, причем заранее неизвестно, какое именно. Примерами таких величин могут служить параметры моделей. В задачах распределения ресурсов случайной величиной может быть фактическое количество располагаемого ресурса. Математическое ожидание случайной величины, которое будем обозначать M[x], определяет ее среднее значение
|
1 |
|
n |
|
M [ x ] |
|
x i , |
||
|
|
|||
n i |
||||
|
1 |
|||
где xi - значение случайной величины в i -ой реализации, n - число реализаций.
В Excel математическое ожидание определяется с помощью функции СРЗНАЧ (значения чисел) в категории Статистические.
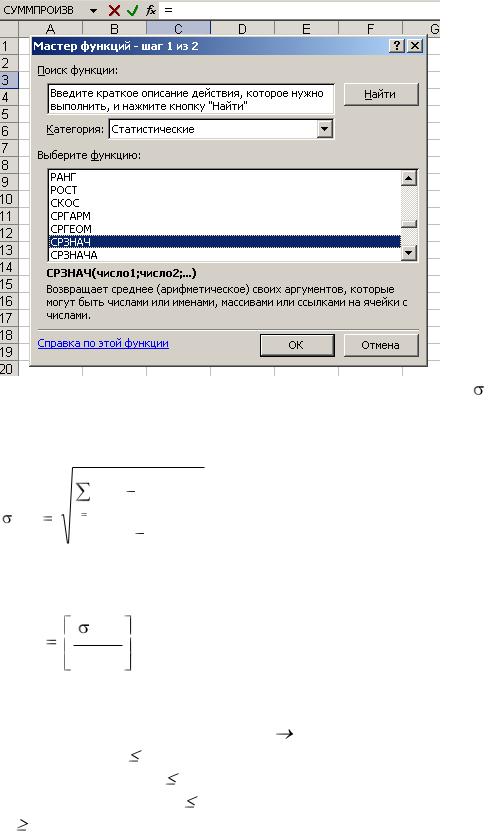
Среднее квадратическое отклонение, обозначаемое [x], определяет разброс значений случайной величины относительно ее математического ожидания. Заметим, что в Excel эта величина называется стандартное отклонение - СТАНДОТКЛОН (значения чисел) по зависимости
|
n |
|
|
|
( x i |
M [ x ]) 2 |
|
[ х ] |
i 1 |
|
|
n |
1 |
||
|
Третьей важной количественной характеристикой случайной величины, которая показывает относительную величину разброса случайных величин, является коэффициент вариабильности
[ x ]
v[ x ]
M [ x ]
Определение этих характеристик случайной величины проиллюстрируем на следующем примере. Решая задачу распределения ресурсов
f (x) = 60x1 + 70x2 + 120x3 + 130x4 max
x1 + x2 + x3 + x4 16 |
|
|||
6x1 |
+ 5x2 |
+ |
4x3 + 3x4 |
110 |
4x1 |
+ 6x2 |
+ |
10x3 + 13x4 |
100 |
xj |
0 , j = 1,2,3,4 |
|
||
мы принимали, что числовые значения cj, aij, bi известны и равны тем величинам, которые указаны в этой системе. Если же эти величины являются случайными, то для дальнейшей работы необходимо определить их количественные характеристики. Определение таких характеристик рассмотрим на примере исходных данных для располагаемого сырья.

Алгоритм. Определение количественных характеристик случайной величины
1.Ввести в таблицу замеренные значения случайной величины и определить характеристики (математическое ожидание, стандартное отклонение, коэффициент вариабильности)(рис.3.1).
Рис.4.1
2. Нормальный закон распределения случайной величины
Наиболее полной характеристикой случайной величины является закон ее распределения. Законов распределения предложено достаточно много. На практике наибольшее распространение получил нормальный закон распределения. Как и все законы распределения, нормальный закон имеет две формы представления:
плотность распределения f(x); функцию распределения F(x).
Эти формы вычисляются по следующим зависимостям:
плотность распределения
1 |
|
|
( x m )2 |
||||
|
|
2 |
2 |
|
|||
f ( x ) |
|
|
|
e |
, |
||
|
|
|
|
||||
|
|
||||||
2 |
|
|
|
||||
|
|
|
|
|
|||
где m = M[x] - математическое ожидание случайной величины; = [x] - среднеквадратическое отклонение;
функция распределения
|
x |
F ( x ) |
f ( x )dx , |
которая иногда называется интегральной функцией, имеет большое практическое значение, т.к. с помощью зависимости P(x a) = F(x) есть возможность определить вероятность появления случайной величины x a. График плотности распределения показывает, какие значения случайной величины наиболее вероятны. Теоретически случайная величина x может изменяться в пределах-
< x < .
Однако с точностью до долей процента случайная величина может находиться в интервале
M[x] - 3 [x] x M[x] + 3 [x],
что и принимается за пределы изменения случайной величины.
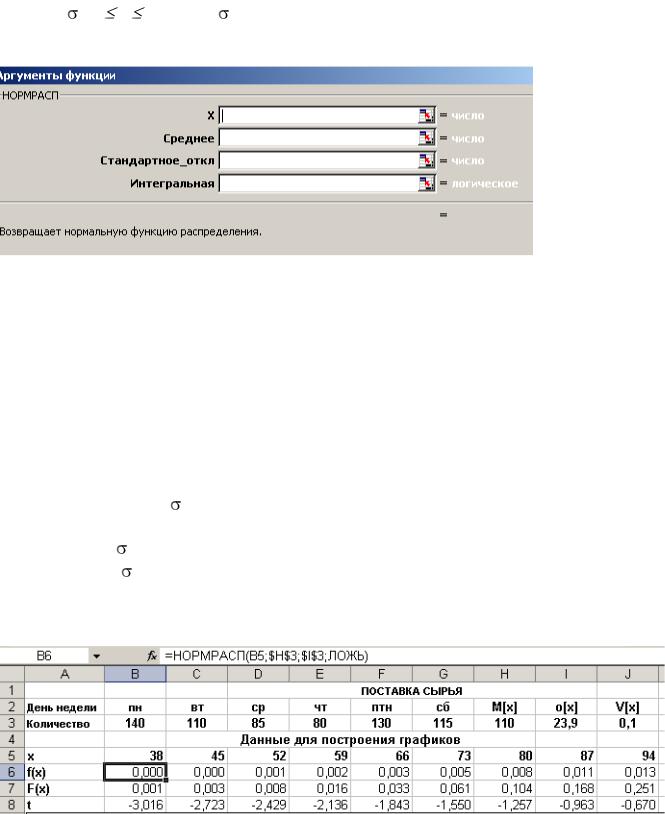
В EXCEL обе эти формы находятся с помощью функции НОРМРАСП:
где х - задаваемое значение случайной величины, для которой находятся значения f(х) или F(х);
среднее; стандартное_отклн - величины, определенные по алгоритму, изложенному выше; интегральная - определяет форму, для которой определяется значение.
При интегральная - ИСТИНА определяется значение интегральной функции, т.е. функции распределения F(х). При интегральная - ЛОЖЬ определяется значение плотности распределения f(х).
Алгоритм. Определение плотности и функции распределения для нормального закона
1.Определить M[x] , [x].
2.Найти пределы изменения случайной величины x:
xmin = M[x] - 3 |
[x] = 38, |
xmax = M[x] + 3 |
[x] = 181 |
3. Для получения плавных кривых f(x) и F(x) в интервале изменения случайной величины между xmin и xmax целесообразно принять примерно 20 промежуточных значений (рис.4.2).
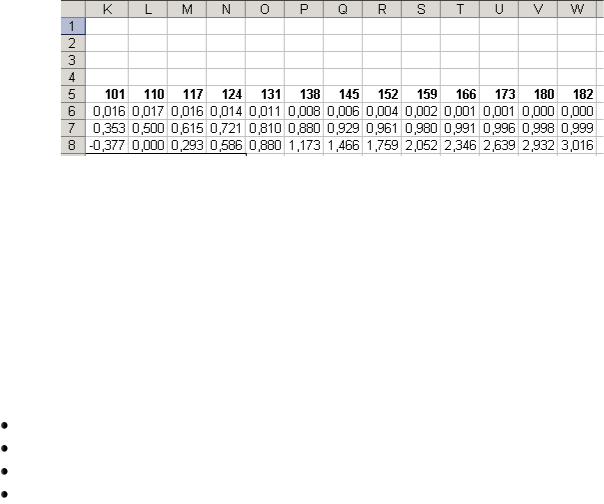
Рис. 4.2
4.Принятые значения, для которых будут вычисляться значения f(x) и F(x), ввести в ячейки B5:W5.
5.Для ячеек, в которых будут вычисляться значения f(x) и F(x) , назначить представление результата с тремя знаками после запятой.
6.Курсор в В6.
7.Мастер функций, Статистические, НОРМРАСП.
На экране: диалоговое окно НОРМРАСП.
8.Ввести (выделяя соответствующую ячейку): x – B5;
среднее – H3;
стандартное отклонение – I3; интегральный - ЛОЖЬ.
9. Готово.
На экране: В6 = 0,000.
10.Скопировать В6 в В7.
11.Курсор в В7.
12.В строке ввода в диалоговом окне изменить ЛОЖЬ на ИСТИНА.
13.<Enter>.
14.Выделить В6:В7 и скопировать протаскиванием до W6:W7.
На экране : искомые значения f(x) и F(x).
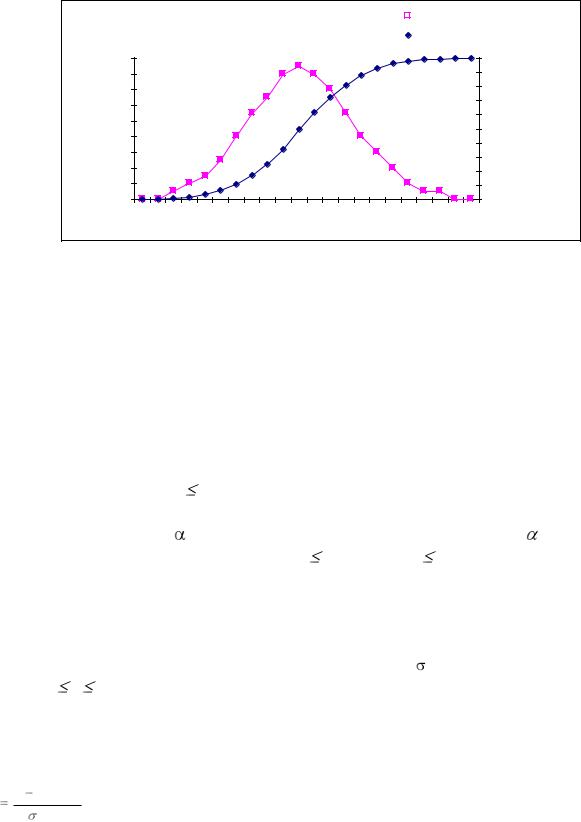
15. Построить графики плотности и функции распределения для нормального закона (рис.4.3).
0,018
0,016
0,014
0,012
f(x) 0,010 0,008
0,006
0,004
0,002
0,000
Гр а ф и к f(x ) и F (x ) |
|
|
|
|
f ( x ) |
|
|
|
|
||
|
|
|
|||
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
F( x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
,0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
,9 |
|
|
|
|
|
|
|
|
|
|
|
0 |
,8 |
|
|
|
|
|
|
|
|
|
|
|
0 |
,7 |
|
|
|
|
|
|
|
|
|
|
|
0 |
,6 |
|
|
|
|
|
|
|
|
|
|
|
0 |
,5 |
F(x) |
|
|
|
|
|
|
|
|
|
|
0 |
,4 |
|
|
|
|
|
|
|
|
|
|
|
0 |
,3 |
|
|
|
|
|
|
|
|
|
|
|
0 |
,2 |
|
|
|
|
|
|
|
|
|
|
|
0 |
,1 |
|
|
|
|
|
|
|
|
|
|
|
0 |
,0 |
|
38 |
52 |
66 |
80 |
94 |
10 |
24 |
38 |
52 |
66 |
80 |
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
1 |
1 |
|
|
Рис. 4.3
График плотности распределения f(x) показывает вероятность появления каждого вида случайной величины. Из построенного графика видно, что наиболее вероятно появление случайной величины для M[x] = 110, что совершенно закономерно, т.к. наиболее вероятным значением случайной величины является ее математическое ожидание.
Для определения вероятности появления случайной величины в некотором интервале используется график функции распределения. С его помощью можно решать две задачи: прямую и обратную Решение прямой задачи дает ответ на вопрос: какова вероятность того, что случайная величина x будет не менее а. Из графика видно, что Р(x 110) = 0,5. Обратная задача ставится так: чему должна быть равна случайная величина x, чтобы вероятность ее появления равнялась бы
заданному значению . Из графика |
видно, что вероятность |
= 0,8 будет |
справедлива для случайной величины x |
130, т.е. Р(x 130) = 0,8. |
|
Ответ на вопрос обратной задачи можно получить также с помощью функции НОРМОБР(вероятность, среднее; станд._откл).
При решении практических задач достаточно часто применяют закон
нормального |
стандартного распределения. Этот закон описывает вероятность |
появления случайной величины t, имеющей M[t] = 0, [t] = 1, в интервале |
|
-3 t |
3. |
Переход от случайной величины x к случайной величине t производится по зависимости
x M [ x ]
t
[ x ]
В Excel для этой цели применяется функция НОРМАЛИЗАЦИЯ(x; среднее; стандартное_откл.).

16. Построить график функции распределения для нормального стандартного распределения.
3. Варианты постановки задачи стохастического программирования
Если коэффициенты cj в целевой функции - случайные величины, то возможно две постановки задачи оптимизации:
 максимизация (минимизация) среднего значения целевой функции, которая называется М - постановкой:
максимизация (минимизация) среднего значения целевой функции, которая называется М - постановкой:
М[F] max (min);
 максимизация вероятности получения максимального (минимального) значения, которая называется Р - постановкой:
максимизация вероятности получения максимального (минимального) значения, которая называется Р - постановкой:
P[Fmax(min)] max ;
Если случайными являются величины aij и bi, входящие в ограничения, то i-ое ограничение
n |
|
|
|
|
aij x j |
bi |
|
|
|
j 1 |
|
|
|
|
записывается так: |
|
|
||
n |
|
|
|
|
P |
aij x j |
bi |
i , |
(1) |
j |
1 |
|
|
|
где |
i - заданная вероятность, с которой должно быть выполнено i-ое ограничение. |
|||
Запись граничных условий может быть выполнена в двух вариантах. Если в ограничении
dj |
xj |
Dj (2) |
dj |
, Dj |
- детерминированные величины, то ограничение остается в виде (2). Если dj , |
Dj - случайные величины, то (2) рассматривается как два ограничения
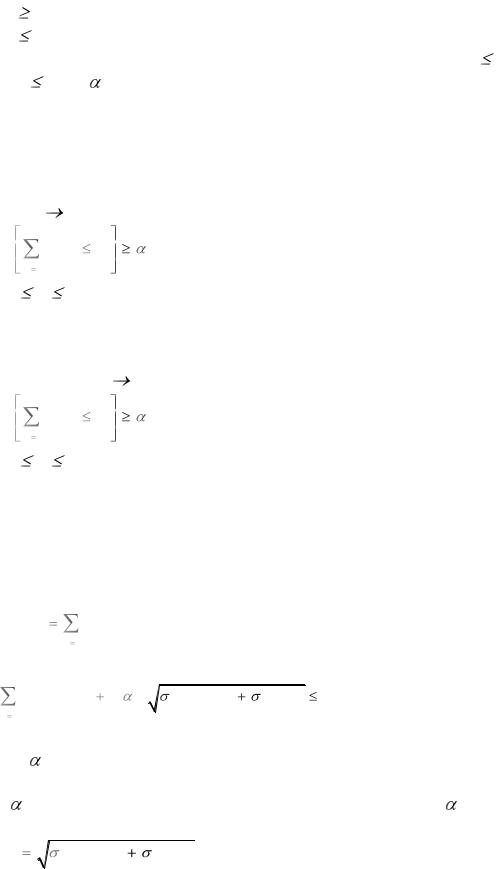
xj |
dj |
(3) |
xj |
Dj, |
|
при этом каждое из них записывается аналогично (1). Так xj Dj будет иметь вид
Р[xj Dj]  i.
i.
Надо сказать, что в практических задачах граничные условия dj , Dj - случайными величинами являются крайне редко, поэтому их запись будем сохранять в виде (2). Объединяя целевую функцию, ограничения и граничные условия, можно сформулировать две постановки задачи стохастического программирования:
М - постановка
M[F] |
max (min) |
|
n |
|
|
P |
aij x j bi |
i , |
j 1 |
|
|
dj xj Dj ; i=1,...,m; j=1,...,n.
P - постановка |
|
||
P[Fmax(min)] |
max |
||
|
n |
|
|
P |
aij x j |
bi |
i , |
|
j 1 |
|
|
dj |
xj Dj |
; i=1,...,m; j=1,...,n. |
|
Обе постановки представляют собой задачи нелинейного программирования.
4. Решение и анализ задач в М-постановке
Задача стохастического программирования в М-постановке непосредственно решена быть не может. Для решения следует перейти к детерминированному эквиваленту. В этом случае целевая функция записывается так:
n |
|
M F |
M [ c j ] x j |
j |
1 |
Детерминированный эквивалент ограничений имеет следующий вид:
n |
|
|
|
M [ aij ] xij t( i ) |
2 [ aij ] x 2j |
2 [ bi ] M [ bi ] , |
(4) |
j 1
где |
i - задаваемый уровень вероятности, с которой должно выполняться i-тое |
|||||||
ограничение; |
|
|
|
|||||
t( i) - вычисляется с помощью функции НОРМСТОБР ( i ). |
||||||||
Введем обозначение |
|
|
||||||
|
|
|
|
|
|
|
|
|
W |
i |
|
2 [ a |
ij |
] x 2 |
2 |
[ b ] |
|
|
|
|
j |
|
i |
|||
Эта величина зависит от разброса значений аij, bi.
В случае детерминированных исходных данных Wi =0 и (4) будет иметь вид детерминированной задачи:
n
aij x j bi
j 1
Из (4) видно, что в задаче распределения ресурсов член t( i) Wi - это величина дополнительного ресурса, который требуется вследствие вероятностных исходных данных. Таким образом, при решении задачи будем пользоваться детерминированным эквивалентом:
|
n |
|
|
|
|
|
M [ c j ] x j |
m a x(m in ) |
|
|
|
j |
1 |
|
|
|
|
|
n |
|
|
|
|
|
|
2 [ aij ] x 2j |
2 [ bi ] M [ bi ] , |
||
|
M [ aij ] xij |
t( i ) |
|||
j |
1 |
|
|
|
|
dj xj Dj ; i=1,...,m; j=1,...,n.
5. Ввод исходных данных для детерминированного эквивалента
Решение задачи стохастического программирования рассмотрим на примере задачи распределения ресурсов.
Примечание. |
|
При вводе исходных данных достаточно часто значения |
[aij], [bi] бывают неизвестны. В этом |
случае можно задать коэффициент вариабильности v(x) = |
[x]/M[x] и, зная который, определить |
[x]= v(x) M[x] |
|
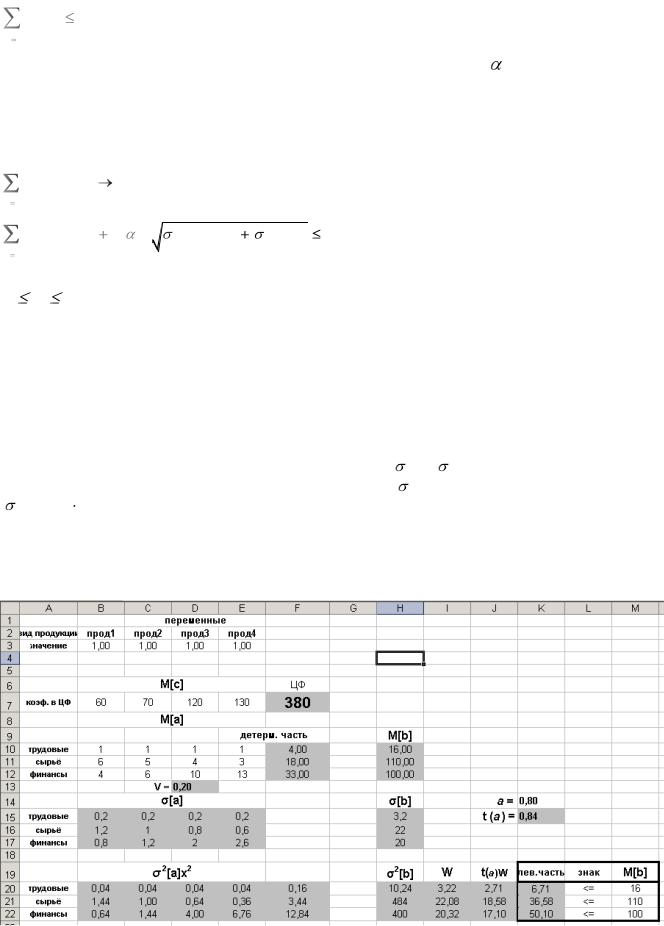
В качестве средних значений принять те значения, которые были в детерминированной задаче. Ввод данных произвести в таблицу, как представлено на рис.4.4.
Рис. 4.4
Примечание:
Ячейки, выделенные цветом, содержат формулы.
6. Решение задачи стохастического программирования
Решение задачи стохастического программирования производится как решение обычной задачи линейного программирования (по алгоритму лабораторной работы № 2).
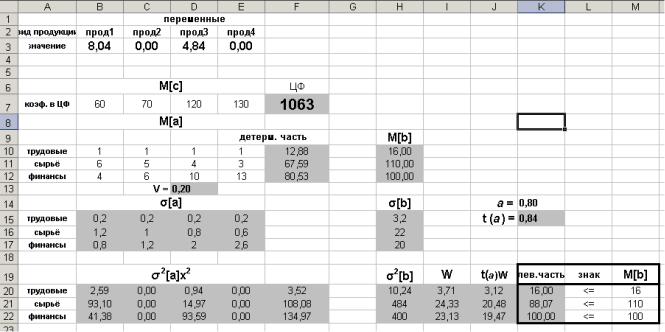
Полученное нецелочисленное решение показано на рис. 4.5.
Рис. 4.5.
7. Решение целочисленной задачи стохастического программирования
Для получения целочисленного решения в диалоговое окно Поиск решения дополнительно ввести: В3: Е3 - целое.
На экране: результат решения (рис.4.6).
