
моделирование / LabNo7
.pdf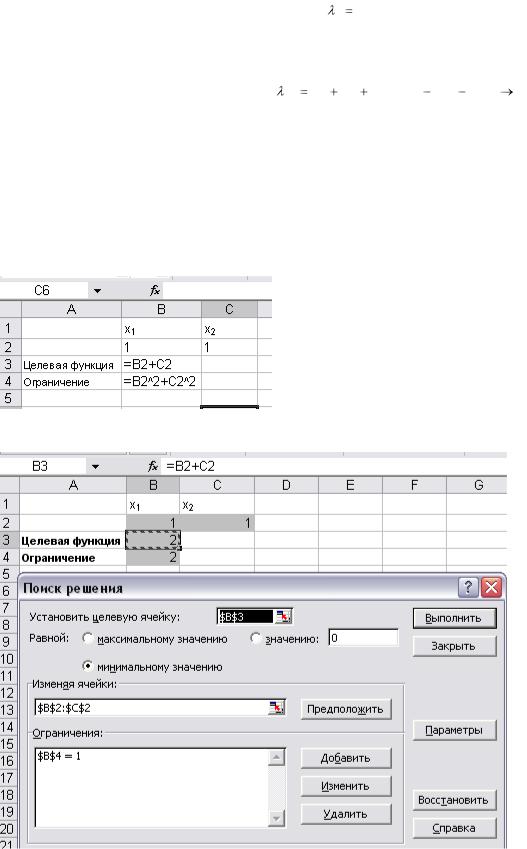
|
1 |
. |
|
|
(5) |
1 |
|
|
|
||
|
2 x1 |
|
|
|
|
5. Подставим (5) в функцию Лагранжа: |
|
|
|
|
|
L ( x1 , x 2 , 1 ) x1 x 2 |
1 / 2 x1 (1 x1 |
2 x 2 |
2 ) min |
(6) |
|
Задача (6) является задачей безусловной оптимизации, решение которой про-
изводится методами, рассмотренными выше.
Возможно следующее решение задачи нелинейного программирования.
Обратимся к предыдущему примеру. Составим форму для ввода условий за-
дачи.
Выполним необходимые действия в окне ПОИСК РЕШЕНИЯ.
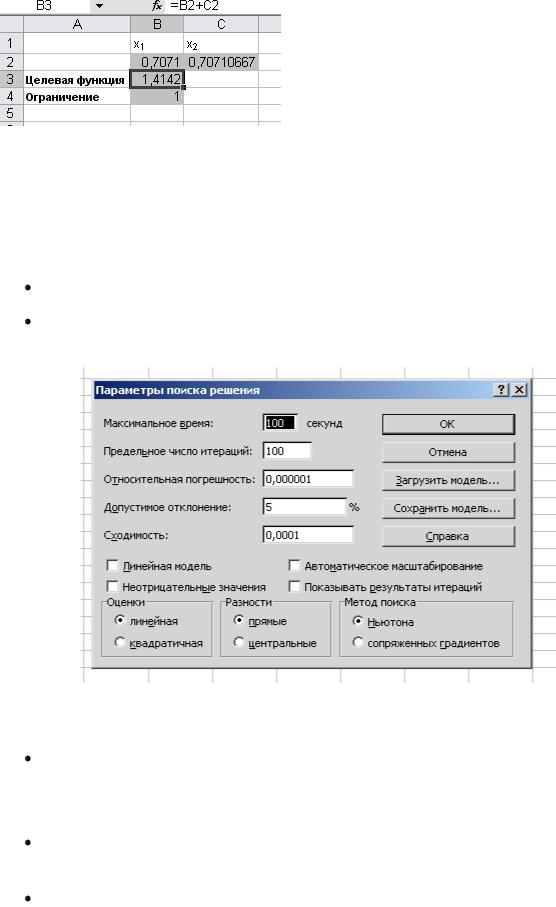
Найденное решение полностью соответствует графической интерпретации поставленной задачи.
Примечание.
Решение задачи нелинейного программирования отличается от решения задачи ли-
нейного программирования следующим:
назначаются начальные значения искомых переменных x j 0 ;
в диалоговом окне Параметры поиска решения не надо вводить Линейная модель.
На экране: диалоговое окно Параметры поиска решения (рис. 6.10).
Рис. 6.10
В этом окне назначаются параметры поиска решения. Отметим следующее:
При поиске оптимального решения смысл этих параметров знать не обязатель-
но, т. к. их значения, применяемые по умолчанию, обеспечивают нормальное решение практических задач.
Все необходимые сведения о параметрах и командах, вводимых в этом диало-
говом окне, можно получить, вызвав Справку.
Основные параметры, смысл которых очевиден, а их назначение не требует специальных знаний, приведены ниже.
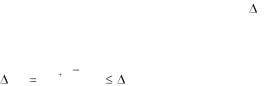
Максимальное время (в секундах). По умолчанию принимается 100. Предельное
число итераций. По умолчанию принимается 100.
Если этих значений для нахождения решения окажется недостаточно, то на экране появится соответствующее сообщение после чего вычисление можно повторить при тех
же параметрax без их повторного назначения.
Относительная погрешность обеспечивает назначение величины Fзад в признаке
достижения оптимального решения
Fk |
Fk 1 |
Fk |
F зад |
Fk |
|
Используемая по умолчанию величина 0,000001, обеспечивает достаточно высокую точность решения. Заметим, что снижение точности уменьшает число итераций и сокра-
щает время поиска решения.
Говоря о назначении метода решения, можно отметить, что нет методов лучших и худших, т. к. применение того или иного метода поиска оптимального решения зависит от типа нелинейности. При этом, как мы уже отмечали, в методе Ньютона используются вто-
рые производные, что требует больших вычислений на каждой итерации, но оптимальное решение находится за меньшее число итераций, чем в градиентных методах, в которых используются первые производные.
Анализ оптимального решения
После успешного завершения поиска оптимального решения на экране появ-
ляется диалоговое окно Результаты поиска решения.
С помощью этого диалогового окна можно вызвать отчеты трех типов:
 результаты;
результаты;
 устойчивость;
устойчивость;
 пределы.
пределы.
Отчеты анализа по результатам и пределам аналогичны таким же отчетам для задач линейного программирования. Они не содержат новой информации,
которой бы не было при представлении результатов решения, поэтому мы их рассматривать не будем. Отчет по устойчивости, который отличается от от-
чета по устойчивости для задачи линейного программирования, Вам необхо-
димо проанализировать самостоятельно.
Варианты заданий

Задана функция вида (x) = a |
x 2 |
a |
x x |
2 |
a |
22 |
x 2 |
b x |
b |
x |
2 |
. |
|
11 |
1 |
12 |
1 |
|
2 |
1 |
1 |
2 |
|
|
|||
1.Найти экстремум и определить его тип (max или min) для заданной функции (x) классическим методом, используя необходимые и достаточные условия существования экстремума.
2.Задать начальную точку и выполнить четыре шага градиентным методом.
3.Задать начальную точку и выполнить три шага методом наискорейшего спуска.
4.Задать начальную точку и выполнить один шаг методом Ньютона.
5.Дать графическую иллюстрацию каждого метода.
6.Решить задачу, используя процедуру ПОИСК РЕШЕНИЯ.
Значения a11, a12, a22, b1, b2 |
приведены в таблице. |
||||
|
|
|
|
|
|
Номер |
a11 |
a12 |
a22 |
b1 |
b2 |
варианта |
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
-2 |
2 |
-1 |
3 |
|
|
|
|
|
|
2 |
1 |
2 |
2 |
3 |
1 |
|
|
|
|
|
|
3 |
2 |
-2 |
1 |
-1 |
3 |
|
|
|
|
|
|
4 |
2 |
2 |
1 |
-3 |
1 |
|
|
|
|
|
|
5 |
3 |
2 |
2 |
2 |
-1 |
|
|
|
|
|
|
6 |
3 |
-2 |
2 |
3 |
-2 |
|
|
|
|
|
|
7 |
1 |
-1 |
1 |
3 |
-2 |
|
|
|
|
|
|
8 |
1 |
1 |
1 |
4 |
-1 |
|
|
|
|
|
|
9 |
2 |
-2 |
1 |
2 |
-3 |
|
|
|
|
|
|
10 |
2 |
2 |
1 |
4 |
-1 |
|
|
|
|
|
|
11 |
1,5 |
1 |
1 |
1 |
2 |
|
|
|
|
|
|
12 |
1,5 |
-1 |
1 |
-1 |
2 |
|
|
|
|
|
|
13 |
1,5 |
1 |
1,5 |
2 |
-3 |
|
|
|
|
|
|
14 |
1,5 |
-2 |
1,5 |
2 |
4 |
|
|
|
|
|
|
15 |
1,5 |
2 |
2 |
2 |
-1 |
|
|
|
|
|
|
Контрольные вопросы
1.Что означают и чем отличаются понятия «оптимум» и «экстремум»?
2.Какие методы решения задач нелинейного программирования вы знае-
те?
3.В чем заключается идея метода неопределенных множителей Лагран-
жа?
4.Что представляет собой функция Лагранжа?
5.Приведите алгоритм решения задачи нелинейного программирования методом неопределенных множителей Лагранжа.
6.Каким образом можно интерпретировать множители Лагранжа?
7.Какое требование является обязательным при выборе начальных зна-
чений искомых переменных?
Литература
1.Акулич И. Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. спец. вузов. - М.: Высш. шк., 1986. -
319с.
2.Волкова Т.Б., Диканова Л.С., Журина Н.Э. и др. Методы оптимизации в экономике: Методические указания к курсовым работам - М.: Изд-во МАИ,
1994.- 52с.: ил.
3.Мастяева И.Н., Горбовцов Г.Я., Турундаевский В.Б. Методические указания и задания по курсам: прикладная математика и математическое моделирование в бизнесе: Учебное пособие.- М.: Изд-во МЭСИ, 1996.
4.Курицкий Б.Я. Поиск оптимальных решений средствами Excel 7.0 - СПб.: BHV - Санкт-Петербург, 1997. - 384с., ил.
5.Орлова И.В. Экономико-математические методы и модели. Выполнение расчетов в среде EXCEL / Практикум: Учебное пособие для вузов. – М.: ЗАО «Финстатинформ», 2000.- 136с.
6.Куликов Ю.Г., Шеховцова Н.Ф., Зикеева Л.П. Экономико-математические методы и модели (раздел «Линейное программирование»): Учебное пособие для практических занятий. – М.: Московский психолого-социальный институт; Воронеж: Издательство НПО «МОДЭК», 2000.- 96с. (Серия «Библиотека экономиста»).
7.Кузнецова М.В. Моделирование экономических процессов / Учебнометодическое пособие.- Пенза: Изд-во ПТИ, 2000,49с., 6 ил., 23 табл., библиогр. 7 назв.
8.Кузнецова М.В. Математическое программирование: Учеб. пособие. / Пенза: изд-во ПГТА, 2004.- 150с.
