3.3.1.3.2. Метод Ньютона

Требуется решить уравнение , причемиопределены, непрерывны и сохраняют постоянные знаки на отрезке

Рассмотрим геометрическую интерпретацию метода Ньютона (рис. 3.7).

1)  Выбираем –начальное приближение корня x*. При этом надо придерживаться следующего правила:

за начальное приближение корня следует принять тот конец отрезка , в котором знак функции совпадает со знаком второй производной, т.е. выполняется условие:

(3.23)

Это условие сходимости метода Ньютона.

Основываясь на свойствах данной функцииf(x) (см. рис. 3.4), делаем вывод: условие сходимости выполняется для точки , поэтому принимаем

2) Вычисляем значение функции . Проводим касательную к кривойв точке. Абсцисса точки пересечения касательной с осью Оx принимается за новое (первое) приближение корня x₁.

Известно, что уравнение касательной, проведенной в точке B₀ с координатами (x_0, f(x₀)) к кривой функции f(x), имеет вид:

(3.24)

где x, y – текущие координаты точки, лежащей на касательной.

Для точки x₁ сделаем подстановку в уравнение касательной (3.24):

x = x₁; (3.25)

(3.26)

получаем:

. (3.27)

Обе части уравнения (3.27) делим на и выражаемx₁:

(3.28)

3) Вычисляем значение функции в точкеx₁, проводим касательную к кривой в точкеАбсцисса точки пересечения касательной с осью Оx представляет собой второе приближение корня x₂:

(3.29)

4) Продолжаем последовательно проводить касательные и определять точки их пересечения с осью Оx. Тогда для текущего k-го приближения корня итерационный процесс реализуется рекуррентной формулой:

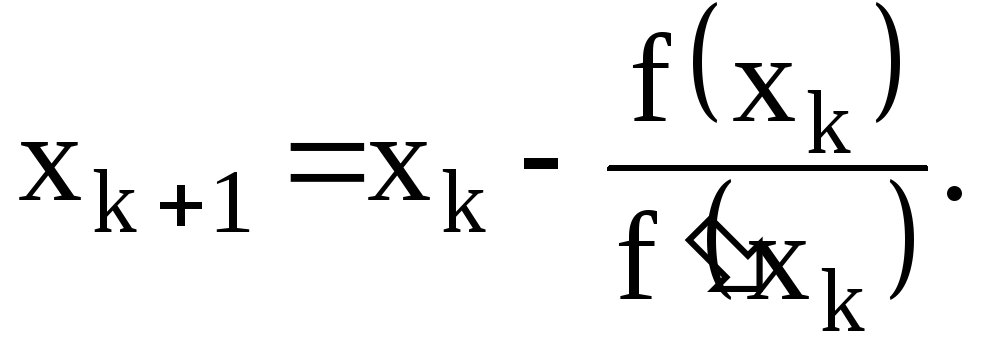(3.30)

Процесс уточнения корня прекращается, когда выполнится условие близости двух последовательных приближений:

(3.31)

Алгоритм, реализующий метод Ньютона, представлен на рис. 3.8.

Блок 4 реализует проверку условия сходимости метода и выбор значения начального приближения (блоки 5, 6).

Блок 10 реализует подсчет количества итераций, 11 – вычисление текущего приближения корня через предыдущее приближение.

Метод Ньютона обладает высокой скоростью сходимости, которая тем выше, чем больше крутизна графика функции в пределах рассматриваемого отрезка. Если численное значение производноймало вблизи корня, то процесс уточнения корня может оказаться очень долгим.

Неудачно выбранное начальное приближение может привести к расходимости метода (см. рис. 3.7): представим, что за начальное приближение x₀ принят левый конец отрезка a, касательная, проведенная в точке А₀, пересекает ось Оx за пределами заданного отрезка [a,b]. Таким образом, получили первое приближение к корню ‹x₁›, еще дальше отстоящее от искомого значения корня x*, чем нулевое приближение .