
- •Тема 3. Математические модели в форме нелинейных алгебраических и трансцендентных уравнений и методы их решения
- •3.1. Пример формирования модели
- •3.2. Базовые понятия
- •3.3. Методы решения
- •3.3.1. Особенности численных методов решения
- •3.3.1.1. Этапы численного решения нелинейного уравнения
- •3.3.1.2. Отделение корней
- •3.3.1.3. Уточнение корней
- •3.3.1.3.1. Метод половинного деления (дихотомии, бисекции)
- •3.3.1.3.2. Метод Ньютона
- •3.3.1.3.3. Метод итерации
- •3.4. Решение нелинейных алгебраических и трансцендентных уравнений в среде MathCad
- •Информация к решению
- •Фрагмент рабочего документа MathCad
- •Фрагмент рабочего документа MathCad
- •Фрагмент рабочего документа MathCad
- •Фрагмент рабочего документа MathCad
3.3.1.3. Уточнение корней
Рассмотрим два численных метода уточнения корней, применяемых для решения как алгебраических, так и трансцендентных уравнений. Эти методы относятся к разряду итерационных.
Итерационный процесс состоит в последовательном шаг за шагом уточнении начального приближения x0 искомого корня. Каждый шаг такого метода называется итерацией.
В
результате реализации итерационного
метода получают последовательность
приближенных значений корня
![]() Если эти значения с увеличением n
приближаются к истинному значению
корня x*, то говорят, чтоитерационный
процесс сходится.
Если эти значения с увеличением n
приближаются к истинному значению
корня x*, то говорят, чтоитерационный
процесс сходится.
3.3.1.3.1. Метод половинного деления (дихотомии, бисекции)
Пусть дано уравнение
![]() (3.17)
(3.17)
где
функция
![]() непрерывна и монотонна на отрезке
непрерывна и монотонна на отрезке![]() и имеет на концах отрезка разные знаки:
и имеет на концах отрезка разные знаки:
![]() (3.18)
(3.18)
Требуется
найти корень
![]() уравнения(3.17)
с
точностью до
уравнения(3.17)
с
точностью до
![]()
График
функции
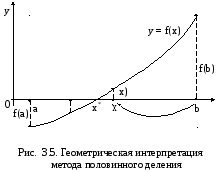
![]() представлен на рис. 3.5.
представлен на рис. 3.5.
Рассмотрим суть и этапы реализации метода половинного деления.
1)
Отрезок
![]() делим пополам и определяем середину
отрезка:
делим пополам и определяем середину
отрезка:
![]() (3.19)
(3.19)
2)
Вычисляем значение функции в точке
![]() Если
Если![]() ,
то
,
то![]() является корнем уравнения. Если
является корнем уравнения. Если![]() то поиск корня продолжается на одном
из двух полученных отрезков –
то поиск корня продолжается на одном
из двух полученных отрезков –![]() или
или
![]() .
.
Следует
выбрать тот отрезок, на концах которого
функция
![]() принимает значения противоположных
знаков.
принимает значения противоположных
знаков.
В
данном случае (см. рис. 3.5) выбираем
отрезок
![]() ,
так как для него выполняется условие:
,
так как для него выполняется условие:
![]() Для того чтобы сохранить в дальнейших
расчетах единое обозначение
Для того чтобы сохранить в дальнейших
расчетах единое обозначение
![]() текущего отрезка, на котором ведется
поиск корня на данном шаге вычислений,
необходимо параметруb
присвоить новое значение
текущего отрезка, на котором ведется
поиск корня на данном шаге вычислений,
необходимо параметруb
присвоить новое значение
![]() :
b
=
:
b
=
![]() .
С точки зрениягеометрической
интерпретации
(см. рис. 3.5) это означает, что правая
граница исходного отрезка точка b
переносится в точку
.
С точки зрениягеометрической
интерпретации
(см. рис. 3.5) это означает, что правая
граница исходного отрезка точка b
переносится в точку
![]() а оставшаяся за пределами точки
а оставшаяся за пределами точки![]() часть графика дальше не рассматривается.
часть графика дальше не рассматривается.
3)
Новый отрезок
![]() снова
делим пополам:
снова
делим пополам:
![]()
 (3.20)
(3.20)
4)
Вычисляем
![]() ипроводим
анализ двух вновь полученных отрезков
–
ипроводим
анализ двух вновь полученных отрезков
–
![]() и
и
![]() .
Выбираем
тот из них, для которого выполняется
условие противоположности знаков
функции в граничных точках.
.
Выбираем
тот из них, для которого выполняется
условие противоположности знаков
функции в граничных точках.
5)
Процесс
деления пополам текущего отрезка
продолжаем до тех пор, пока очередной
отрезок
![]() не будет удовлетворять условию:
не будет удовлетворять условию:
![]() (3.21)
(3.21)
где ε – требуемая точность расчета.
За
приближенное значение корня x*
принимаем
значение середины последнего отрезка
![]() ,
т. е.
,
т. е.
x*
= ![]() .
(3.22)
.
(3.22)
При
этом погрешность вычисления корня
не будет превышать
![]() ,
гдеn
– количество произведенных делений
отрезков (количество итераций).
,
гдеn
– количество произведенных делений
отрезков (количество итераций).
Алгоритм метода половинного деления, представлен на рис. 3.6.
В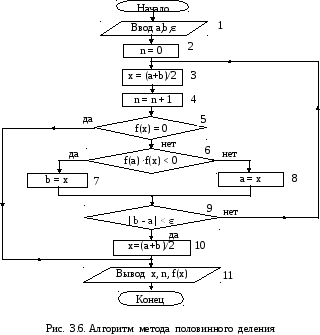 блоке 2 (рис. 3.6) задается начальное
значение счетчикаn
количества итераций (делений отрезка
блоке 2 (рис. 3.6) задается начальное
значение счетчикаn
количества итераций (делений отрезка
![]() пополам). Блоки 6 – 8 реализуют выбор
того из двух отрезков, на котором следует
продолжать поиск корня и соответственно
корректировку границы (b
–
при выборе левого отрезка, a
–
правого).
пополам). Блоки 6 – 8 реализуют выбор
того из двух отрезков, на котором следует
продолжать поиск корня и соответственно
корректировку границы (b
–
при выборе левого отрезка, a
–
правого).
Метод половинного деления – один из самых простых и надежных. Сходимость метода обеспечена для любых непрерывных функций, в том числе и для недифференцируемых.
Метод устойчив к ошибкам округления. Однако скорость сходимости его меньше, чем у методов Ньютона и итерации.
