2.5. Расчет теплового состояния ад

Непосредственный расчет теплового режима электрической машины представляет собой сложную многофакторную задачу, решить которую можно лишь при детальном конструктивном расчете. В данной работе рассмотрим этот вопрос с качественной стороны, введя ряд допущений.

Одним из таких допущений будет представление АД однородным телом с равномерно распределенными внутри его объема источниками тепла, которыми в данном случае являются потери.

Процесс нагревания такого тела описывается уравнением:

(68)

где – начальное превышение температуры машины;

–установившееся превышение температуры;

–постоянная времени нагревания.

Если принять установившееся превышение температуры в номинальном режиме равным допустимому для данного класса термостойкости изоляции, то для любого иного режима

, (69)

где – потери наi-й ступени нагрузки, рассчитываются по формуле (63);

–потери в номинальном режиме, вычисляются по уравнению (60);

–допустимое превышение температуры, в данном случае = 80^○ С.

Ориентировочные значения постоянной времени нагревания указаны в прил. 2. За начальное превышение температуры каждой ступени, включая паузу, следует принимать конечное превышение, рассчитанное в конце предыдущей ступени. В начале расчета С.

С целью сокращения времени на расчеты допускается вычислять пре-вышение температуры только в начале и конце каждой ступени без промежу-точных точек. Расчет ведется для нескольких циклов, пока превышения темпе-ратуры не стабилизируются на каждой ступени. По числу циклов можно судить об общем времени нагревания двигателя до установившегося теплового состояния.

Кривые изменения температурного режима показаны на рис. 8. Пункти-ром нанесена обобщенная кривая нагревания, рассчитанная по средним потерям для нескольких значений t:

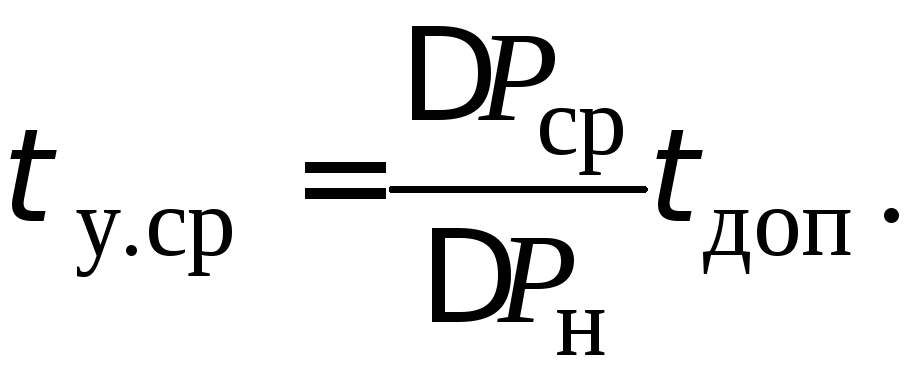(70)

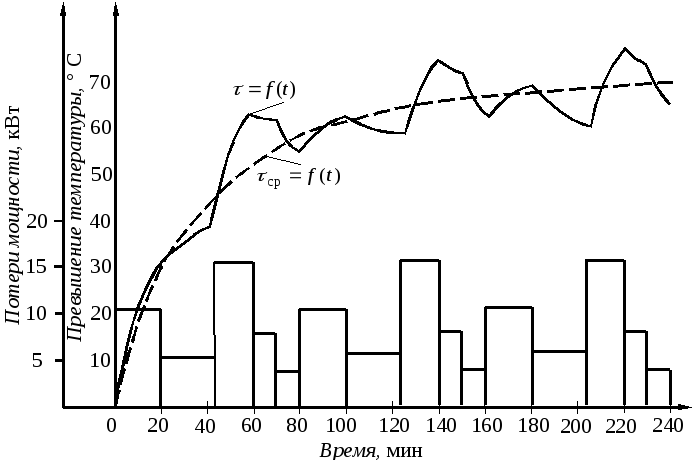
Рис. 8. Кривые нагрева двигателя и диаграмма потерь мощности

2.6. Расчет механических характеристик

Механическими характеристиками АД называют зависимости илипоказанные на рис. 9. В некоторых источниках зависимостьназывают характеристикой электромагнитного момента.

Аналитические выражения данных характеристик достаточно сложны, требуют знания многих параметров АД и для практических целей используются редко. Более удобной является так называемая формула Клосса, вполне удовлетворительно описывающая реальную характеристику в пределах измене-ния скольжения от нуля до критического . Вторая (нерабочая) часть характе-ристики, рассчитанная по формуле Клосса, существенно отличается от реаль-ной, однако на этой части асинхронные двигатели не работают и практи-ческого значения для анализа задач электропривода она не представляет.

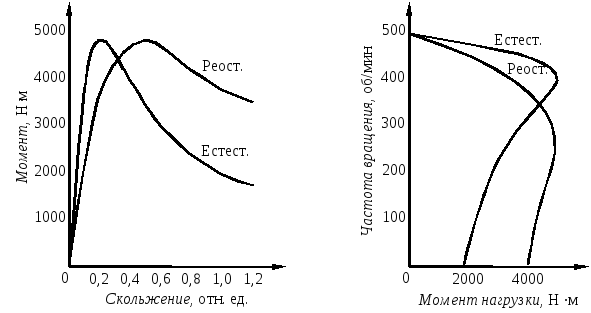
а б

Рис. 9. Механические характеристики АД

При выполнении данной работы можно воспользоваться упрощенной формулой Клосса:

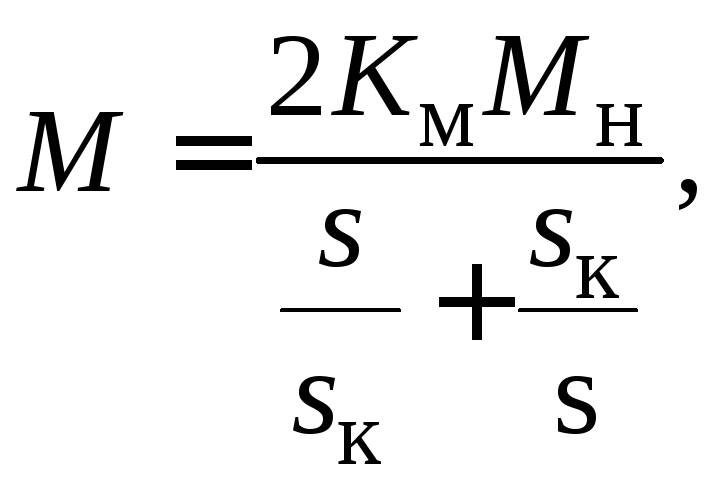(71)

где – коэффициент перегрузочной способности;

–номинальный момент на валу двигателя, рассчитывается по уравнению (9);

–критическое скольжение;

–текущее значение скольжения.

Номинальная частота вращения

(72)

где n₁ – синхронная частота вращения, об/мин;

–номинальное скольжение по каталогу, отн. ед.

Критическое скольжение, соответствующее максимальному моменту, может быть найдено по формуле (71):

(73)

Определив критическое скольжение по уравнению (73) и задавшись величиной скольжения от нуля до 1,2, по формуле (71) можно рассчитать зависимость, которую затем легко перевести в координатыпо формуле:

(74)

Характеристики, рассчитанные таким образом, при отсутствии резисторов в цепи ротора называются естественными.

Введение добавочного сопротивления в цепь ротора приводит к увеличению критического скольжения, величина максимального момента при этом не изменяется. Иными словами, механическая характеристика смещается вниз, а– вправо. В этом случае при постоянном моменте сопротивлениячастота вращения несколько снижается. При этом соблюдается соотношение:

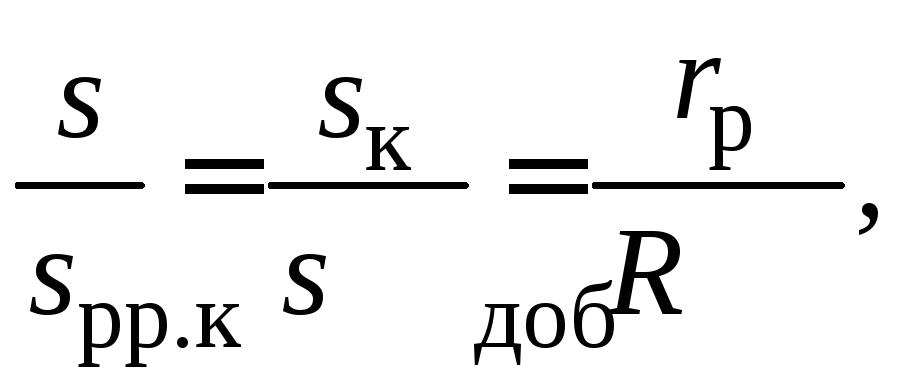(75)

где – скольжение на естественной и реостатной характеристиках;

–критические скольжения на тех же характеристиках;

–сопротивление ротора АД при работе на естественной характеристике, Ом

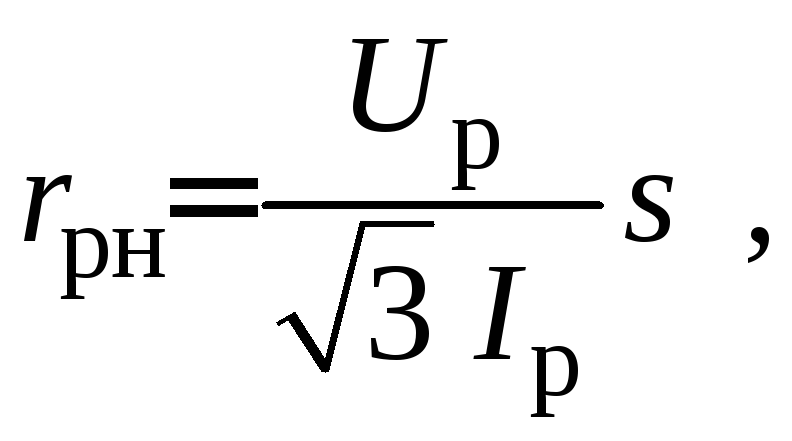(76)

где – напряжение и ток ротора по каталогу;

–добавочный резистор в цепи ротора.

Частота вращения ротора при работе АД на реостатной характеристике может быть найдена при номинальной нагрузке и заданном по формуле:

(77)

а соответствующее ей скольжение –

(78)

Величину добавочного сопротивления, которое необходимо включить в цепь ротора для достижения заданного снижения частоты вращения, легко найти на основании соотношения (75):

(79)

Рассчитать и построить реостатную характеристику можно также по формуле Клосса (71), заменив на, которое в соответствии с формулой (75) вычисляется по уравнению:

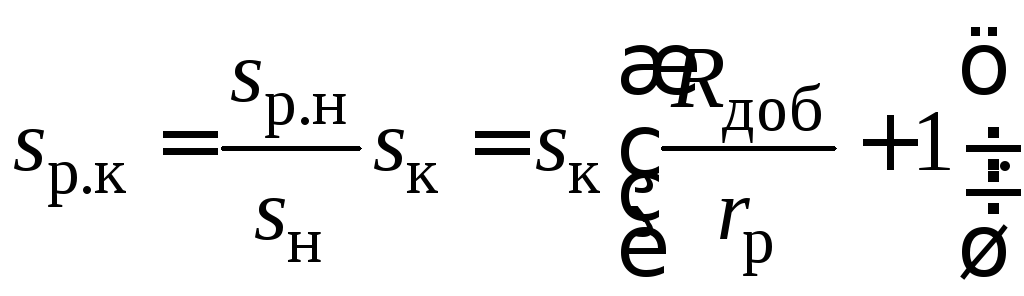(80)

При расчетах механических характеристик следует обязательно задать значение  или, а также ближайшее значениеили. Это позволит четко построить механические характеристики в области перехода их от рабочей части к нерабочей.