Периодичность функций

Функция называетсяпериодической, если существует такое число , что для любого значениях из области определения выполняется равенство

,

число Т называется периодом функции.

Примеры периодических функций: ,,,.

Заметим, что периодическую функцию достаточно исследовать в пределах одного периода, т.е. при .

Пример. Найти наименьший период функции .

Решение. Период для функций иравен. Функцияимеет период в 3 раза меньше, т.е.,. Наименьший период суммыдолжен быть таким, чтобыипомещались в нем целое число раз. В данном случае.

Задание 3. Найти наименьший период функции

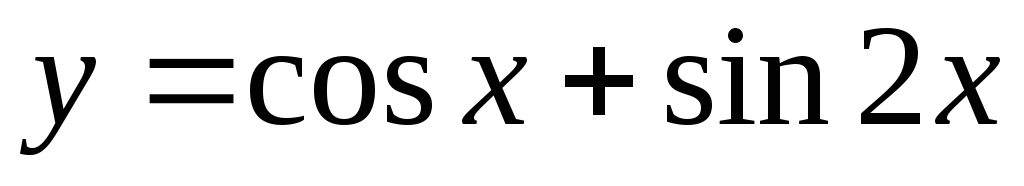
1)	16)
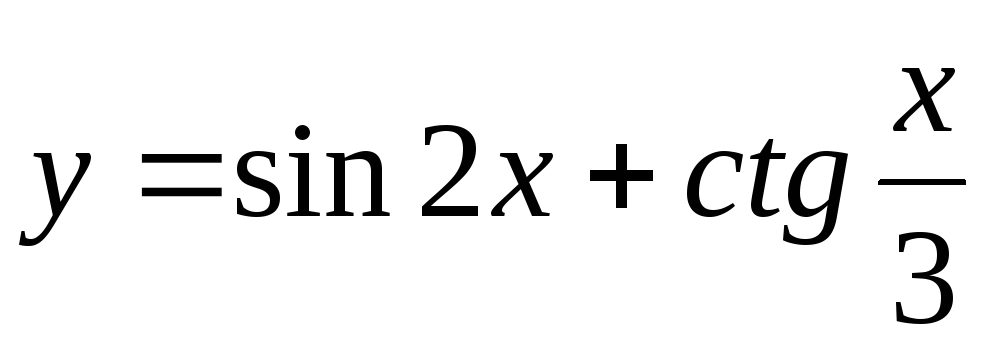
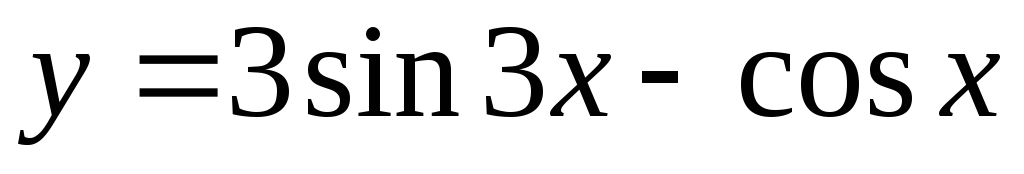
2)	17)
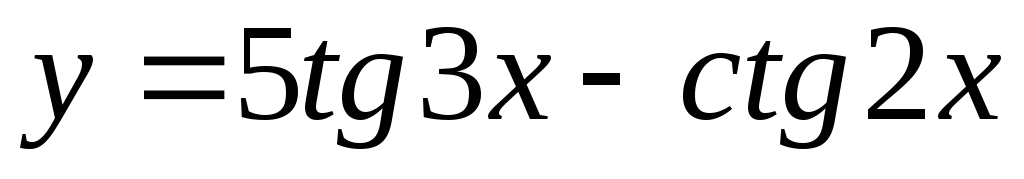
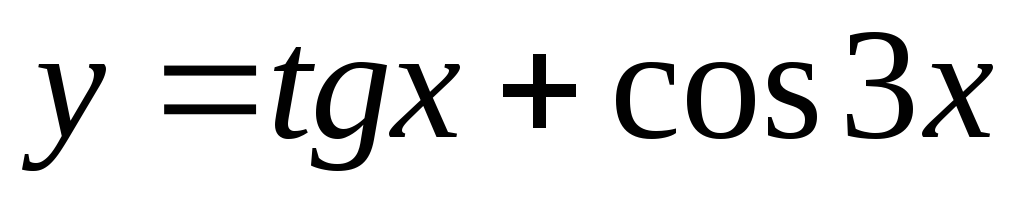
3)	18)
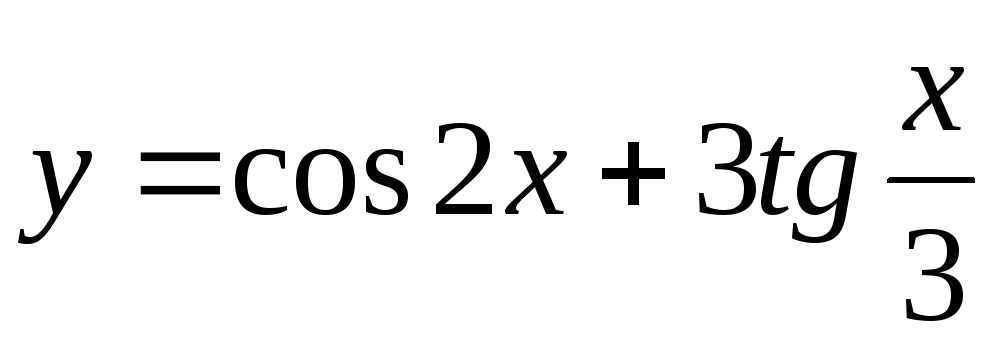
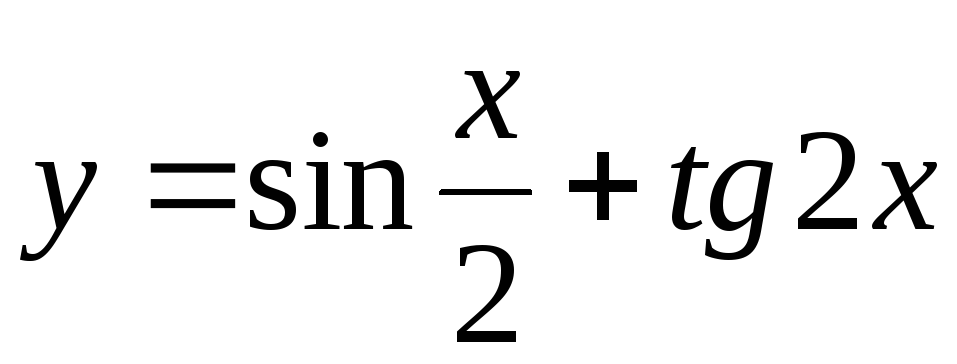
4)	19)
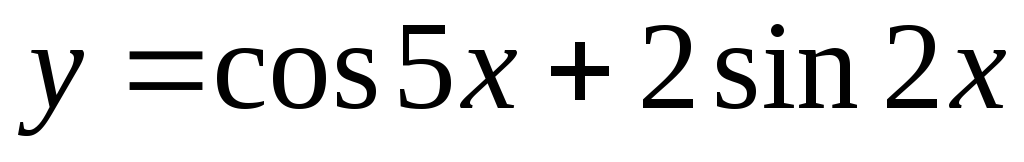
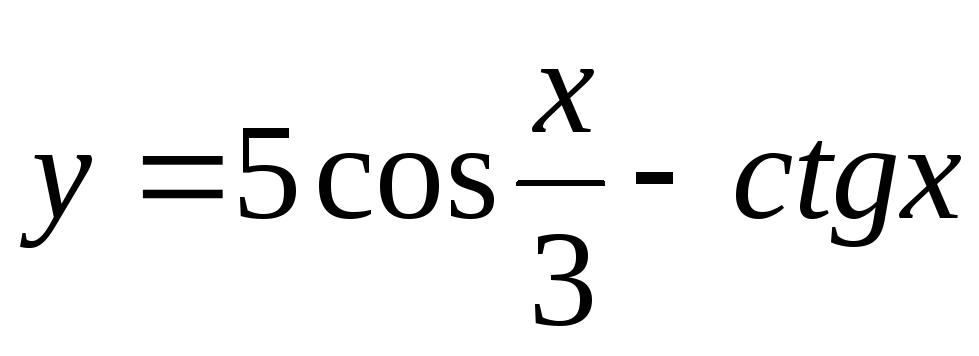
5)	20)
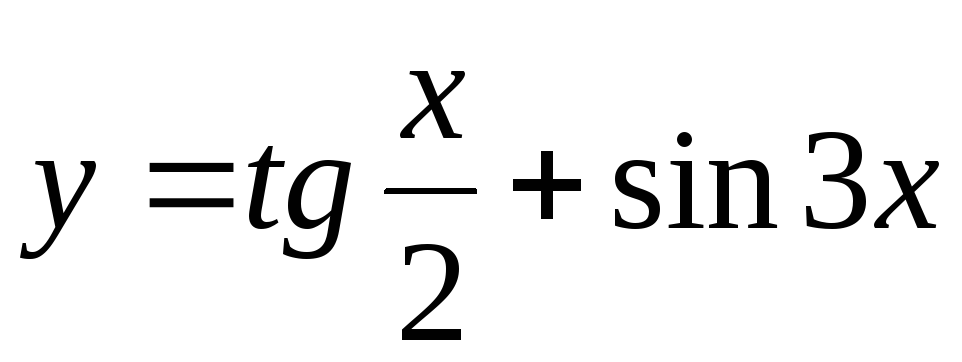
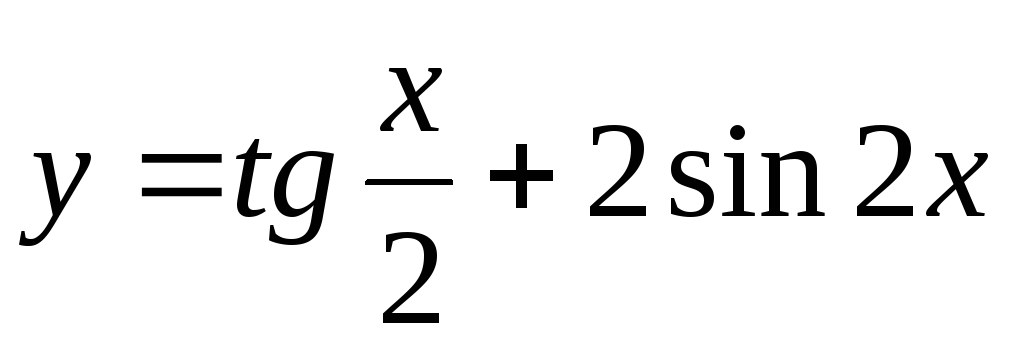
6)	21)
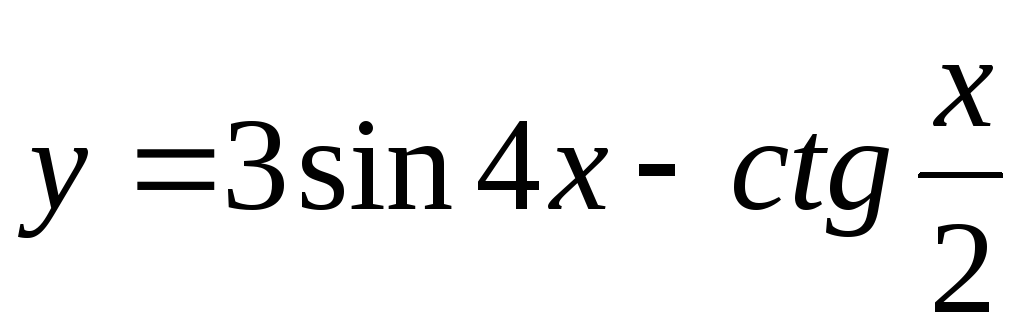
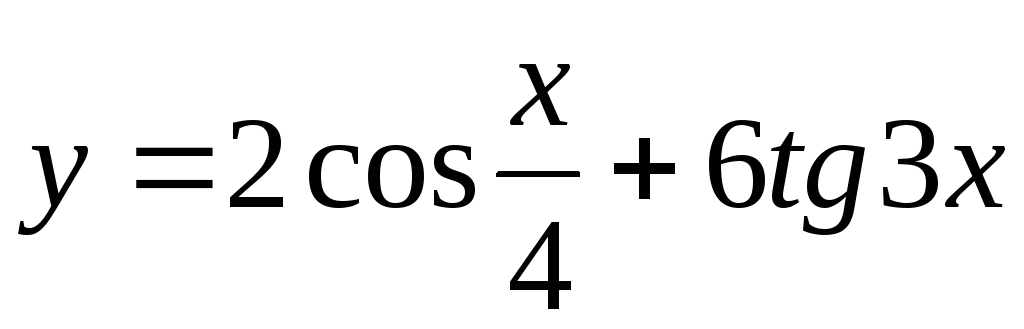
7)	22)
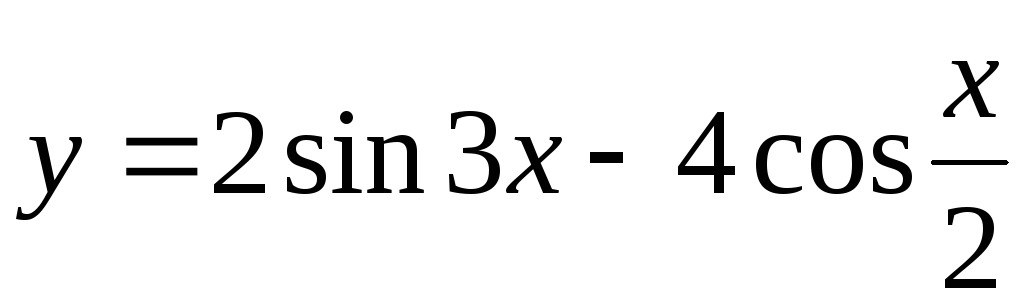
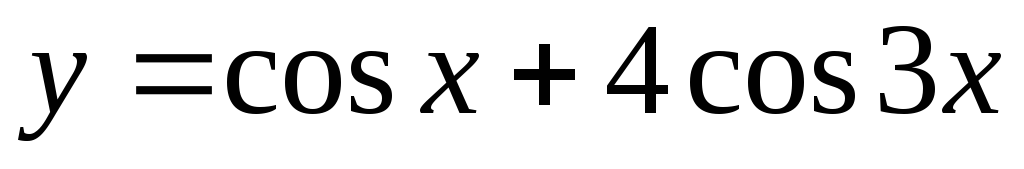
8)	23)
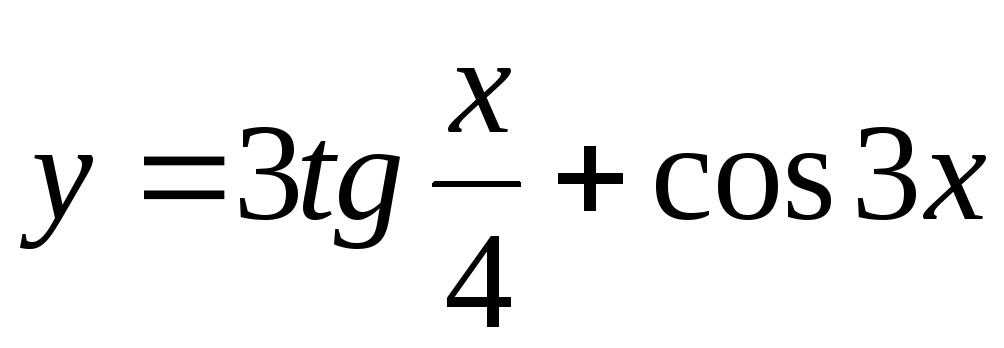
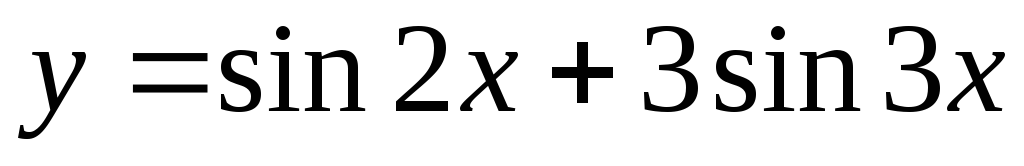
9)	24)
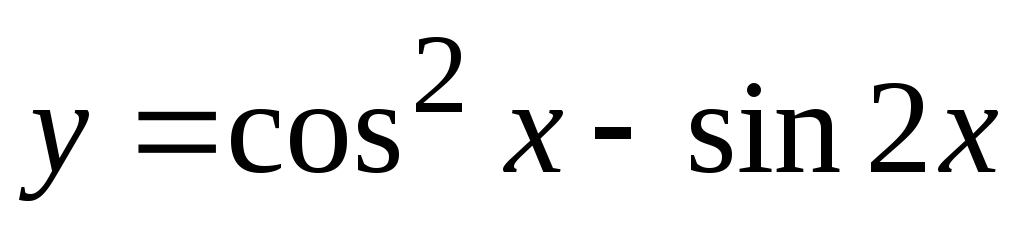
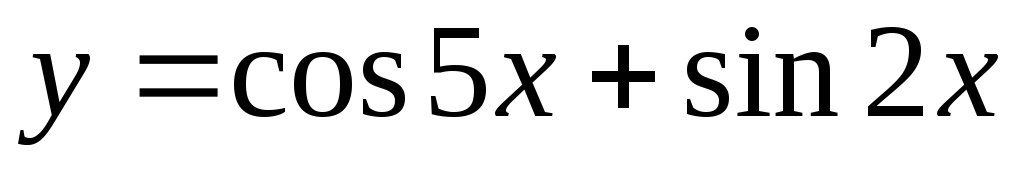
10)	25)
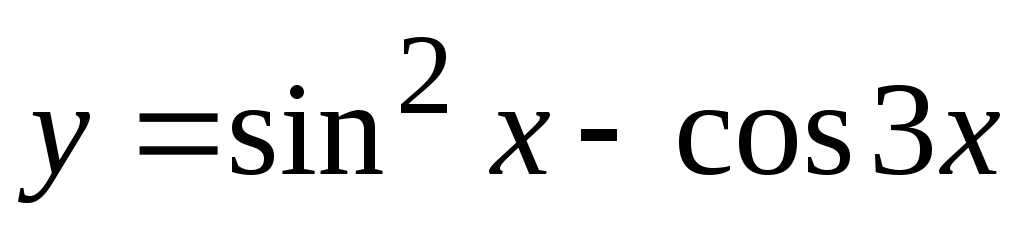
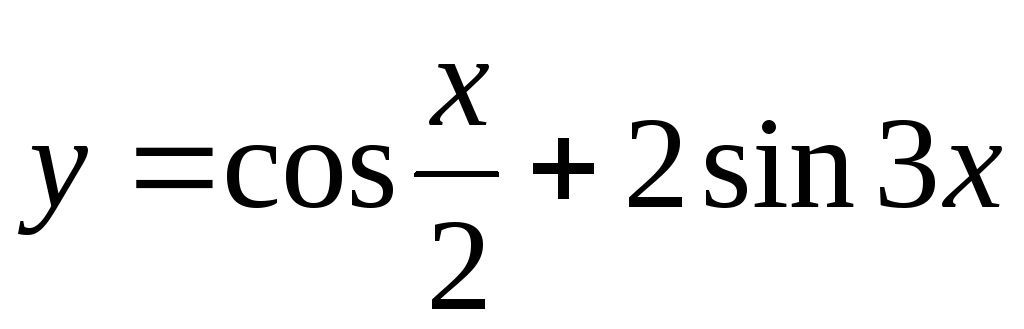
11)	26)
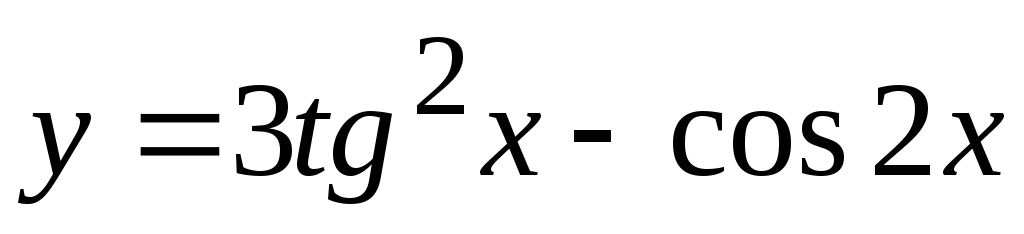
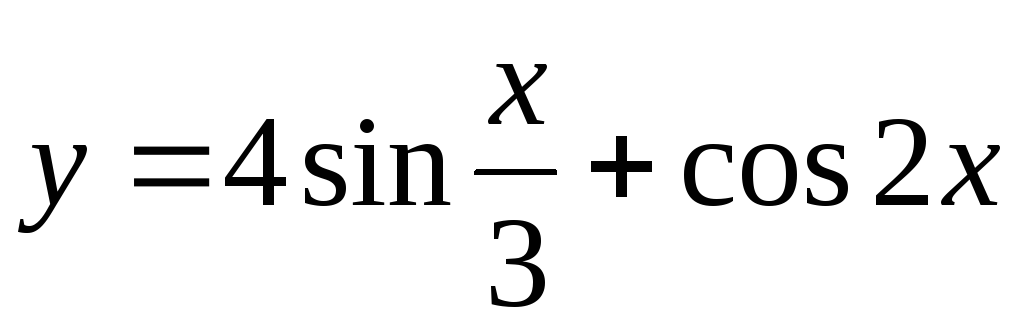
12)	27)
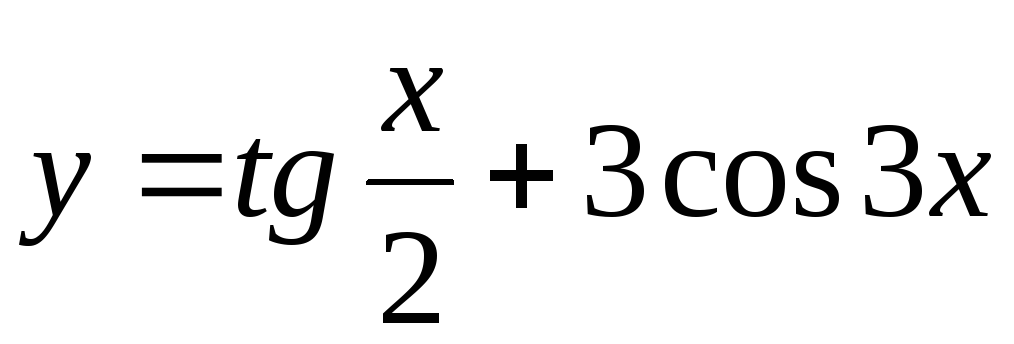
13)	28)
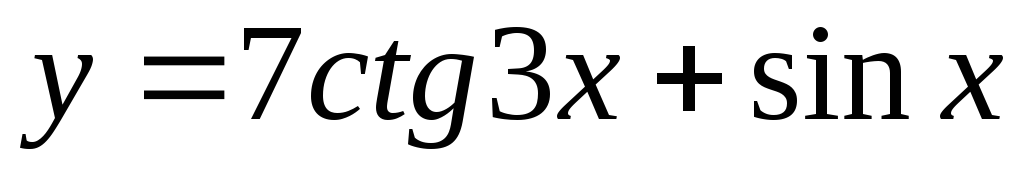
14)	29)
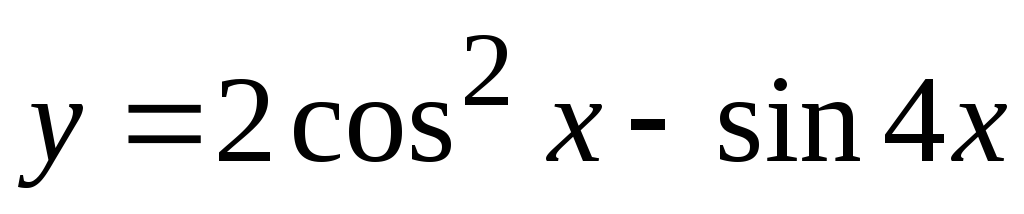
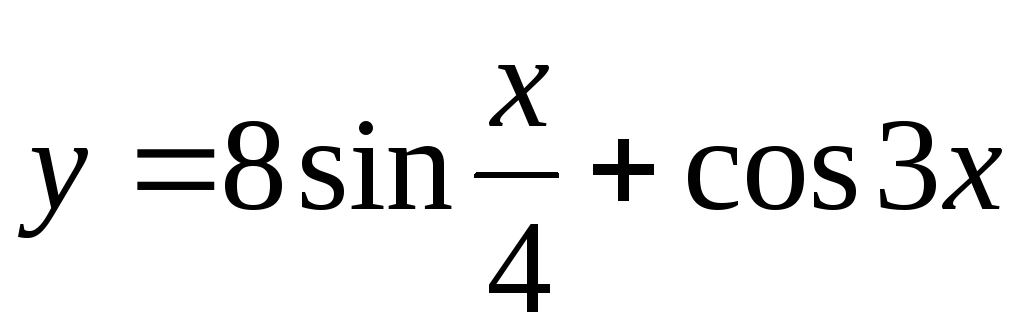
15)	30)

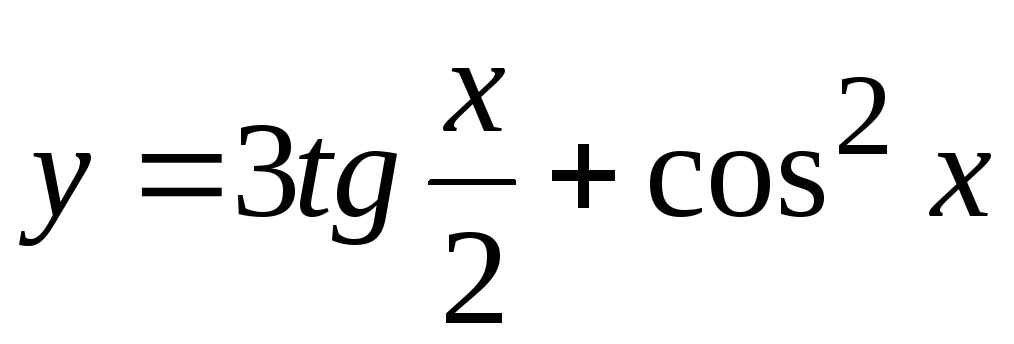
Простейшие преобразования графиков

Пусть в данной системе координат вычерчен график некоторой функции

Из этого графика с помощью специальных приемов легко получить график сходных функций; таких как

,

а также более общего вида

,

где - некоторые константы.

1. График функции 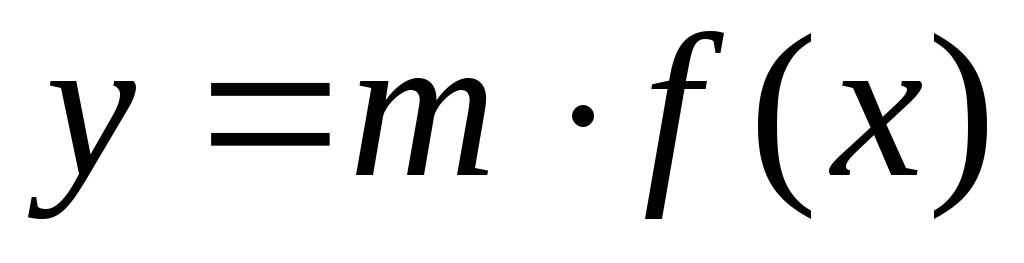получается растяжением 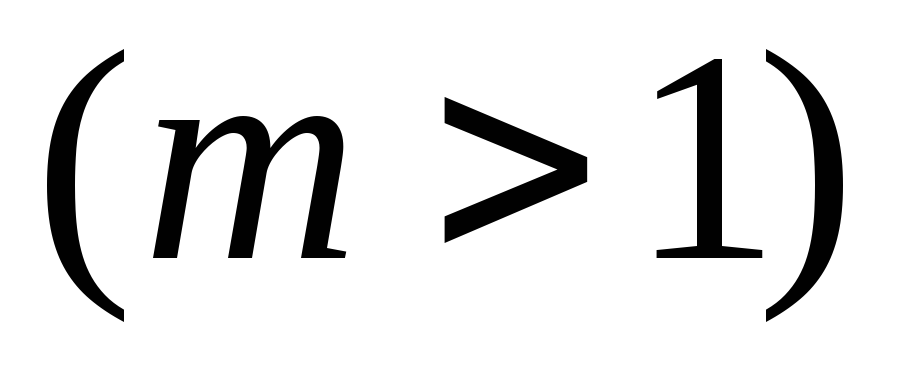или сжатием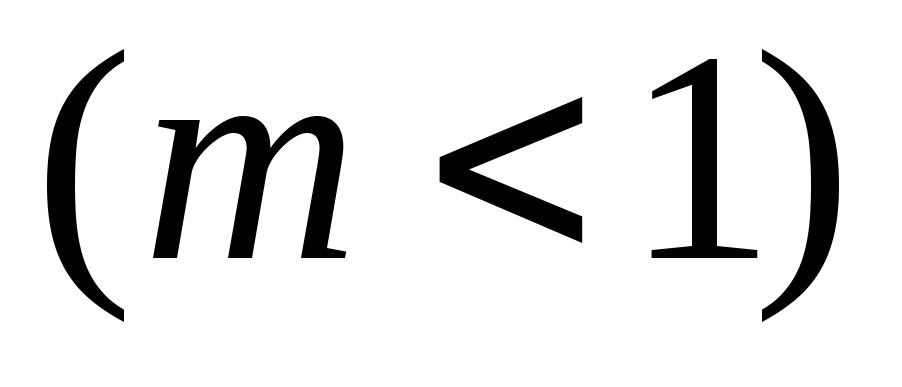вm раз исходного графика вдоль оси Оy.

Если же , то, построив сначала график функции, затем строим симметричный с ним относительно осиОх искомый график функции .

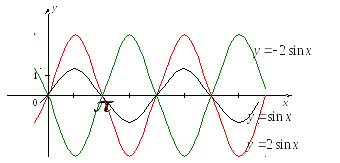
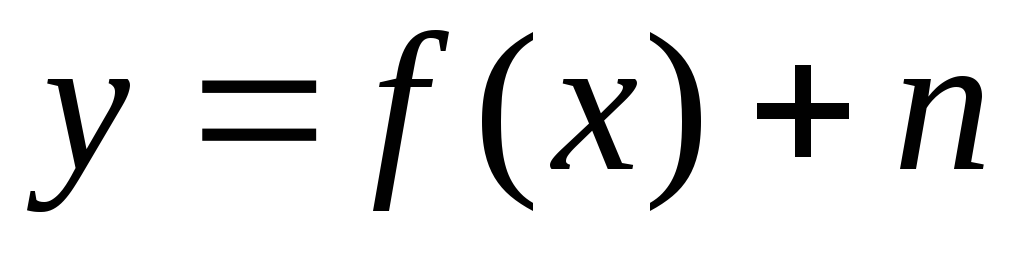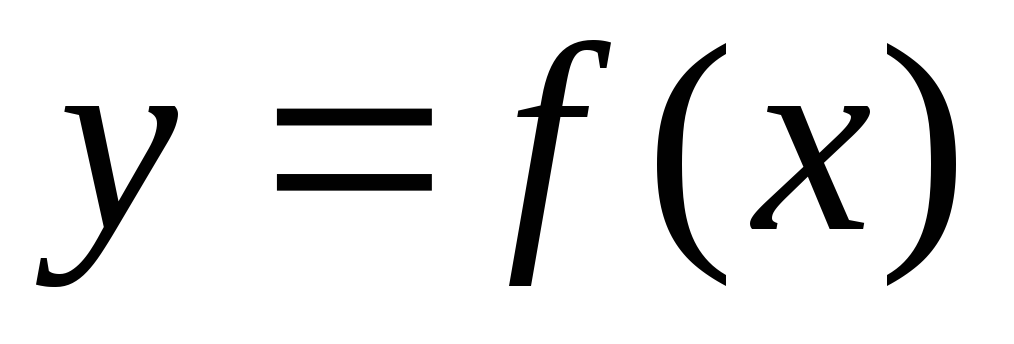2. График функции получается с помощью параллельного переноса (сдвига) графика вдоль осиОy вверх 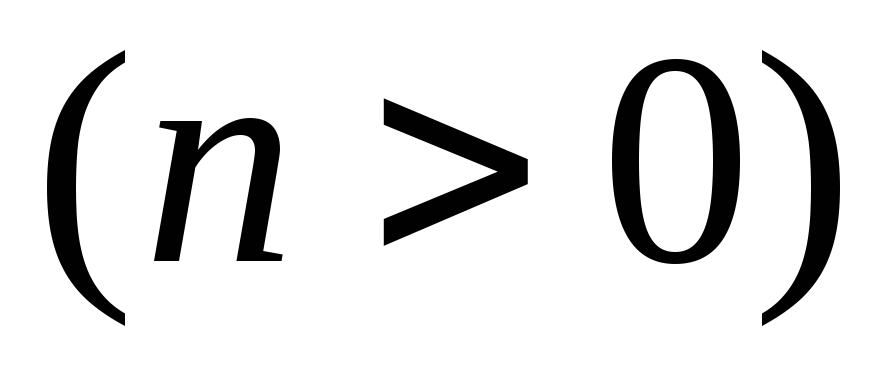или вниз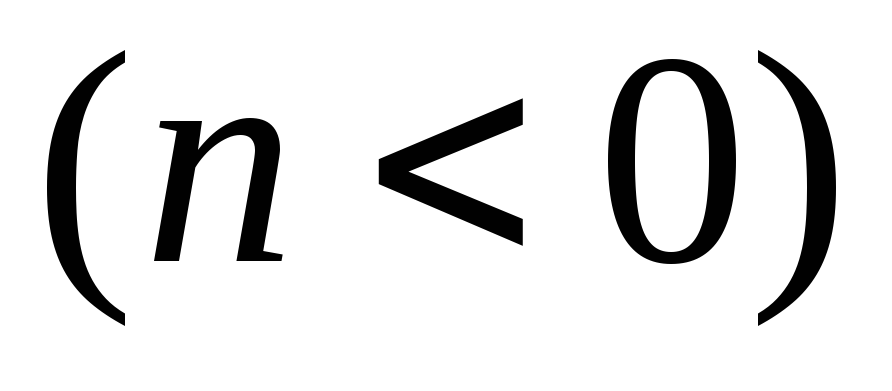наn единиц.

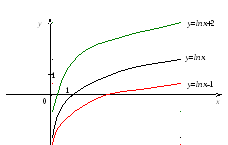
3. График функции 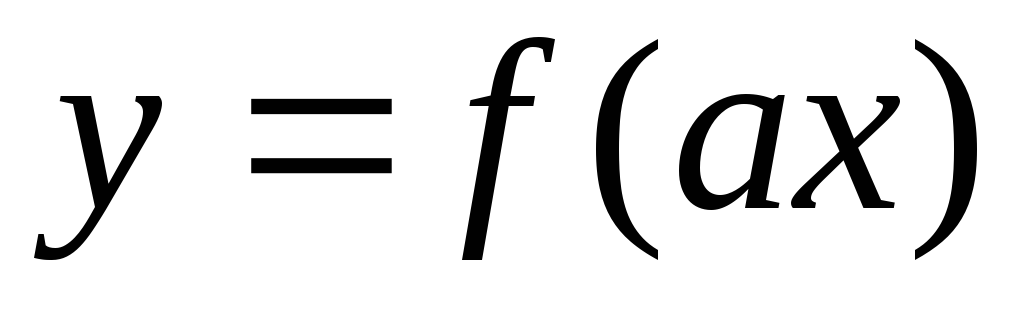получается из графика 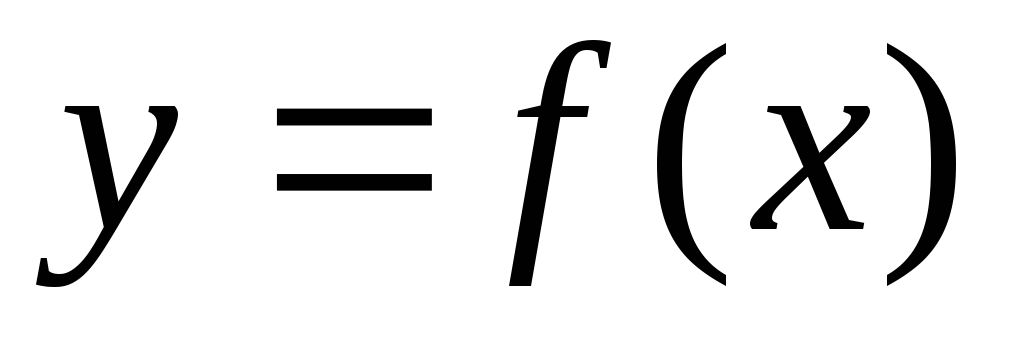сжатием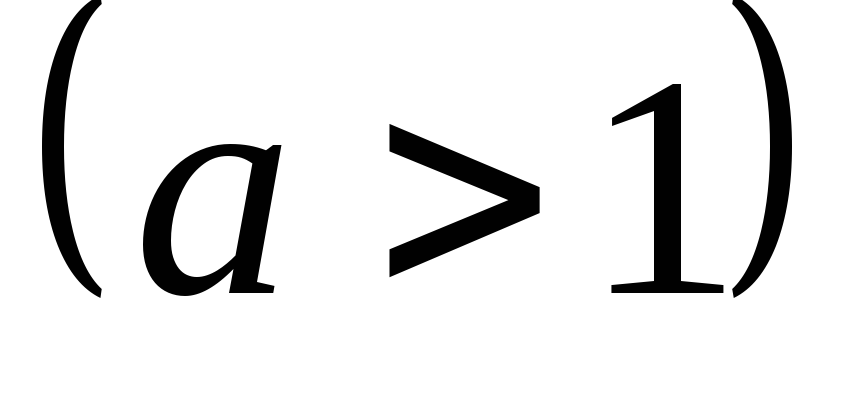или растяжением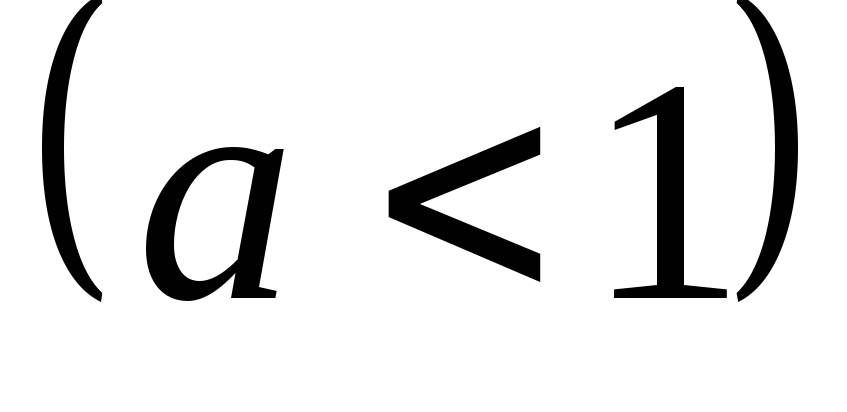его ва раз вдоль оси Ох. (т.е. к оси Оy).

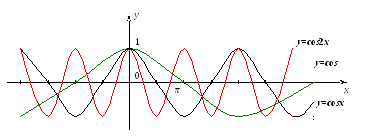
5. График функции y=f(x+b) получается из графика y=f(x) с помощью параллельного переноса (сдвига) его вдоль оси Ох влево (b>0) или вправо (b<0) на b единиц.

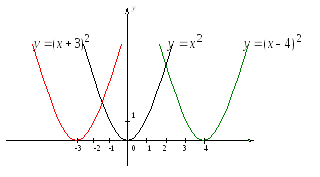
Построение графиков подобного рода в общем случае

сводится к проведению в соответствующем порядке операций 1-4.

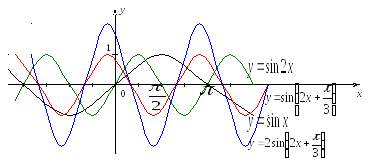
Пример. Построить график функции .

Решение.

1. Строим график ;

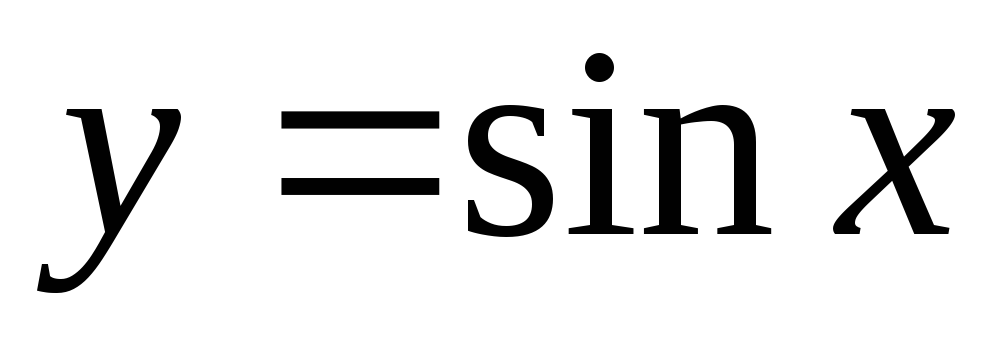2. сжимаем его вдоль осив 2 раза, получаем график;

3. сдвигаем график влево на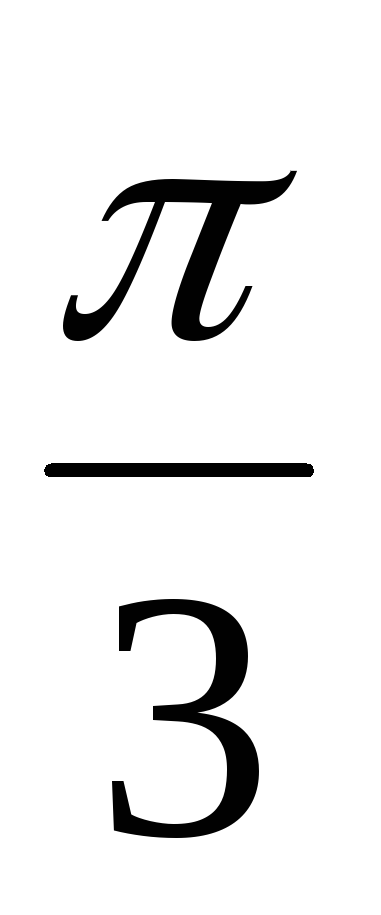и получаем график;

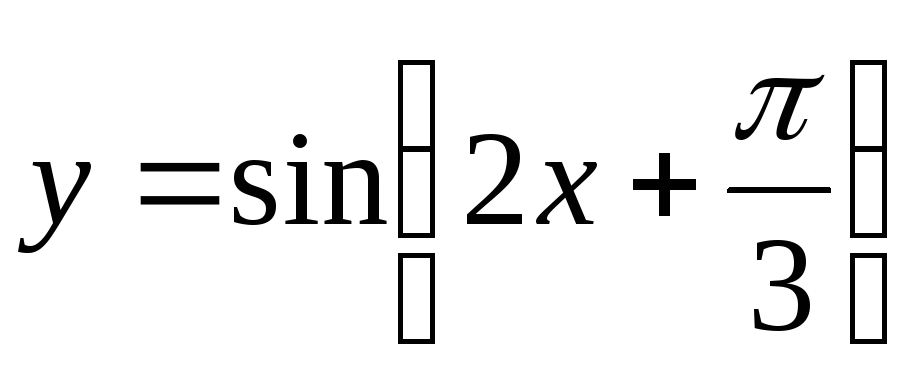4. растягиваем график 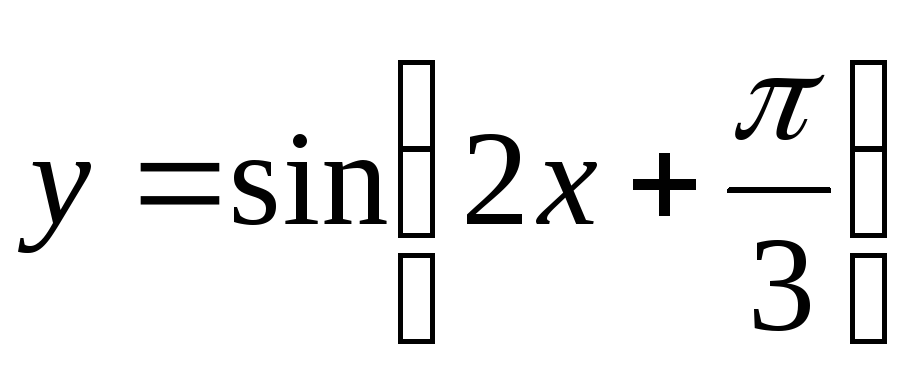вдоль оси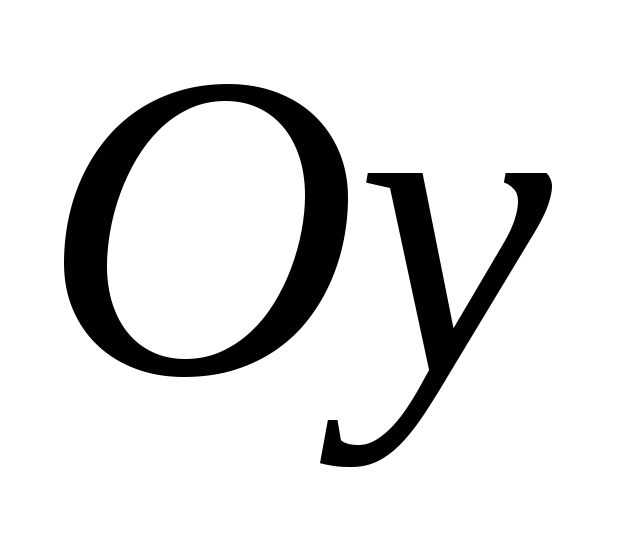в 2 раза и получаем требуемый график.

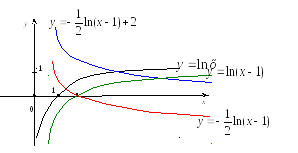
Пример. Построить график функции .

Решение.

1) строим график ;

2) сдвигаем его влево по осина 1, получаем график функции;

3) сжимаем график вдоль осив 2 раза и строим симметричный ему относительно оси, получаем график;

4) поднимаем график функции по оси Оy вверх на две единицы, получаем искомый график.

Задание 4.

Методом деформации и сдвигов построить график функции

№ зад № вар	1	2	3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30