3.3. Общая задача оптимизации

Общая задача оптимизации может быть сформулирована в виде:

(3.3.1)

где – выпуклое множество. В соответствии с теоремой Вейерштрасса, еслиявляется замкнутым ограниченным множеством, а функциянепрерывна на этом множестве, то она достигает насвоих максимального и минимального значений. Замкнутое ограниченное множество называется компактом. Если множествов (3.3.1) не является компактом, но функциясильно выпукла на, то в соответствии с теоремой Вейерштрасса и теоремой 3.2.3, функциядостигает насвоего минимального значения. Для решения задачи (3.3.1) важное значение имеют следующие теоремы.

Теорема 3.3.1

Если функция непрерывна и выпукла на выпуклом компакте, то множество решений

также выпукло.

Доказательство. Введем обозначение:

Требуется доказать, что . Поскольку функциявыпукла на,,выполнено неравенство

Правая часть этого неравенства равна , так как. Следовательно, в точкедостигается минимум функции, т.е. эта точка принадлежит множеству. Из полученного результата следует вывод о том, что множество решенийявляется выпуклым множеством. Теорема доказана.

Теорема 3.3.2

Если функция непрерывна и строго выпукла на выпуклом компакте, то множество решений

состоит из единственной точки , т.е.. Иначе говоря, строго выпуклая функция достигает минимума в единственной точке.

Доказательство. Доказательство проведем способом от противного. Допустим, что существуют точки . Поскольку строго выпуклая функция является выпуклой функцией, на нее распространяется доказанная выше теорема 3.3.1. В силу этого обстоятельства множество решенийявляется выпуклым. Тогда можно записать:

(3.3.2)

Так как функция строго выпукла на, справедливо неравенство

(3.3.3)

Используя обозначение , с учетом (3.3.2) для левой части неравенства (3.3.3) можно записать:

Поскольку , получаем, что правая часть неравенства (3.3.3) также равна. Таким образом, в отношении справедливости неравенства (3.3.3) имеет место противоречие. Следовательно, предположение о том, что множество решенийсостоит более чем из одной точки, является неверным. Теорема доказана.

Точка называется глобальным решением задачи (3.3.1), есливыполнено неравенство.

Точка называется локальным решением задачи (3.3.1), есливыполнено неравенство. Здесьявляется шаром радиусас центром в точке.

Напомним, что шаром радиуса с центром в точкеназывается множество точек, для которых выполнено неравенство:

Теорема 3.3.3

Пусть функция выпукла на выпуклом множестве. Тогда всякое локальное решение задачи (3.3.1) является глобальным.

Доказательство. Пусть точка является локальным решением задачи (3.3.1). Тогда, где– шар радиусас центром в точке. Выберем произвольно точкуи определим точкув виде, где. Поскольку множествовыпукло,. Из выражения дляследует:. Используя это соотношение, а также выражение для величины, получим:

(3.3.4)

Из (3.3.4) следует, что точка принадлежит шару(т.е. находится в окрестности точки) и с учетом ее принадлежности множествуможно записать:. Следовательно, выполнено неравенство

(3.3.5)

Учитывая выпуклость функции на множестве, запишем:

Из этого выражения и неравенства (3.3.5) следует:

а это означает, что точка является глобальным решением задачи (3.3.1). Теорема доказана.

Задачи оптимизации, в которых всякое локальное решение является глобальным, относят к так называемым унимодальным задачам и рассматривают в выпуклом программировании – разделе математического программирования, изучающем задачи минимизации, в которых минимизируемая функция выпукла, а ограничения заданы также выпуклыми функциями. Задачи такого типа встречаются в математической экономике, теории электрических цепей; к ним относятся также задачи аппроксимации функций.

Если задача оптимизации сформулирована в виде

(3.3.6)

то она представляет собой задачу безусловной оптимизации. В этом случае необходимым условием существования экстремума в точке является равенство нулю градиента функции в этой точке:(или).

Теорема 3.3.4

Пусть функция дифференцируема на выпуклом множествеи пусть точка– локальное решение задачи (3.3.1). Тогда справедливы следующие заключения:

1) выполнено неравенство;

2) если функция выпукла наи в точкевыполнено неравенство, то точкаявляется глобальным решением задачи (3.3.1).

Приведенные во 2-м пункте условия являются достаточными условиями существования глобального решения задачи (3.3.1).

Доказательство. 1). Поскольку точка является локальным решением задачи (3.3.1),при достаточно малыхвыполнено неравенство. Ясно, чтоимеемв силу выпуклости множества. Используя условие дифференцируемости функции, запишем:

После деления на (полагаем) полученное неравенство примет вид:

Поскольку при, неравенствобудет выполнено.

2). В соответствии с дифференциальным критерием выпуклости (3.2.3) и результатом, полученным в 1-м пункте теоремы, имеем:

т.е. – глобальное решение задачи (3.3.1). Теорема доказана.

Лемма 3.3.1

Пусть точка находится внутри множества, т.е., что означает, что имеется некоторая окрестность точки, целиком содержащаяся в множествевместе с точкой, и пусть для дифференцируемой нафункциивыполнено неравенство. Тогда.

Доказательство. В соответствии с условием леммы имеем, шар. Воспользуемся методом доказательства от противного. Предположим, что, тогда. Введем в рассмотрение точку, которую определим следующим образом:

(3.3.7)

Тогда для нормы из (3.3.7) получим:

откуда следует, что . Следовательно, точкадолжна удовлетворять неравенству, которое в соответствии с (3.3.7) может быть записано в виде:

Поскольку скалярное произведение в левой части этого неравенства равно , пришли к противоречию. Значит, предположение о том, что, было неверным. Таким образом,. Лемма доказана.

Лемма 3.3.2

Пусть множество является-мерным параллелепипедом, т.е.

(3.3.8)

и пусть на этом множестве заданы дифференцируемая функция и точка– локальное решение задачи (3.3.1). Тогда заключение, приведенное в п.1 теоремы 3.3.4, а именно:выполнено неравенство, эквивалентно следующему:

Доказательство. Прежде всего отметим, что множество , заданное в соответствии с (3.3.8), является выпуклым. Учитывая это обстоятельство, а также условия леммы, приходим к выводу, что в данном случае справедливо заключение теоремы 3.3.4, на которое указано в формулировке леммы. Поскольку

вышеупомянутое заключение теоремы 3.3.4 можно записать в виде: выполнено неравенство

(3.3.9)

Выделив из суммы в (3.3.9) -е слагаемое, получим:

(3.3.10)

Поскольку полученное неравенство должно выполняться , то оно должно иметь место и при. В этом случае (3.3.10) принимает вид:

(3.3.11)

Если выполнено условие , то выражениепринимает положительные, отрицательные значения, а также значение, равное нулю. Поэтому для выполнения неравенства (3.3.11) в любом из этих случаев необходимо и достаточно, чтобы значение производной в (3.3.11) было равно нулю:

Если , тои, следовательно, для выполнения (3.3.11) необходимо и достаточно, чтобы значение производной в (3.3.11) было неотрицательным, т.е. должно соблюдаться условие

Если , тои неравенство (3.3.11) будет выполнено тогда и только тогда, когда будет иметь место соотношение

Лемма доказана.

Следствие. Если множество в условии леммы 3.3.2 представляет собой неотрицательный ортант пространства, т.е.

,

то в этом случае из доказанной леммы следует, что заключение «выполнено неравенство » эквивалентно следующему:

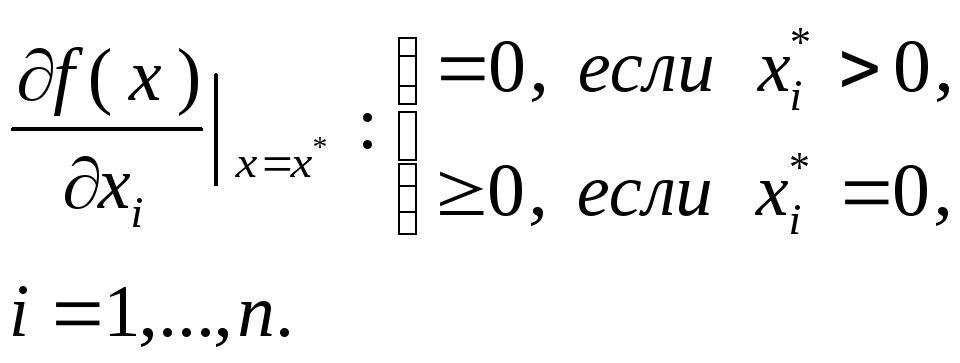
Пример 3.3.1

Анализ условия задачи показывает, что множество является выпуклым, а функцияможет быть представлена в виде:, где

–симметрическая положительно определенная матрица, . Следовательно, в соответствии с замечаниями к формуле (3.2.7), функцияявляется сильно выпуклой на. На основании изложенного в начале данного раздела и теоремы 3.3.2 (с учетом того, что сильно выпуклая функция является также строго выпуклой) приходим к заключению о том, что в рассматриваемой задаче функциядостигает минимума в единственной точке.

В соответствии с леммой 3.3.2 находим:

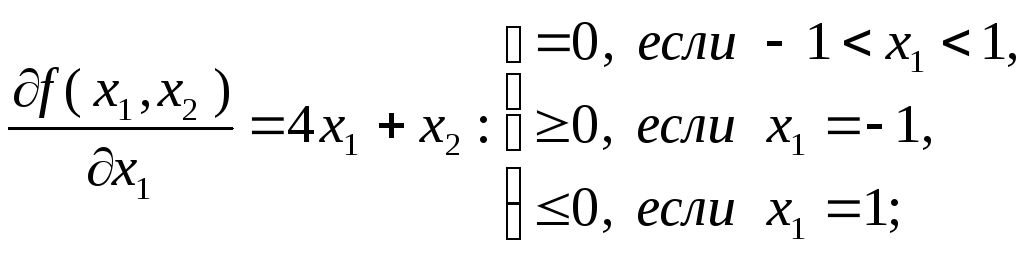(3.3.12)

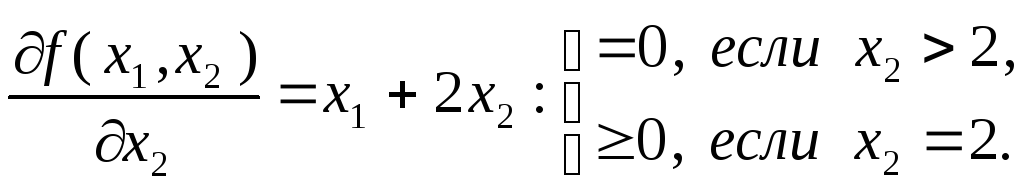(3.3.13)

Комбинируя варианты образования соотношений для частных производных, представленные в (3.3.12) и (3.3.13), по одному из каждой группы, получаем шесть систем, из которых лишь одна окажется совместной в силу существования минимума в единственной точке:

1)

2)

3)

4)

5)

6)

Решая первую систему, получаем:

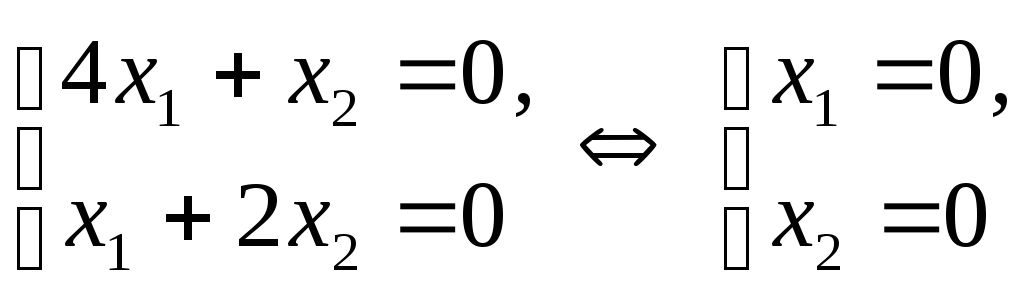–не удовлетворяет условию . Следовательно, первая система несовместна.

Рассмотрим вторую систему:

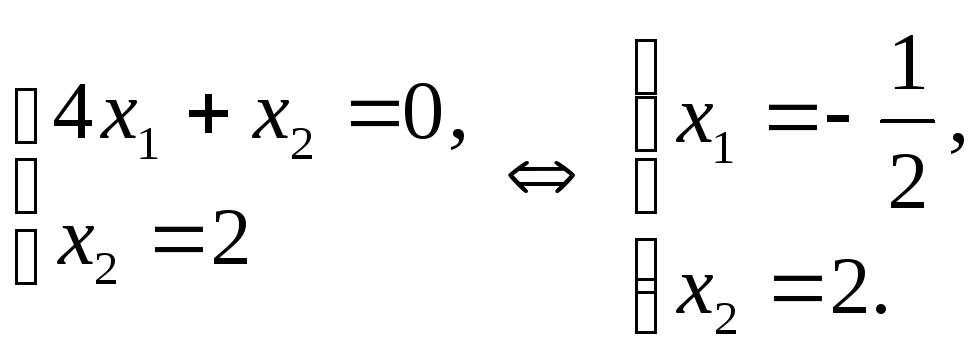
Найденное решение системы уравнений удовлетворяет неравенствам второй системы. Следовательно, точка есть решение задачи. Все оставшиеся нерассмотренными системы несовместны.