
- •Линейная алгебра и геометрия.
- •1.Определители и их свойства.
- •2.Миноры и алгебраические дополнения. Теорема о разложении опред. По элементам строки или столбца.
- •3.Системы трех линейных уравнений с тремя неизвестными, правило Крамера.
- •4. Матрицы, действия над матрицами.
- •5. Теорема о ложном разложении опред. Вычисление произвед. Квадратной матрицы на ее присоединенную.
- •6.Обратная матрица. Матричный способ решения систем линейных уравнений.
- •7.Векторы. Сложение векторов и умножение их на число.
- •10.Система координат. Выражение координат вектора через координаты его конца и начала.
- •11. Деление отрезка в данном отношении.
- •12.Прямоугольная система координат. Длина вектора. Расстояние между двумя точками.
- •14.Скалярное произведение и его свойства.
- •16.Векторное произведение и его свойства. Геометрический смысл модуля.
- •17.Вычисление координат векторного произведения. Применение к вычислению площадей.
- •18 Смешанное произведение векторов и его геометрический смысл.
- •19 Вычисление смешанного произведения в координатах. Признак компланарности трех векторов
- •20. Уравнение прямой на плоскости, проходящей через данную точку перпендикулярно данному вектору.
- •21. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.
- •22. Уравнение плоскости, проходящей через данную точку параллельно двум данным векторам.
- •23. Уравнение плоскости проходящей через три данные точки.
- •24. Условие параллельности вектора и плоскости. Неполные уравнения плоскости.
- •25.Расстояние от точки до плоскости
- •26. Угол между двумя прямыми на плоскости. Условия параллельности и перпендикулярности прямых.
- •28.Уравнение прямой, проходящей через данную точку параллельно данному вектору. Угол между прямыми.
- •29. Приведение общих уравнений прямой в пространстве к каноническому виду.
- •30.Эллипс: геометрическое определение, вывод и исследование канонического уравнения
- •32.Парабола: геометрическое определение, вывод и исследование канонического уравнения
- •Дифференциальное исчисление.
- •1.Определение предела функции. Бесконечно малые. Представление функции в виде суммы константы и бесконечно малой.
- •2.Свойства бесконечно малых.
- •3. Предел суммы, произведения и частного.
- •4. Предел функции на бесконечности. Предел числовой последовательности.
- •5. Теорема о «двух милиционерах».
- •6. Первый замечательный предел.
- •7.Теорема о пределе монотонной ограниченной функции. Второй замечательный предел.
- •8. Сравнение бесконечно малых. Эквивалентные бесконечно малые.
- •9. Таблица эквивалентных бесконечно малых.
- •10.Непрерывность функции в точке. Односторонние пределы. Классификация точек разрыва.
- •13. Определение производной и ее геометрический смысл. Уравнение касательной и нормали к графику функции в данной точке.
- •14. Доказать, что дифференцируемая функция непрерывна.
- •15.Производная суммы и произведения функций.
- •17.Производная сложной функции.
- •20.Дифференциал функции: определение и формула для вычисления. Эквивалентность дифференцируемости и существования производной.
- •21.Теорема Ферма и Ролля.
- •23.Теорема коши об отношении приращений двух функций на отрезке
- •24.Правила Лопиталя
- •26.Возрастание и убывание функции. Доказать что, при положительной производной функция возрастает.
- •27.Точки экстремума,достаточное условие экстремума для первой производной.
- •28.Точки экстремума. Достаточное условие экстремума по второй производной.
- •29.Выпуклость и вогнутость ,точки перегиба связь со второй производной
- •31.Частные производные. Независимость смешанных частных производных от порядка дифференцирования.
- •32.Дифференцируемость функций нескольких переменных. Дифференциал функций.
- •33.Частные производные сложной функции.
- •34.Неявные функции и их производные.
- •35.Экстремумы функций двух переменных. Необходимое условие экстремума.
- •36.Достаточные условия экстремума функции двух переменных.
26. Угол между двумя прямыми на плоскости. Условия параллельности и перпендикулярности прямых.
Угломмежду прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.
Пусть в пространстве заданы две прямые:

Очевидно, что
за угол φ между прямыми можно принять
угол между их направляющими векторами
 и
и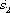 .
Так как
.
Так как ,
то по формуле для косинуса угла между
векторами получим
,
то по формуле для косинуса угла между
векторами получим
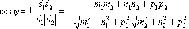 .
.
Условия
параллельности и перпендикулярности
двух прямых равносильны условиям
параллельности и перпендикулярности
их направляющих векторов S1 и
 :
:
Две прямые
параллельны тогда и только тогда,
когда их соответствующие коэффициенты
пропорциональны, т.е.l1параллельнаl2тогда и только
тогда, когда s1 параллелен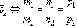 .
.
Две прямые
перпендикулярнытогда и только
тогда, когда сумма произведений
соответствующих коэффициентов равна
нулю: .
.
Условия параллельности и перпендикулярности прямых.
Если
прямые
 и
и параллельны,
то угол
параллельны,
то угол
 и
и ,
откуда из формулы угла между двумя
прямыми
,
откуда из формулы угла между двумя
прямыми
 .
И наоборот, если
.
И наоборот, если ,
то по этой же формуле
,
то по этой же формуле и
и .
.
Т.о., равенство угловых коэффициентов является необходимым и достаточным условием параллельности 2х прямых.
 -
условие
параллельности двух прямых.
-
условие
параллельности двух прямых.
Если
прямые перпендикулярны,
то
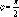 ,
при этом
,
при этом или
или ,
откуда
,
откуда или
или .
.
Справедливо так же и обратное утверждение.
Т.о., для перпендикулярности прямых необходимо и достаточно, чтобы их угловые коэффициенты были обратны по величине и противоположны по знаку.
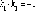 -
условие
перпендикулярности двух прямых.
-
условие
перпендикулярности двух прямых.
Если
две прямые заданы уравнениями в общем
виде:
 и
и ,
то учитывая
их угловые коэффициенты
,
то учитывая
их угловые коэффициенты
 и
и ,
условие параллельности прямых имеет
вид:
,
условие параллельности прямых имеет
вид: .
.
Следовательно, условием параллельности прямых, заданных общими уравнениями является пропорциональность коэффициентов при переменных.
Условие
перпендикулярности прямых
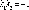 в
этом случае примет вид
в
этом случае примет вид или
или ,
,
Т.е. условием перпендикулярности двух прямых, заданных общими уравнениями, является равенство нулю суммы произведений коэффициентов при переменных х и у.
27. Угол между двумя плоскостями. Условия параллельности и перпендикулярности прямых.
Рассмотрим две плоскости α1и α2, заданные соответственно уравнениями:

Под угломмежду
двумя плоскостями будем понимать один
из двугранных углов, образованных этими
плоскостями. Очевидно, что угол между
нормальными векторами и
и плоскостей
α1и α2равен одному из
указанных смежных двугранных углов
плоскостей
α1и α2равен одному из
указанных смежных двугранных углов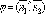 или
или .
Поэтому
.
Поэтому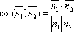 .
Т.к.
.
Т.к. и
и ,
то
,
то
 .
.
Пример.Определить угол между плоскостямиx+2y-3z+4=0 и 2x+3y+z+8=0.

Условие параллельности двух плоскостей.
Две плоскости α1и α2параллельны тогда и только
тогда, когда их нормальные векторы и
и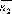 параллельны,
а значит
параллельны,
а значит .
.
Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:
 или
или
Условие перпендикулярности плоскостей.
Ясно, что две плоскости
перпендикулярны тогда и только тогда,
когда их нормальные векторы перпендикулярны,
а следовательно,
 или
или .
.
Таким образом,
 .
.
28.Уравнение прямой, проходящей через данную точку параллельно данному вектору. Угол между прямыми.
Каждый не равный нулю вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором этой прямой.
Направляющий вектор
произвольной прямой в дальнейшем
обозначается буквой
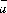 ,
его координаты - буквами l, m, n:
,
его координаты - буквами l, m, n:
 .
.
Если известна одна точка
 прямой
и направляющий вектор
прямой
и направляющий вектор ,
то прямая может быть определена (двумя)
уравнениями вида
,
то прямая может быть определена (двумя)
уравнениями вида
 .
(1)
.
(1)
В таком виде уравнения прямой называются каноническими.
Канонические уравнения
прямой, проходящей через данные точки
 и
и имеют
вид
имеют
вид
 .
(2)
.
(2)
Обознчим буквой t каждое из равных отношений в канонических уравнениях (1); получим
 .
.
Отсюда
 ,
, ,
, .
(3)
.
(3)
Это - параметрические
уравнения прямой, проходящей через
точку
 в
направлении вектора
в
направлении вектора .
В уравнениях (3) t рассматривается как
произвольно изменяющийся параметр, x,
y, z - как функции от t; при изменении t
величины x, y, z меняются так, что точка
M(x; y; z) движется по данной прямой.
.
В уравнениях (3) t рассматривается как
произвольно изменяющийся параметр, x,
y, z - как функции от t; при изменении t
величины x, y, z меняются так, что точка
M(x; y; z) движется по данной прямой.
Если параметр t
рассматривать как переменное время, а
уравнения (3) как уравнения движения
точки М, то эти уравнения будут определять
прямолинейное и равномерное движение
точки М. При t=0 точка М совпадает с точкой
 .
Скорость v точки М постоянная и определяется
формулой
.
Скорость v точки М постоянная и определяется
формулой
 .
.
Пусть
прямые
 и
и заданы
общими уравнениями
заданы
общими уравнениями
|
|
Обозначим
через φ величину угла между прямыми
 и
и (напомним,
что угол между прямыми измеряется от
0° до 90°), а через ψ – угол между нормальными
векторами
(напомним,
что угол между прямыми измеряется от
0° до 90°), а через ψ – угол между нормальными
векторами и
и этих
прямых. Если ψ ≤ 90°, то φ = ψ.
Если же ψ > 90°, то φ = 180° – ψ.
В обоих случаях верно равенство
этих
прямых. Если ψ ≤ 90°, то φ = ψ.
Если же ψ > 90°, то φ = 180° – ψ.
В обоих случаях верно равенство следует,
что
следует,
что
|
|
и, следовательно,
|
|
Записав через координаты, получим
|
|
Если
прямые
 и
и заданы
уравнениями с угловыми коэффициентами
заданы
уравнениями с угловыми коэффициентами и
и
|
|
то
нормальные векторы этих прямых могут
быть
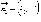
 и
выражение для косинуса угла между этими
прямыми будет иметь вид:
и
выражение для косинуса угла между этими
прямыми будет иметь вид:
|
|

 и
и


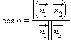

 и
и

