
- •Линейная алгебра и геометрия.
- •1.Определители и их свойства.
- •2.Миноры и алгебраические дополнения. Теорема о разложении опред. По элементам строки или столбца.
- •3.Системы трех линейных уравнений с тремя неизвестными, правило Крамера.
- •4. Матрицы, действия над матрицами.
- •5. Теорема о ложном разложении опред. Вычисление произвед. Квадратной матрицы на ее присоединенную.
- •6.Обратная матрица. Матричный способ решения систем линейных уравнений.
- •7.Векторы. Сложение векторов и умножение их на число.
- •10.Система координат. Выражение координат вектора через координаты его конца и начала.
- •11. Деление отрезка в данном отношении.
- •12.Прямоугольная система координат. Длина вектора. Расстояние между двумя точками.
- •14.Скалярное произведение и его свойства.
- •16.Векторное произведение и его свойства. Геометрический смысл модуля.
- •17.Вычисление координат векторного произведения. Применение к вычислению площадей.
- •18 Смешанное произведение векторов и его геометрический смысл.
- •19 Вычисление смешанного произведения в координатах. Признак компланарности трех векторов
- •20. Уравнение прямой на плоскости, проходящей через данную точку перпендикулярно данному вектору.
- •21. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.
- •22. Уравнение плоскости, проходящей через данную точку параллельно двум данным векторам.
- •23. Уравнение плоскости проходящей через три данные точки.
- •24. Условие параллельности вектора и плоскости. Неполные уравнения плоскости.
- •25.Расстояние от точки до плоскости
- •26. Угол между двумя прямыми на плоскости. Условия параллельности и перпендикулярности прямых.
- •28.Уравнение прямой, проходящей через данную точку параллельно данному вектору. Угол между прямыми.
- •29. Приведение общих уравнений прямой в пространстве к каноническому виду.
- •30.Эллипс: геометрическое определение, вывод и исследование канонического уравнения
- •32.Парабола: геометрическое определение, вывод и исследование канонического уравнения
- •Дифференциальное исчисление.
- •1.Определение предела функции. Бесконечно малые. Представление функции в виде суммы константы и бесконечно малой.
- •2.Свойства бесконечно малых.
- •3. Предел суммы, произведения и частного.
- •4. Предел функции на бесконечности. Предел числовой последовательности.
- •5. Теорема о «двух милиционерах».
- •6. Первый замечательный предел.
- •7.Теорема о пределе монотонной ограниченной функции. Второй замечательный предел.
- •8. Сравнение бесконечно малых. Эквивалентные бесконечно малые.
- •9. Таблица эквивалентных бесконечно малых.
- •10.Непрерывность функции в точке. Односторонние пределы. Классификация точек разрыва.
- •13. Определение производной и ее геометрический смысл. Уравнение касательной и нормали к графику функции в данной точке.
- •14. Доказать, что дифференцируемая функция непрерывна.
- •15.Производная суммы и произведения функций.
- •17.Производная сложной функции.
- •20.Дифференциал функции: определение и формула для вычисления. Эквивалентность дифференцируемости и существования производной.
- •21.Теорема Ферма и Ролля.
- •23.Теорема коши об отношении приращений двух функций на отрезке
- •24.Правила Лопиталя
- •26.Возрастание и убывание функции. Доказать что, при положительной производной функция возрастает.
- •27.Точки экстремума,достаточное условие экстремума для первой производной.
- •28.Точки экстремума. Достаточное условие экстремума по второй производной.
- •29.Выпуклость и вогнутость ,точки перегиба связь со второй производной
- •31.Частные производные. Независимость смешанных частных производных от порядка дифференцирования.
- •32.Дифференцируемость функций нескольких переменных. Дифференциал функций.
- •33.Частные производные сложной функции.
- •34.Неявные функции и их производные.
- •35.Экстремумы функций двух переменных. Необходимое условие экстремума.
- •36.Достаточные условия экстремума функции двух переменных.
18 Смешанное произведение векторов и его геометрический смысл.
Тройкой векторов
называются три вектора, если указано,
какой из них считается первым, какой
вторым и какой третьим. Тройку векторов
записывают в порядке нумерации; например,
запись
 ,
, ,
, означает,
что вектор
означает,
что вектор считается
первым,
считается
первым, -
вторым,
-
вторым, -
третьим.
-
третьим.
Тройка некомпланарных
векторов
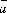 ,
, ,
, называется
правой, если составляющие ее векторы,
будучи приведены к общему началу,
располагаются в порядке нумерации
аналогично тому, как расположены большой,
указательный и средний пальцы правой
руки. Если векторы
называется
правой, если составляющие ее векторы,
будучи приведены к общему началу,
располагаются в порядке нумерации
аналогично тому, как расположены большой,
указательный и средний пальцы правой
руки. Если векторы ,
,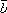 ,
, расположены
аналогично тому, как расположены большой,
указательный и средний пальцы левой
руки, то тройка этих векторов называется
левой.
расположены
аналогично тому, как расположены большой,
указательный и средний пальцы левой
руки, то тройка этих векторов называется
левой.
Смешанным произведенем
трех векторов
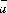 ,
, ,
, называется
число, равное векторному произведению
называется
число, равное векторному произведению ,
умноженному скалярно на вектор
,
умноженному скалярно на вектор ,
то есть
,
то есть .
.
Имеет место тождество ,
ввиду чего для обозначения смешанного
произведения
,
ввиду чего для обозначения смешанного
произведения употребляется
более простой символ
употребляется
более простой символ .
Таким образом,
.
Таким образом,
 ,
, .
.
Смешанное произведение
 равно
объему параллелепипеда, построенного
на векторах
равно
объему параллелепипеда, построенного
на векторах ,
, ,
, ,
взятого со знаком плюс, если тройка
,
взятого со знаком плюс, если тройка правая,
и со знаком минус, если эта тройка левая.
Если векторы
правая,
и со знаком минус, если эта тройка левая.
Если векторы ,
, ,
,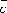 компланарны
(и только в этом случае), смешанное
произведение
компланарны
(и только в этом случае), смешанное
произведение равно
нулю; иначе говоря, равенство
равно
нулю; иначе говоря, равенство

есть необходимое и
достаточное условие компланарности
векторов
 ,
,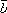 ,
, .
.
Применение смешанного произведения
Применяется для вычисления объемов.
Геометрический
смысл
смешанного произведения. Смешанное
произведение 3-х векторов с точностью
до знака равно объёму параллелепипеда,
построенного на этих векторах, как на
рёбрах, т.е.
 .
.
Таким
образом,
 и
и .
.
Доказательство.
Отложим векторы
 от
общего начала и построим на них
параллелепипед. Обозначим
от
общего начала и построим на них
параллелепипед. Обозначим и
заметим, что
и
заметим, что .
По определению скалярного произведения
.
По определению скалярного произведения
 .
Предполагая, что
.
Предполагая, что
 и
обозначив черезh
высоту параллелепипеда, находим
и
обозначив черезh
высоту параллелепипеда, находим
 .
.
Таким
образом, при

Если
же
 ,
то
,
то и
и .
Следовательно,
.
Следовательно,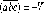 .
.
Объединяя
оба эти случая, получаем
 или
или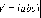 .
.
Из
доказательства этого свойства в частности
следует, что если тройка векторов
 правая,
то смешанное произведение
правая,
то смешанное произведение ,
а если
,
а если –
левая, то
–
левая, то .
.
Для
любых векторов
 ,
, ,
, справедливо
равенство
справедливо
равенство
 .
.
Доказательство
этого свойства следует из свойства 1.
Действительно, легко показать, что
 и
и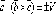 .
Причём знаки "+" и "–" берутся
одновременно, т.к. углы между векторами
.
Причём знаки "+" и "–" берутся
одновременно, т.к. углы между векторами и
и и
и и
и одновременно
острые или тупые.
одновременно
острые или тупые.
При перестановке любых двух сомножителей смешанное произведение меняет знак.
Действительно,
если рассмотрим смешанное произведение
 ,
то, например,
,
то, например, или
или
 .
.
19 Вычисление смешанного произведения в координатах. Признак компланарности трех векторов
Если векторы
 ,
, ,
,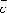 заданы
своими координатами:
заданы
своими координатами:
,

 ,
,
то смешанное произведение
 определяется
формулой
определяется
формулой
 .
.
Напомним, что система
координатных осей предполагается правой
(вместе с тем является правой и тройка
векторов
 ,
, ,
, ).
).
Свойства смешанного произведения.
1 Кососимметричность. При перестановке любых двух векторов смешанное произведение меняет знак:


Полилинейность, т.е. линейность по каждому сомножителю:
2 

3
 ,
,

Эти свойства следуют из соответствующих свойств определителя, так как смешанное произведение в координатах выражается в виде определителя.
Смешанное
произведение
 тогда
и только тогда, когда один из сомножителей
равен нулю или векторы
тогда
и только тогда, когда один из сомножителей
равен нулю или векторы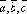 –
компланарны.
–
компланарны.
Доказательство.
Предположим, что
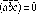 ,
т.е.
,
т.е. ,
тогда
,
тогда или
или или
или .
.
Если
 ,
то
,
то или
или или
или .
Поэтому
.
Поэтому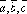 –
компланарны.
–
компланарны.
Если
 ,
то
,
то ,
, ,
, -
компланарны.
-
компланарны.
Пусть векторы
 –
компланарны и α – плоскость, которой
они параллельны , т. е.
–
компланарны и α – плоскость, которой
они параллельны , т. е. и
и .
Тогда
.
Тогда ,
а значит
,
а значит ,
поэтому
,
поэтому или
или .
.
Т.о.,
необходимым и достаточным условием
компланарности 3-х векторов является
равенство нулю их смешанного произведения.
Кроме того, отсюда следует, что три
вектора
 образуют
базис в пространстве, если
образуют
базис в пространстве, если .
.
Если
векторы заданы в координатной форме
 ,
то можно показать, что их смешанное
произведение находится по формуле:
,
то можно показать, что их смешанное
произведение находится по формуле:
 .
.
Т.
о., смешанное произведение
 равно
определителю третьего порядка, у которого
в первой строке стоят координаты первого
вектора, во второй строке – координаты
второго вектора и в третьей строке –
третьего вектора.
равно
определителю третьего порядка, у которого
в первой строке стоят координаты первого
вектора, во второй строке – координаты
второго вектора и в третьей строке –
третьего вектора.
