- •Линейная алгебра и геометрия.
- •1.Определители и их свойства.
- •2.Миноры и алгебраические дополнения. Теорема о разложении опред. По элементам строки или столбца.
- •3.Системы трех линейных уравнений с тремя неизвестными, правило Крамера.
- •4. Матрицы, действия над матрицами.
- •5. Теорема о ложном разложении опред. Вычисление произвед. Квадратной матрицы на ее присоединенную.
- •6.Обратная матрица. Матричный способ решения систем линейных уравнений.
- •7.Векторы. Сложение векторов и умножение их на число.
- •10.Система координат. Выражение координат вектора через координаты его конца и начала.
- •11. Деление отрезка в данном отношении.
- •12.Прямоугольная система координат. Длина вектора. Расстояние между двумя точками.
- •14.Скалярное произведение и его свойства.
- •16.Векторное произведение и его свойства. Геометрический смысл модуля.
- •17.Вычисление координат векторного произведения. Применение к вычислению площадей.
- •18 Смешанное произведение векторов и его геометрический смысл.
- •19 Вычисление смешанного произведения в координатах. Признак компланарности трех векторов
- •20. Уравнение прямой на плоскости, проходящей через данную точку перпендикулярно данному вектору.
- •21. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.
- •22. Уравнение плоскости, проходящей через данную точку параллельно двум данным векторам.
- •23. Уравнение плоскости проходящей через три данные точки.
- •24. Условие параллельности вектора и плоскости. Неполные уравнения плоскости.
- •25.Расстояние от точки до плоскости
- •26. Угол между двумя прямыми на плоскости. Условия параллельности и перпендикулярности прямых.
- •28.Уравнение прямой, проходящей через данную точку параллельно данному вектору. Угол между прямыми.
- •29. Приведение общих уравнений прямой в пространстве к каноническому виду.
- •30.Эллипс: геометрическое определение, вывод и исследование канонического уравнения
- •32.Парабола: геометрическое определение, вывод и исследование канонического уравнения
- •Дифференциальное исчисление.
- •1.Определение предела функции. Бесконечно малые. Представление функции в виде суммы константы и бесконечно малой.
- •2.Свойства бесконечно малых.
- •3. Предел суммы, произведения и частного.
- •4. Предел функции на бесконечности. Предел числовой последовательности.
- •5. Теорема о «двух милиционерах».
- •6. Первый замечательный предел.
- •7.Теорема о пределе монотонной ограниченной функции. Второй замечательный предел.
- •8. Сравнение бесконечно малых. Эквивалентные бесконечно малые.
- •9. Таблица эквивалентных бесконечно малых.
- •10.Непрерывность функции в точке. Односторонние пределы. Классификация точек разрыва.
- •13. Определение производной и ее геометрический смысл. Уравнение касательной и нормали к графику функции в данной точке.
- •14. Доказать, что дифференцируемая функция непрерывна.
- •15.Производная суммы и произведения функций.
- •17.Производная сложной функции.
- •20.Дифференциал функции: определение и формула для вычисления. Эквивалентность дифференцируемости и существования производной.
- •21.Теорема Ферма и Ролля.
- •23.Теорема коши об отношении приращений двух функций на отрезке
- •24.Правила Лопиталя
- •26.Возрастание и убывание функции. Доказать что, при положительной производной функция возрастает.
- •27.Точки экстремума,достаточное условие экстремума для первой производной.
- •28.Точки экстремума. Достаточное условие экстремума по второй производной.
- •29.Выпуклость и вогнутость ,точки перегиба связь со второй производной
- •31.Частные производные. Независимость смешанных частных производных от порядка дифференцирования.
- •32.Дифференцируемость функций нескольких переменных. Дифференциал функций.
- •33.Частные производные сложной функции.
- •34.Неявные функции и их производные.
- •35.Экстремумы функций двух переменных. Необходимое условие экстремума.
- •36.Достаточные условия экстремума функции двух переменных.
14.Скалярное произведение и его свойства.
Опр.
Скалярным произведением векторов 
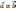 наз. число (
наз. число (
 ),
равное произведению длин этих векторов
и косинуса угла φ=< (
),
равное произведению длин этих векторов
и косинуса угла φ=< (
 )
между ними
)
между ними
(
 )=
|
)=
|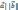
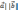 cosφ.
Скалярное произведение векторов равно
произведению длины одного вектора на
величину проекции другого вектора на
направление первого вектора: (
cosφ.
Скалярное произведение векторов равно
произведению длины одного вектора на
величину проекции другого вектора на
направление первого вектора: (
 )=
|
)=
|
 =
=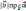
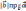
Из
определения следует, что (
 )=0,
если либо
)=0,
если либо
 =0,
либоcosφ=0,
т.е.
=0,
либоcosφ=0,
т.е. 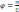
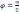 ;
т.е.
;
т.е.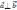
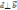 .⇒для
ненулевых векторов : (
.⇒для
ненулевых векторов : (
 )=0⇔
)=0⇔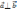
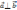 .
.
Скалярный
квадрат вектора, т.е. скалярное произведение
вектора на себя, равен квадрату его
модуля: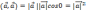
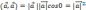
Свойства скалярного произведения .
(

 )=(
)=(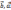
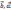 )-свойство
симметричности
)-свойство
симметричности(λ

 )=λ(
)=λ(
 )
(2,3)-линейность скалярного
произведения по первому сомножителю.
)
(2,3)-линейность скалярного
произведения по первому сомножителю.(
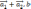
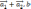 )=(
)=(
 )+(
)+(
 )
)
15.вычисление скалярного произведения через координаты сомножителей. Вычисление угла между векторами.
Если

 =(
=(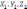
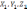 ),
),
 =
=
 ),
то (
),
то (
 )=
)=
 ,
т.е. скалярное произведение двух векторов
равно сумме попарных произведений
соответствующих координат.
,
т.е. скалярное произведение двух векторов
равно сумме попарных произведений
соответствующих координат.
Применение.
Основное применение скалярного
произведения состоит в вычислении углов
между векторами: cosφ=
 =
=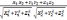
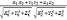 .
отсюда получаем условие перпендикулярности
двух векторов:
.
отсюда получаем условие перпендикулярности
двух векторов: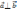
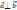 ⇔
⇔
 )=0⇔
)=0⇔
 =0.
=0.
Кроме
того,с помощью скалярного произведения
можно найти величину проекции одного
вектора на другой вектор(на ось,
определяемую другим вектором): 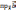
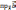 =
=

16.Векторное произведение и его свойства. Геометрический смысл модуля.
Опр.
Векторным произведением вектора 
 на вектор
на вектор
 наз. вектор
наз. вектор
 ,
который обозначается [
,
который обозначается [
 ]
и определяется условиями:
1) его длина
равна произведению длин этих векторов
и синус угла φ=<
]
и определяется условиями:
1) его длина
равна произведению длин этих векторов
и синус угла φ=<
 )
между ними:
)
между ними: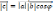
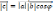 ;
;
2)
его направление характеризуется тем,
что: а)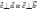
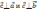 ;
б) векторы
;
б) векторы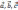
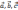 образуют правую тройку. Это значит, что
если отложить эти векторы от одной точки
и смотреть из конца третьего вектора
образуют правую тройку. Это значит, что
если отложить эти векторы от одной точки
и смотреть из конца третьего вектора
 , то кратчайший поворот от первого
вектора
, то кратчайший поворот от первого
вектора
 ко второму
ко второму
 будет осуществляться против часовой
стрелки.
будет осуществляться против часовой
стрелки.
(в физике-правило буравчика).
Пример.
[I,j]=
 .|[
.|[
 ]|=|
]|=|
 ||
||
 |sin
|sin
 =1.
По опр. |
=1.
По опр. |
 |=1,
|=1,
 ⏊
⏊
 ,
,

 ⏊
⏊
 и векторы
и векторы 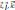
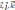 образуют правую тройку. Видно , что
векторы .[
образуют правую тройку. Видно , что
векторы .[
 ]
и
]
и
 имеют одинаковую длину и направление⇒совпадают.
имеют одинаковую длину и направление⇒совпадают.
Если

 ,
то <
,
то <
 )=0
либо <
)=0
либо <
 )=П⇒
[
)=П⇒
[
 ]=0.
В частности, для любого вектора
]=0.
В частности, для любого вектора
 имеем [
имеем [
 ]=0.
]=0.
Из
геометрии известно, что площадь
параллелограмма равна произведению
длин его сторон на синус угла между
ними.⇒
геометрический смысл модуля векторного
произведения: длина векторного
произведения двух векторов равна площади
параллелограмма, построенного на этих
векторах, т.е. |[
 ]|=|
]|=|
 ||
||
 |sinφ=
|sinφ=
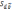 .
.
Свойства :
[

 ]=-[
]=-[
 ]-свойство
кососимметричности
]-свойство
кососимметричности[λ

 ]=λ[
]=λ[
 ]
]
[

 ]=[
]=[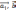
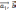 ]+[
]+[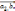
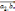 ]-(2,3)-
линейность векторного произведения
по первому сомножителю
]-(2,3)-
линейность векторного произведения
по первому сомножителю
17.Вычисление координат векторного произведения. Применение к вычислению площадей.
Векторным произведениемвектора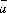 на
вектор
на
вектор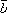 называется
вектор, обозначаемый символом
называется
вектор, обозначаемый символом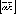 и
определяемый следующими тремя условиями:
и
определяемый следующими тремя условиями:
1). Модуль вектора
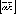 равен
равен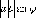 ,
где
,
где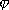 -
угол между векторами
-
угол между векторами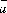 и
и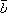 ;
;
2). Вектор
 перпендикулярен
к каждому из вектора
перпендикулярен
к каждому из вектора и
и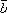 ;
;
3). Направление вектора
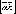 соответствует
«правилу правой руки». Это означает,
что если векторы
соответствует
«правилу правой руки». Это означает,
что если векторы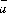 ,
,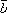 и
и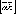 приведены
к общему началу, то вектор
приведены
к общему началу, то вектор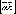 должен
быть направлен так, как направлен средний
палец правой руки, большой палец которой
направлен по первому сомножителю (то
есть по вектору
должен
быть направлен так, как направлен средний
палец правой руки, большой палец которой
направлен по первому сомножителю (то
есть по вектору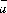 ),
а указательный - по второму (то есть по
вектору
),
а указательный - по второму (то есть по
вектору ).
).
Векторное произведение зависит от порядка сомножителей. Свойства векторного произведения.
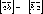 .
.
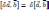
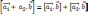
Модуль векторного произведения
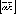 равен
площади S параллелограмма, построенного
на векторах
равен
площади S параллелограмма, построенного
на векторах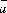 и
и :
:
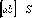 .
.
Само векторное произведение может быть выражено формулой
 ,
,
где
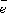 -
орт векторного произведения.
-
орт векторного произведения.
Векторное произведение
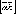 обращается
в нуль тогда и только тогда, когда векторы
обращается
в нуль тогда и только тогда, когда векторы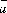 и
и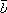 компланарны.
В частности,
компланарны.
В частности,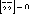 .
.
Если система координатных осей правая
и векторы
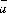 и
и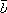 заданы
в этой системе своими координатами:
заданы
в этой системе своими координатами:
 ,
,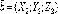 ,
,
то векторное произведение вектора
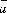 на
вектор
на
вектор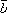 определяется
формулой
определяется
формулой
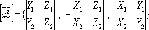 ,
,
или
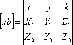
Векторное произведение применяется для вычисления площадей параллелограммов и треугольников.
Площадь параллелограмма, построенного
на векторах
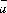 и
и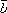 ,
равна:
,
равна:

 =
=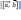
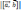 =
=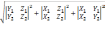
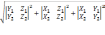 .
.
Если
третьи координаты равны нуля:
 ;
то формула будет выглядеть:
;
то формула будет выглядеть:

 =
=
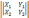 ;
;
Площадь треугольника ∆ABC равна половине площади параллелограмма: