
- •Линейная алгебра и геометрия.
- •1.Определители и их свойства.
- •2.Миноры и алгебраические дополнения. Теорема о разложении опред. По элементам строки или столбца.
- •3.Системы трех линейных уравнений с тремя неизвестными, правило Крамера.
- •4. Матрицы, действия над матрицами.
- •5. Теорема о ложном разложении опред. Вычисление произвед. Квадратной матрицы на ее присоединенную.
- •6.Обратная матрица. Матричный способ решения систем линейных уравнений.
- •7.Векторы. Сложение векторов и умножение их на число.
- •10.Система координат. Выражение координат вектора через координаты его конца и начала.
- •11. Деление отрезка в данном отношении.
- •12.Прямоугольная система координат. Длина вектора. Расстояние между двумя точками.
- •14.Скалярное произведение и его свойства.
- •16.Векторное произведение и его свойства. Геометрический смысл модуля.
- •17.Вычисление координат векторного произведения. Применение к вычислению площадей.
- •18 Смешанное произведение векторов и его геометрический смысл.
- •19 Вычисление смешанного произведения в координатах. Признак компланарности трех векторов
- •20. Уравнение прямой на плоскости, проходящей через данную точку перпендикулярно данному вектору.
- •21. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.
- •22. Уравнение плоскости, проходящей через данную точку параллельно двум данным векторам.
- •23. Уравнение плоскости проходящей через три данные точки.
- •24. Условие параллельности вектора и плоскости. Неполные уравнения плоскости.
- •25.Расстояние от точки до плоскости
- •26. Угол между двумя прямыми на плоскости. Условия параллельности и перпендикулярности прямых.
- •28.Уравнение прямой, проходящей через данную точку параллельно данному вектору. Угол между прямыми.
- •29. Приведение общих уравнений прямой в пространстве к каноническому виду.
- •30.Эллипс: геометрическое определение, вывод и исследование канонического уравнения
- •32.Парабола: геометрическое определение, вывод и исследование канонического уравнения
- •Дифференциальное исчисление.
- •1.Определение предела функции. Бесконечно малые. Представление функции в виде суммы константы и бесконечно малой.
- •2.Свойства бесконечно малых.
- •3. Предел суммы, произведения и частного.
- •4. Предел функции на бесконечности. Предел числовой последовательности.
- •5. Теорема о «двух милиционерах».
- •6. Первый замечательный предел.
- •7.Теорема о пределе монотонной ограниченной функции. Второй замечательный предел.
- •8. Сравнение бесконечно малых. Эквивалентные бесконечно малые.
- •9. Таблица эквивалентных бесконечно малых.
- •10.Непрерывность функции в точке. Односторонние пределы. Классификация точек разрыва.
- •13. Определение производной и ее геометрический смысл. Уравнение касательной и нормали к графику функции в данной точке.
- •14. Доказать, что дифференцируемая функция непрерывна.
- •15.Производная суммы и произведения функций.
- •17.Производная сложной функции.
- •20.Дифференциал функции: определение и формула для вычисления. Эквивалентность дифференцируемости и существования производной.
- •21.Теорема Ферма и Ролля.
- •23.Теорема коши об отношении приращений двух функций на отрезке
- •24.Правила Лопиталя
- •26.Возрастание и убывание функции. Доказать что, при положительной производной функция возрастает.
- •27.Точки экстремума,достаточное условие экстремума для первой производной.
- •28.Точки экстремума. Достаточное условие экстремума по второй производной.
- •29.Выпуклость и вогнутость ,точки перегиба связь со второй производной
- •31.Частные производные. Независимость смешанных частных производных от порядка дифференцирования.
- •32.Дифференцируемость функций нескольких переменных. Дифференциал функций.
- •33.Частные производные сложной функции.
- •34.Неявные функции и их производные.
- •35.Экстремумы функций двух переменных. Необходимое условие экстремума.
- •36.Достаточные условия экстремума функции двух переменных.
28.Точки экстремума. Достаточное условие экстремума по второй производной.
Функция y=f ( x ) называется возрастающей ( убывающей ) в некотором интервале, если при x 1 < x 2 выполняется неравенство f (x 1 ) < f (x 2 ) ( f (x 1 ) > f (x 2 )). Если дифференцируемая функция y = f ( x ) на отрезке [ a , b ] возрастает (убывает), то ее производная на этом отрезке f ¢ ( x ) > 0 ( f ¢ ( x ) < 0). Точка x о называется точкой локального максимума ( минимума ) функции f ( x ), если существует окрестность точки x о , для всех точек которой верно неравенство f ( x ) £ f ( x о ) ( f ( x ) ³ f ( x о )). Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами. Необходимые условия экстремума . Если точка x о является точкой экстремума функции f ( x ), то либо f ¢ ( x о ) = 0, либо f ¢ ( x о ) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек. Первое достаточное условие. Пусть x о - критическая точка. Если f ¢ ( x ) при переходе через точку x о меняет знак плюс на минус, то в точке x о функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке x о экстремума нет. Второе достаточное условие. Пусть функция f ( x ) имеет производную f ¢ ( x ) в окрестности точки x о и вторую производную в самой точке x о . Если f ¢ ( x о ) = 0, >0 ( <0), то точка x о является точкой локального минимума (максимума) функции f ( x ). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные. На отрезке [ a,b ] функция y = f ( x ) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [ a,b ].
29.Выпуклость и вогнутость ,точки перегиба связь со второй производной
Вторая
производная. Если
производная f
'
( x
) функции f
(
x
) дифференцируема в точке ( x0
), то её производная называется второй
производной функции
f
(
x
) в
точке ( x0
), и обозначается
f
'' (
x0
). Функция f
(
x
) называется выпуклой
на интервале ( a,
b
), если её график на этом интервале лежит
ниже
касательной, проведенной к кривой
y
= f (
x
) в любой точке ( x0
,
f
(
x0
) ), x0
 (a,
b
).
(a,
b
).
Функция
f
(
x
) называется вогнутой
на интервале ( a,
b
), если её график на этом интервале лежит
выше
касательной, проведенной к кривой
y
= f (
x
) в любой точке ( x0
,
f
(
x0
) ), x0
 (a,
b
).Достаточное
условие вогнутости ( выпуклости ) функции.
(a,
b
).Достаточное
условие вогнутости ( выпуклости ) функции.
Пусть
функция f
(
x
) дважды дифференцируема ( имеет вторую
производную ) на интервале ( a,
b
), тогда: если f
'' (
x
) > 0 для любого x
 (a,
b
), то функция f
(
x
) является вогнутой
на интервале ( a,
b);если
f
'' (
x
) < 0 для любого x
(a,
b
), то функция f
(
x
) является вогнутой
на интервале ( a,
b);если
f
'' (
x
) < 0 для любого x
 (a,
b
), то функция f
(
x
) является выпуклой
на интервале ( a,
b
) .
(a,
b
), то функция f
(
x
) является выпуклой
на интервале ( a,
b
) .
Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, что если в точке перегиба x0 существует вторая производная f '' ( x0 ), то f '' ( x0 ) = 0.
30.Асимптоты.Аси́мпто́та(отгреч.—
несовпадающий, не касающийся)кривойсбесконечнойветвью —прямая,
обладающая тем свойством, что расстояние
от точки кривой до этойпрямойстремится к нулю при удалении точки
вдоль ветви вбесконечность[2].
Термин впервые появился уАполлония
Пергского, хотя асимптотыгиперболыисследовал ещёАрхимед
.Вертикальная асимптота —прямаявида при
условии существованияпредела
при
условии существованияпредела .Как
правило, при определении вертикальной
асимптоты ищут не один предел, а два
односторонних (левый и правый). Это
делается с целью определить, как функция
ведёт себя по мере приближения к
вертикальной асимптоте с разных сторон.
Например:
.Как
правило, при определении вертикальной
асимптоты ищут не один предел, а два
односторонних (левый и правый). Это
делается с целью определить, как функция
ведёт себя по мере приближения к
вертикальной асимптоте с разных сторон.
Например:

 Замечание:
обратите внимание на знаки бесконечностей
в этих равенствах.
Замечание:
обратите внимание на знаки бесконечностей
в этих равенствах.
ГоризонтальнаяГоризонтальная
асимптота — прямая
вида  при
условии существованияпредела
при
условии существованияпредела
 .
.
НаклоннаяНаклонная
асимптота — прямая
вида  при
условии существованияпределов
при
условии существованияпределов
Замечание:
функция может иметь не более двух
наклонных(горизонтальных) асимптот!Замечание:
Если хотя бы один из двух упомянутых
выше пределов не существует (или равен
 ),
то наклонной асимптоты при
),
то наклонной асимптоты при (или
(или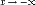 )
не существует!
)
не существует!
Связь между наклонной и горизонтальной асимптотами
Если
при вычислении предела  ,
то очевидно, что наклонная асимптота
совпадает с горизонтальной. Какова же
связь между этими двумя видами асимптот?
,
то очевидно, что наклонная асимптота
совпадает с горизонтальной. Какова же
связь между этими двумя видами асимптот?
Дело
в том, что
горизонтальная асимптота является
частным случаем наклонной
при  ,
и из выше указанных замечаний следует,
что
,
и из выше указанных замечаний следует,
что
Функция имеет или только одну наклонную асимптоту, или одну горизонтальную асимптоту, или одну наклонную и одну горизонтальную, или две наклонных, или две горизонтальных, либо же вовсе не имеет асимптот.
Существование указанных в п. 1. асимптот напрямую связано с существованием соответствующих пределов.


