Линейная алгебра и геометрия.

1.Определители и их свойства.

Определителем квадратной матрицы А=() наз. число и обозначается |А| и сопоставляется матрице А по определенному правилу.

1)опред. первого порядка( n=1),т. е. опр. Матрицы А=(a), наз. само число a , которое стоит в этой матрице |А|=a.

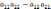
2)опред. второго порядка (n=2), т. е. опред. матрицы А=, наз. число |А|==равное разности произведений элементов главной и побочной диагоналей.

3)опред. третьего порядка(n=3),т.е. опред. матрицы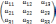 А=наз. число, определяемое по формуле |А|=.

Правило треугольников(правило Саррюса)

«+» «-»

Свойства определителей:(для любого порядка)

|А|=() и в виде набора трех ее строк |А|=˂˃

1)кососиметричность. Если в определителе поменять местами какие-либо две строки, то опред. изменит знак. ˂˃=- ˂˃.

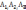2)если в определителе какая-то строка, например первая, представляется в виде суммы двух строк : 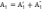, то определитель равен сумме двух опред. ˂˃=˂˃+˂˃

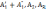3)если какую-то строку опред. умножить на число, то опред. умножится на это число.(общий множитель строки можно вынести за знак определителя)

˂

1-3 – основные правила

4)если в опред. две строки равны, то опред. равен нулю.

5)если в опред. какие-то две строки пропорциональны , то опред. равен нулю.

Элементарные преобраз. Первого рода i-ую и j-ую строки меняют местами,

Вторго рода: к i-ой строке прибавляется j-ая, умноженная на число λ

6)при элементарных преобразованиях второго рода опред. не меняется

7)при транспонировании опред. не меняется.

2.Миноры и алгебраические дополнения. Теорема о разложении опред. По элементам строки или столбца.

Минором элементаопред. |А| порядкаn назыв. опред. порядка n-1, который получается вычеркиванием из А строки и столбца, в которой стоит элемент А=,=||

Алгебр. Дополнени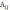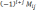е =, т. е.=

Для опред. третьего порядка знаки таковы

Теорема. Опред. равен сумме произведений элементов какой-то строки(столбца) на соответствующие алгебраич. дополнения. Например: разложение опред. третьего порядка по первой строке:|А|=

Док-во

Сгруппируем и вынесем за скобки:|А|===

3.Системы трех линейных уравнений с тремя неизвестными, правило Крамера.

Системой m линейных уравнений с n неизвестными наз. система вида

Решением системы наз. набор чисел. Решить систему значит найти все ее решения., если имеется хотя бы 1 решение-совместная, иначе несовместной. если единственное решение-определенная ,две системы наз. эквивалентными(если имеют одинаковые решения.)

Обозначим через Δ опред. Системы , а через ,i=1,2,3

Δ=|A|=,Δ1=,Δ2=,Δ3=.

Правило Крамера: теорема. 1)если опред. системы Δ‡0, то система совместна и определена, и ее единственное решение находится (в случае n=3) по формулам Крамера: ,,

2) если Δ=0, а хотя бы один из ‡0, то система несовместна.

Если n=2, то теорема:для системы линейных уравнений второго порядка возможны 3 случая: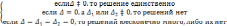

4. Матрицы, действия над матрицами.

Матрицей типа mxn наз. таблица с m строками и n столбцами.

Матрица типа mx1 наз. вектор-столбцом, а матрица типа 1 xn –вектор строкой

Матрица, у которой число строк равно числу столбцов m=n наз. квадратной матрицей порядка n.

Диагональ квадратной матрицы, на которой стоят элементы наз. главной, а другая-побочной .

1)транспонироавание. матрица , полученная из исходной матрицы A заменой строк на столбцы.

A=(2*3)матрица ,=,(3*2)

2)сложение матриц и умножение на число.

Произведением матрицы А на число λ наз. матрица λА=(λ)при умножении матрицы на число все ее элементы умножаются на это число.

Суммой матриц А=() иB=() одного и того же типаmxn наз. (mxn)- матрица С=А+B элементы складываются ,стоящие на одинаковых местах.