
- •Конспект лекций
- •Введение
- •Лекция 1. Информация и информационные технологии. Основные понятия. Предмет информатики
- •Информация Определение и измерение информации
- •Свойства информации
- •Информация и данные
- •Кодирование данных в компьютере
- •Измерение компьютерных данных
- •Лекция 2 Арифметические основы компьютеров Системы счисления
- •Перевод чисел в десятичную систему счисления
- •Поразрядный перевод чисел из одной системы счисления в другую
- •Перевод целых десятичных чисел в другую систему счисления
- •Перевод правильной десятичной дроби в другую систему счисления
- •Двоичная арифметика
- •Представление чисел в компьютере Целые числа без знака
- •Целые числа со знаком
- •Вещественные числа
- •Лекция 3 Технические средства информационных технологий Классификация
- •Устройство персонального компьютера
- •Системный блок
- •Материнская плата
- •Центральный процессор
- •Архитектура процессора
- •Система команд процессора
- •Оперативная память
- •Постоянная память
- •Лекция 4
- •Операционные системы
- •Файловая система. Основные определения
- •Операционная система ms dos
- •Загрузка компьютера с операционной системой ms dos
- •Командный язык операционной системы msdos и Windows
- •Dir [дисковод] [путь] [ключи]
- •Md [дисковод:] [путь]
- •Copy [дисковод:] полное_имя_1 [дисковод:] полное_имя_2
- •Ren [дисковод:] имя файла1 имя файла2
- •Линейный алгоритм
- •Ветвящийся алгоритм
- •Циклический алгоритм
- •Алгоритмы накопления суммы и произведения
- •Алгоритм табулирования функции
- •Алгоритм поиска экстремальных значений (max, min)
- •Лекция 6 Язык программирования Microsoft Qbasic Набор символов языка:
- •Классификация данных
- •Ограничения значений переменных
- •Операции
- •Выражения
- •Стандартные функции действия над числами
- •Операторы
- •Оператор восстановления данных restore
- •Оператор input
- •Input считывает входные данные от клавиатуры или из файла.
- •Input ["приглашение"{; | ,}] список переменных
- •Вывод данных Операторы print, lprint, print using, функции spc и tab
- •Функции spc и tab
- •Тав: print tab (выражение1); выражение2
- •Оператор форматированного вывода
- •Print using формат; список выражений [{;|,}]
- •Оператор позиционирования курсора locate
- •Лекция 7 Управление ходом выполнения программы Организация цикла
- •Оператор цикла for … next
- •Оператор цикла do … loop
- •Print "Значение I в конце цикла равно "; I
- •Оператор цикла без счетчика while …wend
- •Операторы изменения хода выполнения программы
- •Оператор выбора select case
- •Оператор exit
- •Оператор swap
- •Функции действия над строками
- •Лекция 8 Алгоритмы решения математических задач Решение уравнений методом итерации
- •Решение уравнений методом простой итерации
- •Input “Введите точность”, e
- •Input “Введите начальное значение х”, х
- •Input “Введите точность”, e
- •Input “Введите начальное значение х”, х
- •Итерационное решение уравнений методом половинного деления
- •Input “Введите точность”, e
- •Оператор описания массивов Одномерные массивы
- •Статические и динамические массивы
- •Оператор option base
- •Способы ввода значений элементов массива
- •Оператор rnd
- •Randomize [число].
- •Алгоритм формирования и печати исходного массива
- •Алгоритм поиска максимального и минимального значений в массиве s(n)
- •Алгоритмы сортировки массива Сортировка выбором мах (или мin)
- •Сортировка вставками
- •Метод «пузырька»
- •Лекция 10 Описание и обработка матриц
- •Input “ введите значение”, a(I,j)
- •Лекция 11 Алгоритмы компьютерной графики
- •Текстовый режим
- •Операторы графики
- •Построение графиков математических функций
- •Этапы построения графика функции
- •Оператор circle вывода окружностей, дуг, эллипсов
- •Circle (X, y), r, [цвет], [Dn], [Dk], [z]
- •Цвет в графике
- •Оператор рисования объекта.
- •Построение диаграмм
- •Этапы работы при создании рисунка
- •Эффект мультипликации
- •Лекция 13 Работа с файлами Назначение файлов
- •Физическая и логическая организации файлов
- •Способы доступа к файлам
- •Действия с файлами
- •Оператор open открытия файла
- •Режимы работы с файлами
- •Номер файла
- •Чтение данных из файла прямого доступа и бинарного файла оператором get
- •Get [#]номер_файла [,[номер_записи][, переменная]] ,
- •Чтение данных из файла последовательного доступа оператором input
- •Запись данных в файл прямого доступа и бинарный файл оператором put
- •Закрытие файла
- •Удаление файлов
- •Лекция 14 Приемы модульного программирования
- •Процедуры
- •Input “Введите размерность массива ”; n
- •Процедурные языки (с, basic, fortran, pascal и др.)
- •Функциональные языки
- •Логические языки (лисп, пролог)
- •Трансляторы
- •Лекция 15 Разработка сложных программ
- •Методологии и технологии проектирования ис Общие требования к методологии и технологии
- •Лекция 16 Компьютерные сети. Архитектура построения
- •Масштабы компьютерных сетей
- •Топологии компьютерных сетей
- •Топология типа «звезда»
- •Коммутируемая топология
- •Сложные топологии
- •Методы передачи компьютерных данных Кадры и протоколы
- •Кадр Ethernet стандарта ieee 802.3
- •Кадр Token Ring стандарта 802.5
- •Примеры протоколов.
- •Лекция 17 Основные компоненты компьютерных сетей
- •Линии связи
- •Коммуникационное оборудование
- •Литература
- •Словарь понятий
Линейный алгоритм
Линейным называют алгоритм, операции и линии потоков которого идут по одному направлению, без повторений операций, без альтернативных путей потоков.
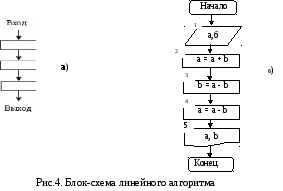 Блок-схема
такого алгоритма имеет вид, представленный
на рис. 4 а.
Пример линейного алгоритма:
имеются две переменные a
и b,
произвести обмен их значениями. Блок-схема
алгоритма решения этой задачи приведена
на рис. 4 б.
Блок-схема
такого алгоритма имеет вид, представленный
на рис. 4 а.
Пример линейного алгоритма:
имеются две переменные a
и b,
произвести обмен их значениями. Блок-схема
алгоритма решения этой задачи приведена
на рис. 4 б.
Следует отметить, что знак «=» в блоках 2, 3 и 4 означает не равенство, а операцию присвоения переменной значения. Например, в блоке 2 производится присвоение переменной а суммы значений переменных а и b.
В блок-схеме алгоритма все операции нумеруются (номер проставляется вверху слева от блока) в порядке их выполнения. Блоки «Начало» и «Конец» не нумеруются.
Ветвящийся алгоритм
Алгоритм называется ветвящимся (см. рис. 5), если в нем содержится блок перехода или условия, который имеет одну входную линию потока и более одной выходные линии.
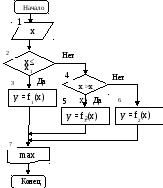
Пример ветвящегося алгоритма: найти наибольшее значение трех переменных a, b и c. Блок-схема решения этого алгоритма приведена на рис. 6.
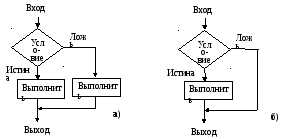
Рис. 5. Блок-схема ветвящегося алгоритма; а – полное ветвление, б – непол-ное ветвление.
Р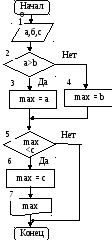 ис.
6 . Блок схема алгоритма поиска
максимального из трех значений
ис.
6 . Блок схема алгоритма поиска
максимального из трех значений
На рис. 7 приведен пример алгоритма вычисления значения переменной у, определяемой математическим выражением:
|
у = |
f f2(x) если x1 ≤ x ≤ x2 f3(x) если x > x2
|
Рис. 7. Пример ветвящегося алгоритма
Циклический алгоритм
Алгоритм называется циклическим, если он содержит в своем составе последовательность действий (операторов, переходов), неоднократно повторяющуюся с заданием новых начальных условий. При этом алгоритм включает в себя процедуры задания этих начальных условий.
Часть алгоритма, отражающая эти действия, называется циклом
Как
правило, алгоритмы решения реальных
задач представляют собой комбинацию
всех трех рассмотренных типов простейших
алгоритмов. Рассмотрим алгоритмы
некоторых часто встречающиеся задач.Р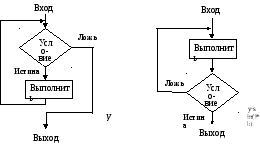 ис.
8. Циклический алгоритм; а – цикл «пока»,
б – цикл «до».
ис.
8. Циклический алгоритм; а – цикл «пока»,
б – цикл «до».
Алгоритмы накопления суммы и произведения
В
алгоритмах часто приходится накапливать
сумму и произведение значений функции.
Математическая запись суммы имеет вид
![]() произведения -
произведения -![]() гдеNn
– начальные значений переменной, Nk
– конечное значение целочисленной
переменной i.
гдеNn
– начальные значений переменной, Nk
– конечное значение целочисленной
переменной i.
Перед началом процесса накопления суммы переменной, в которой будет использоваться сумма, необходимо присвоить значение 0. Иначе при объявлении переменной и выделения места в памяти ЭВМ, в этом месте может оказаться любая информация от предыдущих операций, и мы можем получить неверную сумму.
При подсчете произведения переменной, в которой будет накапливаться произведение, необходимо присвоить начальное значение 1.
Р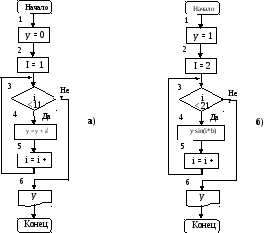 ис.
9. Блок схемы алгоритмов накопления
ис.
9. Блок схемы алгоритмов накопления
а)
– суммы y
=
![]() ai
и б) - произведения y
=
ai
и б) - произведения y
=
![]() sin(I*b)
sin(I*b)
Алгоритм табулирования функции
Табулирование функции – это вычисление ее значений по изменяющимся значениям аргумента функции.
Табулируют функцию, например, для построения ее графика, для поиска ее максимальных значений. Табулирование функции y = f(x) ведется на некотором интервале значений аргумента x € [хн; хк], с изменением значений аргумента на одинаковую величину ∆х, которую называют шагом изменения х.
П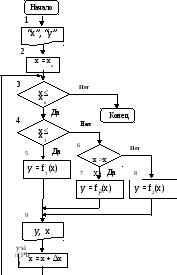 ример.
Разработать алгоритм табулирования
функции y,
приведенной на стр. 44, на интервале
значений х € [хн;
хк],
с шагом ∆х изменения аргумента.
Блок-схема алгоритма решения этой
задачи приведена на рис. 10.
ример.
Разработать алгоритм табулирования
функции y,
приведенной на стр. 44, на интервале
значений х € [хн;
хк],
с шагом ∆х изменения аргумента.
Блок-схема алгоритма решения этой
задачи приведена на рис. 10.
Рис. 11. Блок-схема алгоритма табулирования функции
“Блок 1” обеспечивает печать заголовка таблицы, а блок 9 – строк таблицы, чтобы получить таблицу следующего вида:
|
x |
y |
|
хн |
yн |
|
х + ∆х |
yн+1 |
|
x + 2∆х |
yн+2 |
|
… |
… |
|
хк - ∆х |
yк-1 |
|
xк |
yк |
“Блок 2”, “Блок 3” и “Блок 10” обеспечивают цикличность вычисления y в соответствии с изменением значения аргумента х от начального значения хн до конечного значения хк с шагом ∆х.

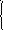
 1(x)
если x
≤ x1
1(x)
если x
≤ x1