СЛАУ

РЕШЕНИЕ ОТЫСКИВАЕТСЯ В ВИДЕ:

i, i –ПРОГОНОЧНЫЕ КОЭФФИЦИЕНТЫ

41

МЕТОД ПРОГОНКИ

2 ЭТАПА

•ПРЯМОЙ: ИЩЕМ ПРОГОНОЧНЫЕ КОЭФФИЦИЕНТЫ

•ОБРАТНЫЙ: ИЩЕМ РЕШЕНИЕ

42

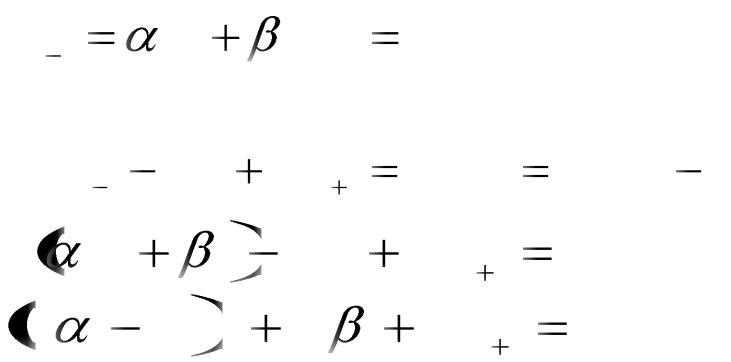
МЕТОД ПРОГОНКИ

ПО ЭТИМ ФОРМУЛАМ ВЫЧИСЛЯЮТ ВСЕ ПРОГОНОЧНЫЕ КОЭФФИЦИЕНТЫ

i , i ,i 2,...,n

44

МЕТОД ПРОГОНКИ

ПРЯМОЙ ЭТАП: НАХОДИМ КОЭФФИЦИЕНТЫ

ОБРАТНЫЙ ЭТАП: НАХОДИМ РЕШЕНИЕ

46

МЕТОД ПРОГОНКИ

ТЕОРЕМА. ПУСТЬ КОЭФ-ТЫ ai, bi, ci ОТЛИЧНЫ ОТ НУЛЯ И УДОВЛЕТВОРЯЮТ УСЛОВИЮ:

ТОГДА ПРОГОНКА КОРРЕКТНА И УСТОЙЧИВА.

ПРИ ЭТИХ УСЛОВИЯХ:

•ЗНАМЕНАТЕЛЬ ФОРМУЛ НЕ ОБРАТИТСЯ В 0,

•ОШИБКИ ОКРУГЛЕНИЯ НЕ БУДУТ НАКАПЛИВАТЬСЯ

УСЛОВИЕ ДИАГОНАЛЬНОГО ПРЕОБЛАДАНИЯ

47

ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ

Преобразуем исходную систему линейных уравнений

Ax b

к виду:

x α x β

α– порождающая матрица, – вектор.

Будем решать методом ПРОСТОЙ ИТЕРАЦИИ.

48

МЕТОД ПРОСТОЙ ИТЕРАЦИИ

Зададим вектор начального приближения:

Следующие приближения ищем по формулам:

Итерации останавливаем, когда невязка r станет меньше

49

МЕТОД ЯКОБИ

МАТРИЦА МЕТОДА:

ДОСТАТОЧНОЕ УСЛОВИЕ СХОДИМОСТИ МЕТОДА:

условие диагонального преобладания для исходной матрицы A :

j1 i j

50