8.4. Измерение неприступных расстояний

При выполнении измерительных работ нередко возникают ситуации, когда та или иная линия не может быть измерена непосредственно (водные преграды, непроходимые болота и т.д.). В этих случаях, в зависимости от того, какими техническими средствами располагает исполнитель (землемерными лентами и рулетками, оптическими теодолитами, светодальномерами, лектроными тахеометрами, приборами спутниковой навигации «GPS» и т.д.), неприступное расстояние может быть определено одним из следующих способов: базисов; равных треугольников; прямого промера по оси; наземно – космическим.

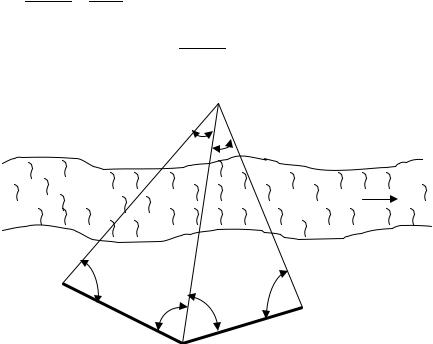
Способ базисов состоит в измерении неприступного расстояния с помощью прямой угловой засечки (рис. 54).

На удобных участках местности для производства линейных измерений с использованием землемерной ленты или рулетки от точки А измеряемой линии строят два базиса в1 и в2 таким образом, чтобы между ними и измеряемой прямой линией образовались два треугольника с углами при основании не менее 30˚ и не более 150˚. Базисы измеряют землемерной лентой или рулеткой дважды и при допустимых расхождениях в промерах определяют среднее значение каждого из них. Полным приемом теодолита измеряют горизонтальные углы при основаниях полученных треугольников АВС1 и АВС2, соответственно γ1; α1; γ2; α2. По теореме синусов дважды определяют значение искомого неприступного расстояния:

Если относительная погрешность между двумя измерениями не превышает

Ав2

Рис. 54

57