- •Глава 5. Анализ временных последовательностей в сфере управления
- •5.1. Структура временных последовательностей и основные приемы анализа компонентов рядов динамики
- •- Для аддитивной модели
- •- Для мультипликативной модели
- •5.2. Прогнозирование во временных рядах
- •5.3. Анализ пространственно-временных (панельных) данных
5.3. Анализ пространственно-временных (панельных) данных
В главе 2 отмечалось, что существуют два типа данных: пространственные данные (cross-sectional data) и временные ряды (time-series data). Однако наиболее часто исследователь встречается с пространственно-временными данными, которые являются одновременно и пространственными, и временными. Другое их название – панельные данные. Примером пространственно-временных данных является набор статистических показателей социально-экономического развития регионов страны или федеральных округов, представленных за ряд лет. Для исследователя наибольший интерес представляет анализ именно таких данных.
В анализе пространственно-временных данных особенно важна рациональная организация пространственных данных в электронные таблицы: территориальные образования должны составлять блоки строк таблицы, отвечающие различным территориальным образованиям, а столбцы – представлять различные показатели для этих территориальных образований в различные моменты времени. Нами предлагается для удобства анализа ввести новый термин, обозначающие территориальное образование по состоянию на данный момент времени или за данный временной интервал. Если время измеряется в годах, то в региональном разрезе это годорегион, в разрезе федеральных округов – годоокруг и т.д. Такое представление позволяет строить и временные, и пространственные модели. В частности, появляется возможность построения годографов, отражающих эволюцию территориальных образований во времени; примеры применения таких годографов в аналитических целях приведены в [219].
Особый интерес представляет замена пространственно-временных данных набором параметров эконометрических моделей, аппроксимирующих соответствующие временные ряды. В случае их адекватности такая замена позволяет выполнить глубокий анализ территориальных особенностей и уровня показателей, и динамики их изменения, что в большинстве случаев приводит к получению новых знаний об исследуемых процессах.
Пример представления пространственно-временных данных в виде фрагмента электронной таблицы, импортированной из программы SPSS Base, приведен на рис. 5.15.
Поясним структуру этой электронной таблицы. Ее столбцами являются федеральные округа, годоокруга, годы и показатель – в данном случае, заболеваемость населения. Такая структура электронной таблицы позволяет строить графики Парето и территориальные профили, а также графики временных рядов. Можно строить и годографы, отражающие эволюцию того или иного территориального образования в отношении изучаемых показателей во времени.
-
Заболеваемость,
Федеральный Год промилле
округ Годоокруг Mean Mean
___________ __________ ________ _______________
ЦФО ЦФО-2000 2000 708,5
ЦФО-2001 2001 704,8
ЦФО-2002 2002 715,1
ЦФО-2003 2003 733,2
ЦФО-2004 2004 720,9
ЦФО-2005 2005 706,5
ЦФО-2006 2006 718,3
ЦФО-2007 2007 722,8
…
УФО УФО-2000 2000 791,1
УФО-2001 2001 749,6
УФО-2002 2002 765,2
УФО-2003 2003 778,4
УФО-2004 2004 774,1
УФО-2005 2005 779,9
УФО-2006 2006 802,5
УФО-2007 2007 813,1
…
Рис. 5.15. Фрагмент электронной таблицы, импортированной из программы SPSS Base
В качестве примера на рис. 5.16 представлены диаграммы, отражающие ранжирование федеральных округов по уровню заболеваемости населения в два момента времени – в 2000 и 2007 гг., а на рис. 5.17 – графики временных рядов заболеваемости населения в Центральном и Северо-Западном федеральных округах, при этом для наглядности сравнения на графиках принят одинаковый масштаб.
Анализируя диаграммы рис. 5.16, можно заключить, что заболеваемость населения сильно определяется географическими условиями и национальными особенностями: меньше всего уровень заболеваемости в Южном федеральном округе, больше всего – в Приволжском федеральном округе.
|
а |
б |
|
|
|
|
Рис. 5.16. Ранжирование федеральных округов по уровню заболеваемости населения в 2000 г. (а) и 2007 г. (б). Пунктир – уровень РФ | |
В период 2000-2007 гг. заболеваемость во всех федеральных округах увеличивалась, но в различной степени – рис. 5.17, меньшей в ЦФО и большей в СЗФО.
|
а |
б |
|
|
|
|
Рис. 5.17. Динамика заболеваемости населения в 2000-2007 гг. Центрального (а) и Северо-Западного (б) федеральных округов | |
Для построения годографов, отражающих эволюцию того или иного территориального образования в отношении изучаемых показателей во времени, необходимо располагать данными не по одному, а как минимум по двум показателям. В качестве примера рассмотрим эволюцию Центрального федерального округа и Российской Федерации в целом в период 2005-2008 гг. по двум парам показателей здоровья – продолжительности жизни и общего коэффициента рождаемости, с одной стороны (они коррелируют с демографическим фактором) и уровня заболеваемости (коррелирует с фактором трудоспособности), с другой – рис. 5.18 и рис. 5.19.
|
а |
б |
|
|
|
|
Рис. 5.18. «Дрейф» Центрального федерального округа (а) и Российской Федерации (б) на плоскости ожидаемой продолжительности жизни при рождении и заболеваемости на 1000 человек | |
|
а |
б |
|
|
|
|
Рис. 5.19. «Дрейф» Центрального федерального округа (а) и Российской Федерации (б) на плоскости общего коэффициента рождаемости и заболеваемости на 1000 человек | |
По характеру годографов, представленных на этих рисунках, видно, что и в ЦФО, и в РФ в целом, в рассматриваемый период позитивные показатели здоровья (продолжительность жизни, общий коэффициент рождаемости) увеличиваются, но возрастает также негативный показатель – уровень заболеваемости.
Еще один способ представления панельных данных – замена временных рядов параметрами моделей, аппроксимирующих эти ряды. Рассмотрим этот способ на примере анализа территориальных различий такого важного показателя социально-экономического развития регионов Центрального федерального округа, как ввод в действие жилых домов на 1000 человек населения. В статистических изданиях эти данные приведены в региональном и временном разрезах в квадратных метрах жилой площади, и это позволяет рассмотреть как динамику развития строительной отрасли, так и ее региональную дифференциацию.
Рассмотрим динамику ввода в действие жилых домов на 1000 человек населения в целом в РФ и в ЦФО – рис. 5.20. Видно, что в начале рассматриваемого периода в стране и Центральном федеральном округе наблюдалось спад строительства жилых домов, затем – рост показателя примерно по экспоненте, сменившийся в 2008 году замедлением и даже снижением ввода в действие жилых домов на 1000 человек населения.
|
а |
б |
|
|
|
|
Рис. 5.20. Динамика ввода в действие жилых домов на 1000 человек населения: а – в РФ в целом; б – в ЦФО | |
Рассматриваемый показатель измерен в квадратных метрах жилой площади, и в расчете территориальных индексов нет особой необходимости, поэтому перейдем непосредственно к анализу динамики региональных данных в период 2000-2007 гг., для которого и в РФ в целом, и в ЦФО наблюдался устойчивый рост строительной индустрии.
На рис. 5.21 приведены графики временных рядов ввода в действие жилых домов на 1000 человек населения в ряде регионов ЦФО.
|
а |
б |
|
|
|
|
Рис. 5.21. Динамика ввода в действие жилых домов на 1000 человек населения в ряде регионов ЦФО | |
Из хода графиков временных рядов, представленных на рис. 5.21, можно предположить, что в период 2000-2007 гг. динамика этого показателя, за некоторыми исключениями (Брянская, Костромская и Тульская области), может быть вполне удовлетворительно описана законом экспоненциального роста
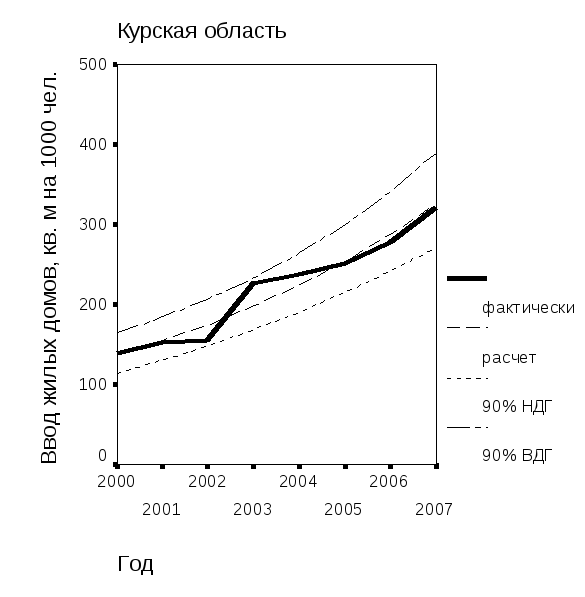
Результаты аппроксимации экспоненциальными моделями динамики ввода в действие жилых домов на 1000 человек населения в двух регионах ЦФО – Курской и Московской области, представленные на рис. 5.22, подтверждают это предположение. Видно, что ширина доверительного интервала в обоих случаях находится в приемлемых размерах; удовлетворительными являются и характеристики качества аппроксимации: коэффициент детерминации равен 0,945 и 0,966 соответственно, критерий Фишера, равный 103,9 и 169,2 соответственно, статистически значим на уровне не хуже 0,001.
|
а |
б |
|
|
|
|
Рис. 5.22. Аппроксимация динамики ввода в действие жилых домов на 1000 человек населения моделью экспоненциального роста: а – Курская область; б – Московская область | |
Явный вид этих моделей следующий:
- для Курской области
Vжил = 136,82 × exp (0,1236 t); (5.48)
- для Московской области
Vжил = 385,85 × exp (0,1595 t), (5.49)
где t – временная переменная, определяемая соотношением
t = год – 2000. (5.50)
Оба параметра моделей (5.48) и (5.49) имеют четкий экономический смысл: свободные коэффициенты 136,82 и 385,85 – это расчетные значения объемов ввода в действие жилых домов в кв. м жилой площади на 1000 человек населения в Курской и Московской области соответственно в начальный год рассматриваемого периода (2000 г.), 0,1236 и 0,1595 – МНК-оценки коэффициента прироста показателя.
Результаты расчета параметров динамики приведены в табл. 5.8. Видно, что модели для Брянской, Костромской и Тульской областей объясняют меньше 50% дисперсии, и на этом основании они не могут быть признаны адекватными эмпирическим данным. Однако после увеличения временного интервала до 2009 г. экспоненциальные модели для Брянской и Тульской областей становятся уже адекватными, а для Костромской области в качестве адекватной принимается модель среднего значения.
Лучше, однако, говорить не о коэффициентах прироста, а о темпах роста показателя, равных 112,36% и 115,95% в Курской и Московской области соответственно. Представляется также целесообразным расчетные значения объемов ввода в действие жилых домов в кв. м жилой площади на 1000 человек населения в 2000 г. заменить расчетными значениями показателя в 2007 году.
Таблица 5.8
Параметры и критерии качества экспоненциальных моделей динамики объемов ввода в действие жилых домов в кв. м жилой площади на 1000 человек населения в 2000-2007 гг.
|
Регион |
Код |
МНК-оценки параметров |
Критерии качества | |||
|
расчетный уровень показателя в 2000 г., кв. м |
среднегодовой коэффициент прироста, % |
коэффициент детерминации |
критерий Фишера |
уровень значимости (р-уровень) | ||
|
Белгородская обл. |
1 |
398,226 |
0,0710 |
0,804 |
24,64 |
0,003 |
|
Брянская обл. |
2 |
155,865 |
0,0299 |
0,323 |
2,87 |
0,141 |
|
Владимирская обл. |
3 |
158,703 |
0,0657 |
0,852 |
34,53 |
0,001 |
|
Воронежская обл. |
4 |
230,533 |
0,0820 |
0,955 |
128,18 |
0,000 |
|
Ивановская обл. |
5 |
76,661 |
0,0768 |
0,526 |
6,66 |
0,042 |
|
Калужская обл. |
6 |
153,740 |
0,1155 |
0,799 |
23,89 |
0,003 |
|
Костромская обл. |
7 |
187,257 |
-0,0304 |
0,092 |
0,61 |
0,466 |
|
Курская обл. |
8 |
136,824 |
0,1236 |
0,945 |
103,90 |
0,000 |
|
Липецкая обл. |
9 |
235,080 |
0,1220 |
0,839 |
31,18 |
0,001 |
|
Московская обл. |
10 |
385,852 |
0,1595 |
0,966 |
169,17 |
0,000 |
|
Орловская обл. |
11 |
262,661 |
0,0332 |
0,601 |
9,05 |
0,024 |
|
Рязанская обл. |
12 |
155,401 |
0,1139 |
0,801 |
24,16 |
0,003 |
|
Смоленская обл. |
13 |
159,151 |
0,1033 |
0,925 |
73,75 |
0,000 |
|
Тамбовская обл. |
14 |
168,865 |
0,1277 |
0,930 |
80,10 |
0,000 |
|
Тверская обл. |
15 |
147,519 |
0,0930 |
0,923 |
72,19 |
0,000 |
|
Тульская обл. |
16 |
100,710 |
0,0757 |
0,414 |
4,23 |
0,085 |
|
Ярославская обл. |
17 |
95,858 |
0,1397 |
0,880 |
44,08 |
0,001 |
|
г. Москва |
18 |
355,913 |
0,0441 |
0,838 |
31,01 |
0,001 |
|
ЦФО |
100 |
259,336 |
0,0998 |
0,983 |
346,37 |
0,000 |
|
РФ |
1000 |
194,470 |
0,1014 |
0,960 |
143,07 |
0,000 |
В табл. 5.9 приведены параметры динамики объемов ввода в действие жилых домов в кв. м жилой площади на 1000 человек населения, пересчитанные с учетом сказанного выше.
Таблица 5.9
Параметры и критерии качества экспоненциальных моделей динамики объемов ввода в действие жилых домов в кв. м жилой площади на 1000 человек населения в 2000-2007 гг.
|
Регион |
Код |
МНК-оценки параметров |
Критерии качества | |||
|
расчетный уровень показателя в 2007 г., кв. м |
среднегодовой темп роста, % |
коэффициент детерминации |
критерий Фишера |
уровень значимости (р-уровень) | ||
|
Белгородская обл. |
1 |
654,45 |
107,10 |
0,804 |
24,64 |
0,003 |
|
Брянская обл. 1) |
2 |
215,26 |
105,50 |
0,653 |
15,06 |
0,005 |
|
Владимирская обл. |
3 |
251,29 |
106,57 |
0,852 |
34,53 |
0,001 |
|
Воронежская обл. |
4 |
409,15 |
108,20 |
0,955 |
128,18 |
0,000 |
|
Ивановская обл. |
5 |
131,20 |
107,68 |
0,526 |
6,66 |
0,042 |
|
Калужская обл. |
6 |
345,05 |
111,55 |
0,799 |
23,89 |
0,003 |
|
Костромская обл. 2) |
7 |
185,80 |
100,00 |
- |
- |
- |
|
Курская обл. |
8 |
324,97 |
112,36 |
0,945 |
103,90 |
0,000 |
|
Липецкая обл. |
9 |
552,02 |
112,20 |
0,839 |
31,18 |
0,001 |
|
Московская обл. |
10 |
1178,34 |
115,95 |
0,966 |
169,17 |
0,000 |
|
Орловская обл. |
11 |
331,31 |
103,32 |
0,601 |
9,05 |
0,024 |
|
Рязанская обл. |
12 |
344,99 |
111,39 |
0,801 |
24,16 |
0,003 |
|
Смоленская обл. |
13 |
328,09 |
110,33 |
0,925 |
73,75 |
0,000 |
|
Тамбовская обл. |
14 |
412,92 |
112,77 |
0,930 |
80,10 |
0,000 |
|
Тверская обл. |
15 |
282,80 |
109,30 |
0,923 |
72,19 |
0,000 |
|
Тульская обл.1) |
16 |
195,72 |
110,49 |
0,678 |
16,86 |
0,003 |
|
Ярославская обл. |
17 |
254,89 |
113,97 |
0,880 |
44,08 |
0,001 |
|
г. Москва |
18 |
484,61 |
104,41 |
0,838 |
31,01 |
0,001 |
|
ЦФО |
100 |
521,69 |
109,98 |
0,983 |
346,37 |
0,000 |
|
РФ |
1000 |
395,41 |
110,14 |
0,960 |
143,07 |
0,000 |
Примечания: 1) по данным за 2000-2009 гг.
2) модель среднего значения в период 2000-2009 гг.
Представление о ранжировании регионов ЦФО по значениям параметров динамики объемов ввода в действие жилых домов в кв. м жилой площади на 1000 человек населения в 2000-2007 гг. дает рис. 5.41.
|
а |
б |
|
|
|
|
Рис. 5.41. Ранжирование регионов ЦФОпо значениям параметровдинамики объемов ввода в действие жилых домов в кв. м жилой площади на 1000 человек населения в 2000-2007 гг.: а – расчетное значение показателя в 2007 г.; б – среднегодовой темп роста показателя | |
Казалось бы, из диаграммы на рис. 5.41 а следует, что Московская область, характеризуемая расчетным значением показателя 1178,3 кв. м жилой площади на 1000 человек населения, является «выбросом», и данные по этому региону необходимо исключить из дальнейшего анализа. Однако проверка распределения данного параметра по критерию Колмогорова-Смирнова показала отсутствие статистически значимых отклонений от нормального закона.
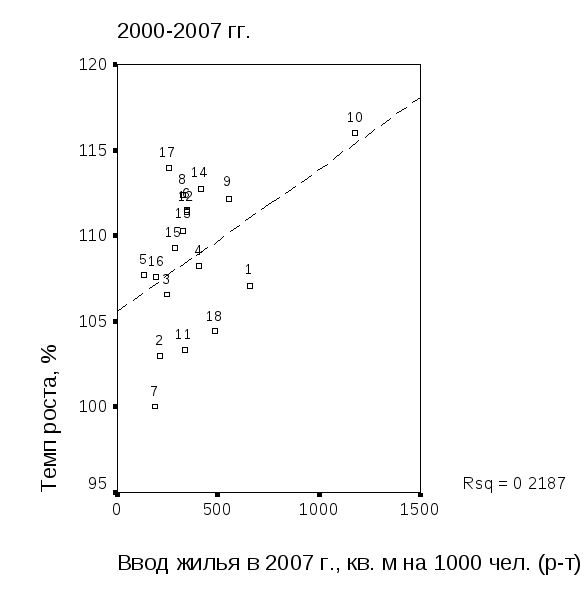
Заключительный этап статистических исследований параметров динамики объемов ввода в действие жилых домов в кв. м жилой площади на 1000 человек населения в 2000-2007 гг. – проверка на коррелированность. На рис. 5.42 представлены две диаграммы рассеяния – одна для параметров временных рядов динамики объемов ввода в действие жилых домов, вторая – для z-преобразованных значений. Из диаграммы рис. 5.42 а следует, что статистически значимая корреляция между параметрами динамики отсутствует, и на этом основании в множестве индикаторов, определяющих строительный потенциал регионов ЦФО, целесообразно сохранить оба показателя.
|
а |
б |
|
|
|
|
Рис. 5.42. Распределение регионов ЦФО: а – по расчетным значениям параметровдинамики объемов ввода в действие жилых домов в кв. м жилой площади на 1000 человек населения в 2000-2007 гг.; б – по их z-преобразованным значениям | |
Диаграмма на рис. 5.42 б иллюстрирует размещение регионов ЦФО относительно средних значений параметров динамики (числа над метками соответствуют кодам регионов в табл. 5.9): регионы центральной тенденции – это все регионы ЦФО, за исключением Костромской и Московской областей (метки 7 и 10 соответственно). Московская область характеризуется наилучшими значениями параметров динамики, Костромская область – нулевым значением темпа роста объемов ввода в действие жилых домов в кв. м жилой площади на 1000 человек населения в 2000-2009 гг.
Далеко не всегда удается описать пространственно-временные данные набором адекватных моделей одного вида. В этом случае можно воспользоваться принятым в теории статистики приемом – заменой временных рядов двумя параметрами: средним значением показателя и его среднегодовым приростом.
Рассмотрим этот прием на примере анализа динамики валового регионального продукта на душу населения в ЦФО. В официальных статистических источниках этот показатель, как правило, приводится в пространственном и временном разрезах.
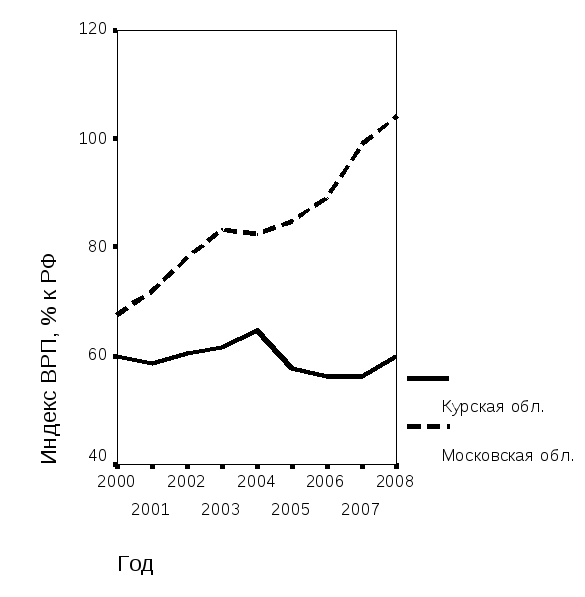
На этот показатель сильное влияние оказывают инфляционные процессы, и поэтому наряду с ВРП на душу населения, необходимо рассматривать территориальные индексы. Так, на рис. 5.43 а графики временных рядов ВРП для Курской и Московской областей носят характер экспоненциальных кривых, тогда как на рис. 5.43 б графики временных рядов индекса ВРП для Курской и Московской областей носят совершенно различный характер.
|
а |
б |
|
|
|
|
Рис. 5.43. Динамика региональных показателей: а – ВРП на душу населения; б – индекс ВРП на душу населения | |
В этом случае оптимальным вариантом описания данного важнейшего регионального показателя является замена пространственно-временных данных двумя параметрами: средним значением территориального индекса ВРП за период 2000-2008 гг. и среднегодовым приростом индекса – табл. 5.10.
Приведенные в табл. 5.10 данные получены с помощью процедуры Curve Estimation пакета статистических программ SPSS Base. Преимущество расчета с помощью этой процедуры в том, что, помимо МНК-оценок параметров линейных моделей, мы получаем характеристики их качества.
Поясним последнее. Для Московской области получена следующая линейная модель, аппроксимирующая временной ряд территориального индекса ВРП:
ИВРП = 84,46 + 4,19 t1, (5.51)
где t1 – временная переменная, определяемая соотношением
t1 = год – 2004. (5.52)
В этой модели параметр b0=84,46 есть среднее значение территориального индекса ВРП в период 2000-2008 гг., а параметр b1=4,19 – это МНК-оценка среднегодового прироста показателя (размерность обоих параметров – проценты). Характеристики качества модели (5.51) удовлетворительные: она объясняет 94,9% общей дисперсии, критерий Фишера, равный 130,5, статистически значим на уровне не хуже 0,0005. Параметры модели не только позволяют оценить место Московской области в ряду других субъектов РФ, но и свидетельствует об устойчивом развитии данного региона с ежегодным приростом индекса ВРП 4,19%.
Таблица 5.10
Параметры и критерии качества линейных моделей динамики территориального индекса ВРП в 2000-2008 гг.
|
Регион |
Код |
МНК-оценки параметров |
Критерии качества | |||
|
средний уровень показателя, % |
среднегодовой прирост, % |
коэффициент детерминации |
критерий Фишера |
уровень значимости (р-уровень) | ||
|
Белгородская обл. |
1 |
74,167 |
2,0611 |
0,733 |
19,19 |
0,003 |
|
Брянская обл. |
2 |
41,344 |
-0,6663 |
0,613 |
11,10 |
0,013 |
|
Владимирская обл. |
3 |
51,659 |
-0,6915 |
0,438 |
5,46 |
0,052 |
|
Воронежская обл. |
4 |
51,147 |
-0,5426 |
0,131 |
1,06 |
0,338 |
|
Ивановская обл. |
5 |
35,594 |
-0,7010 |
0,464 |
6,07 |
0,043 |
|
Калужская обл. |
6 |
58,487 |
-0,1002 |
0,007 |
0,05 |
0,832 |
|
Костромская обл. |
7 |
52,873 |
-1,4814 |
0,823 |
32,59 |
0,001 |
|
Курская обл. |
8 |
59,421 |
-0,3244 |
0,103 |
0,80 |
0,400 |
|
Липецкая обл. |
9 |
98,196 |
-0,1230 |
0,001 |
0,01 |
0,935 |
|
Московская обл. |
10 |
84,460 |
4,1905 |
0,949 |
130,53 |
0,000 |
|
Орловская обл. |
11 |
56,973 |
-2,7384 |
0,795 |
27,08 |
0,001 |
|
Рязанская обл. |
12 |
57,919 |
-0,8280 |
0,314 |
3,21 |
0,116 |
|
Смоленская обл. |
13 |
57,789 |
-2,5828 |
0,850 |
39,54 |
0,000 |
|
Тамбовская обл. |
14 |
49,216 |
-0,7912 |
0,353 |
3,82 |
0,091 |
|
Тверская обл. |
15 |
59,784 |
-0,5288 |
0,210 |
1,86 |
0,215 |
|
Тульская обл. |
16 |
59,213 |
-0,6057 |
0,269 |
2,57 |
0,153 |
|
Ярославская обл. |
17 |
80,438 |
-2,0535 |
0,433 |
5,36 |
0,054 |
|
Москва |
18 |
300,102 |
7,1743 |
0,730 |
18,88 |
0,003 |
|
ЦФО |
100 |
129,922 |
2,9573 |
0,917 |
77,48 |
0,000 |
Приведенные в табл. 5.10 данные получены с помощью процедуры Curve Estimation пакета статистических программ SPSS Base. Преимущество расчета с помощью этой процедуры в том, что, помимо МНК-оценок параметров линейных моделей, мы получаем характеристики их качества.
Поясним последнее. Для Московской области получена следующая линейная модель, аппроксимирующая временной ряд территориального индекса ВРП:
ИВРП = 84,46 + 4,19 t1, (5.51)
где t1 – временная переменная, определяемая соотношением
t1 = год – 2004. (5.52)
В этой модели параметр b0=84,46 есть среднее значение территориального индекса ВРП в период 2000-2008 гг., а параметр b1=4,19 – это МНК-оценка среднегодового прироста показателя (размерность обоих параметров – проценты). Характеристики качества модели (5.51) удовлетворительные: она объясняет 94,9% общей дисперсии, критерий Фишера, равный 130,5, статистически значим на уровне не хуже 0,0005. Параметры модели не только позволяют оценить место Московской области в ряду других субъектов РФ, но и свидетельствует об устойчивом развитии данного региона с ежегодным приростом индекса ВРП 4,19%.
Линейная модель, аппроксимирующая временной ряд территориального индекса ВРП для Курской области
ИВРП = 59,42 – 0,12 t1, (5.53)
имеет значительно худшие характеристики качества: она объясняет всего лишь 0,1% общей дисперсии, критерий Фишера, равный 0,8, статистически незначим (р-уровень, равный 0,400, превышает критическое значение 0,05). Таким образом, модель (5.53) неадекватна. Но ее параметры можно интерпретировать в рамках анализа временных рядов, принятого в теории статистики: параметр b0=59,42% есть среднее значение территориального индекса ВРП в период 2000-2008 гг., а параметр b1=-0,32% – это среднегодовой прирост показателя. Таким образом, полученные результаты позволяет оценить место Курской области в ряду других субъектов РФ, а факт неадекватности линейной модели свидетельствует о неустойчивости развития данного региона.
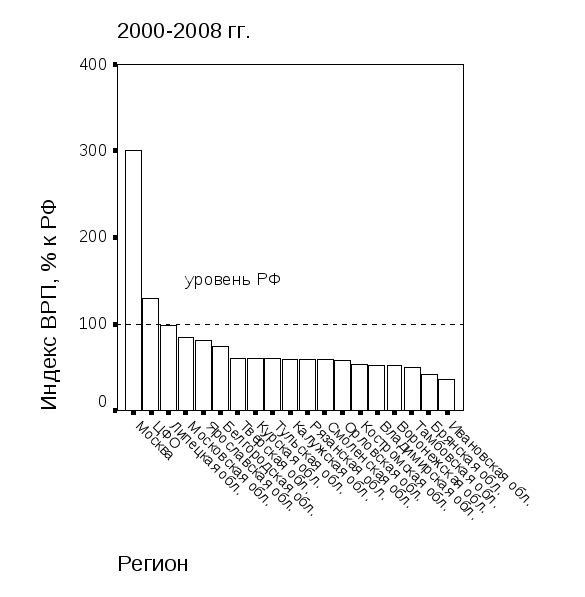
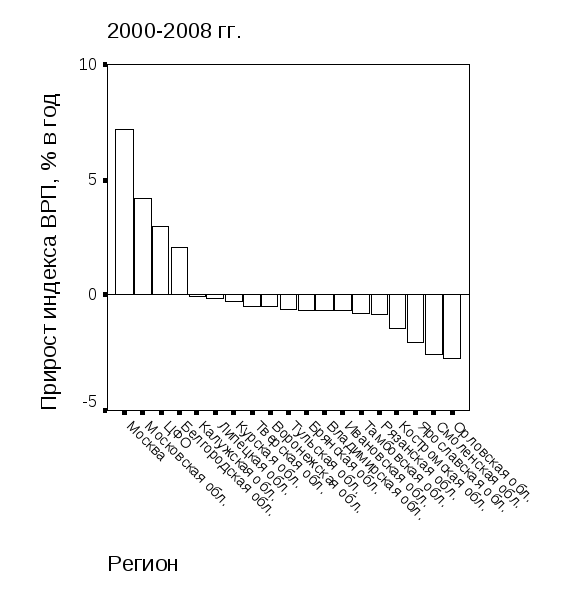
Представление о ранжировании регионов ЦФО по значениям средних показателей рядов динамики территориальных индексов ВРП дает рис. 5.44.
Из диаграммы на рис. 5.44 а следует, что г. Москва, которая характеризуется средним уровнем индекса ВРП 300%, является «выбросом», и данные по Москве необходимо исключить из дальнейшего анализа. После исключения г. Москвы из выборки регионов ЦФО проверка распределений средних показателей временных рядов по критерию Колмогорова-Смирнова показала отсутствие статистически значимых отклонений от нормального закона.
|
а |
б |
|
|
|
|
Рис. 5.44. Ранжирование регионов ЦФОпо значениям средних показателей рядов динамики территориальных индексов ВРП: а – среднее значение индекса в 2000-2008 гг.; б – среднегодовой прирост индекса ВРП | |
Заключительный этап статистических исследований территориальных индексов ВРП – проверка средних показателей временных рядов по однородной выборке регионов ЦФО на коррелированность. Эта проверка проводится с целью исключения дублирования индикаторов в случае их взаимосвязи.
На рис. 5.45 представлены две диаграммы рассеяния – одна для средних показателей временных рядов территориальных индексов ВРП, вторая – для z-преобразованных значений (z-преобразование сводится к центрированию показателей к среднему значению с последующим нормированием на среднее квадратическое отклонение [26]).
Из диаграммы рис. 5.45 а следует, что статистически значимая корреляция между средними показателями временных рядов территориальных индексов ВРП отсутствует, и на этом основании в множестве индикаторов, определяющих производственный потенциал регионов ЦФО, сохраняем оба показателя.
Диаграмма на рис. 5.45 б иллюстрирует размещение регионов ЦФО относительно средних значений индексов по однородной выборке (числа над метками соответствуют кодам регионов в табл. 5.10): регионы центральной тенденции – это Калужская (метка 6), Курская (метка 8), Рязанская (метка 12), Тверская (метка 15) и Тульская (метка 16) области. В этих регионах значения индекса ВРП – порядка 60% от среднероссийского уровня, прирост индекса ВРП близок к нулевому.
|
а |
б |
|
|
|
|
Рис. 5.45. Распределение регионов ЦФО: а – по значениям средних показателей рядов динамики территориальных индексов ВРП в 2000-2008 гг.; б – по их z-преобразованным значениям | |
На диаграмме рис. 5.45 б выделяются Московская область (метка 10) с наилучшими значениями уровня и прироста индекса ВРП, Липецкая (метка 9), Белгородская (метка 1) и Ярославская (метка 17) области. Липецкая область – единственный (кроме г. Москвы) регион ЦФО, в котором индекс ВРП близок к среднероссийскому уровню, Белгородская область характеризуется относительно высокими средними значениями уровня и прироста индекса ВРП, Ярославская область, наряду с относительно высоким средним уровнем индекса ВРП, характеризуется отрицательным значением его прироста.
Из остальных регионов следует указать Ивановскую область (метка 5), которая является аутсайдером по среднему уровню индекса ВРП – всего 35,6% от среднероссийского значения, а также Орловскую и Смоленскую области (метки 11 и 13 соответственно), которые характеризуются отрицательной динамикой индекса ВРП.
Из приведенных примеров следует, что замена пространственно-временных данных набором параметров эконометрических моделей, аппроксимирующих соответствующие временные ряды, в ряде случаев приводит к получению новых знаний об исследуемых процессах.