5.2. Прогнозирование во временных рядах

Выявление тенденций развития процессов в любой отрасли знаний практически всегда влечет за собой разработку прогноза на ближайшую перспективу. В этой связи важно подобрать ту модель, которая обеспечила бы наиболее вероятный прогноз. Далеко не всегда наиболее точная модель обеспечит наилучший прогноз. Приведем пример: в работе [149] для аппроксимации динамики изменения численности наемных работников в период 2005-2020 гг. использован кубический полином вида

Y = b₀ + b₁t + b₂t² + b₃t³, (5.25)

где Y – показатель, b₀, b₁, b₂ и b₃ – параметры модели, t – временная переменная, с вполне удовлетворительными характеристиками качества – коэффициент детерминации R²=0,998, стандартная ошибка аппроксимации StErr=0,059.

В качестве еще одного преимущества полиномиальных моделей в этой работе отмечалась то, что, например, кубический полином в ряде случаях может обеспечить общность описания динамики изменения тех или иных показателей: в квадратичной модели b₃=0, а в линейной – b₂=b₃=0.

В то же время, даже квадратичный и кубический полиномы обладают тем существенным недостатком, что их параметры не могут быть интерпретированы в экономической терминологии. Авторы цитированной выше работы отмечают, что «предпринимаемые некоторыми исследователями попытки представить коэффициент полиномиальной модели при первой степени временной переменной как «скорость» нарастания показателя, а коэффициент при второй степени временной переменной как «ускорение», вряд ли можно обсуждать всерьез» [149].

Это высказывание имеет определенное обоснование, хотя при разумном выборе временной переменной критикуемая интерпретация квадратичной модели представляется возможной. Так, если временная переменная t определяется формулой

t = год – t₀, (5.26)

где t₀ – год начала рассматриваемого временного периода, то в результате дифференцирования модели

Y = b₀ + b₁t + b₂t² (5.27)

мы получаем линейную модель роста показателя Y

dY/dt = 2b₁ + b₂t. (5.28)

Полагая t=0, из (5.27) имеем Y(0)=b₀, т.е. коэффициент b₀ может быть интерпретирован как расчетное значение показателя в начальный момент времени. Аналогично, из (5.28) при t=0 получаем dY/dt(0)=2b₁, т.е. коэффициент b₁ можно интерпретировать как «скорость» нарастания показателя. Продолжая формальную операцию дифференцирования, получаем модель постоянства «ускорения» нарастания показателя Y:

d²Y/dt² = b₂. (5.29)

С формальной точки зрения, здесь все верно, и параметр b₁ в данном случае можно интерпретировать как «скорость» нарастания показателя, а параметр b₂ как «ускорение», однако остается не ясным, как интерпретировать параметры модели b₁ и b₂ в содержательных терминах.

Есть и другая причина, по которой не следует применять полиномиальные модели в целях прогнозирования, особенно по коротким временным рядам – это изменение характера тренда, аппроксимируемого кубическим и даже квадратичным полиномом, на разных участках парабол.

Приведем конкретный пример. В работе [166] на примере анализа динамики некоторых целевых переменных немецкой макроэкономики показано, что в математическом плане эти временные ряды достаточно хорошо аппроксимируются полиномами – квадратичными и кубическими функциями, но они абсолютно непригодны для решения задач прогнозирования в случае относительно коротких временных рядов. Этот вывод в цитированной работе подтверждается графиками, представленными на рис. 5.8 и 5.9.

Рис. 5.8. Динамика и аппроксимация показателей экономики Германии «чистое кредитование» в период 1984-1989 гг. квадратичным полиномом

Действительно, как следует из графика рис. 5.8, динамика изменения объема чистого кредитования вполне удовлетворительно аппроксимируется квадратичным полиномом (скорректированный коэффициент детерминации R²=0,9391, величина критерия Фишера F=39,6 отвечает высокому статистическому уровню 0,007).

Кубический полином (рис. 5.9) обеспечивает еще более точное приближение к эмпирическим данным: скорректированный коэффициент детерминации R²=0,9998, а величина критерия Фишера составляет F=7832,5, что отвечает статистическому уровню 0,0001.

Однако аппроксимация и квадратичной параболой, и кубической функцией не обеспечивает «разумного», с точки зрения экономики, прогноза. В случае аппроксимации эмпирических данных по динамике объема чистого кредитования на ближайшие два года прогнозируется ускоренное снижение показателя, что противоречит интуиции, подсказывающей, что темпы снижения объема чистого кредитования вряд ли могут измениться столь радикально. Еще более неубедителен прогноз по кубической параболе – в этом случае на ближайший год планируется некоторое уменьшение показателя, но затем его существенный рост, что никак не вытекает из реальных временных изменений объема чистого кредитования (графики на рис. 5.8 и 5.9).

Автор цитируемой работы (и мы согласны с ним) заключает: «если цель аппроксимации эмпирических временных рядов – прогнозирование, не следует стремиться к высокой точности аппроксимирующей модели; гораздо важнее добиваться лучшего приближения к последним уровням рядов, при «разумной» экономической интерпретации модели» [166].

Рис. 5.9. Динамика и аппроксимация показателей экономики Германии «чистое кредитование» в период 1984-1989 гг. кубическим полиномом

Итак, область применения полиномиальных моделей – интерполяция, и здесь вполне закономерно использовать и квадратичные, и кубические полиномы, но не экстраполяция, особенно, если речь идет о прогнозировании по довольно коротким временным рядам. Но возникает вопрос – какие модели временных рядов следует применять в целях прогнозирования? Ведь одни и те же эмпирические данные могут быть описаны не одной, а несколькими конкурирующими моделями. Нам представляется, что здесь следует руководствоваться общим принципом – рациональной является та модель, которая имеет минимально возможное число параметров, которые поддаются четкой экономической интерпретации. При этом надо учитывать реальные возможности «перебора» альтернативных моделей, предоставляемые современными пакетами анализа данных, в том числе процедурой «оценка кривой» пакета SPSS Base.

Наиболее простая модель тренда временного ряда – линейная модель. Пример такой модели для динамики заболеваемости населения РФ в целом приведен на рис. 5.10 а.

а	б
Рисунок 5.10 – Динамика заболеваемости населения РФ в 2000-2010 гг. (а) и прогнозирования показателя на перспективу (б)

Из рис. 5.10 а следует, что данный ряд динамики характеризуется линейным нарастающим трендом. В результате регрессионного анализа выявлено, что он может быть описан моделью:

Y = 716,09 + 6,69 t; (5.30)

где t – временная переменная (годы), определяемая соотношением

t = год – 2000. (5.31)

Модель (5.30) объясняет 85,5% общей дисперсии, критерий Фишера F=53,08 статистически значим на уровне не ниже чем 0,00005. Это позволяет интерпретировать ее параметры следующим образом: в среднем прирост заболеваемости населения РФ составляет 6,69 промилле в год. Свободный коэффициент регрессии b₀=716,09 интерпретируется как расчетное значение заболеваемости населения РФ в начальный год наблюдаемого периода, т.е. в 2000 г.

Поскольку качество полученной модели высокое, можно использовать ее для прогноза (рис. 5.10 б). Согласно прогнозу, заболеваемость населения РФ в 2012 г. повысится до 803,1 промилле с доверительным 90%-м интервалом 781…825 промилле.

Модель (5.30) при принятом нами назначении временной переменной имеет то преимущество, что параметр b₀ подлежит верификации, т.е. его можно сравнить с фактическим значением заболеваемости населения. Так, из графика рис. 5.10 б видно, что расчетное значение изучаемого показателя достаточно близко к фактическому значению заболеваемости населения в 2000 г.

Напомним, что в общей теории статистики оценку коэффициента линейной регрессии дает средний абсолютный прирост показателя, а другая характеристика ряда динамики – средний уровень ряда – дает оценку параметра b₀ при условии, что временная переменная t определяется соотношением

t = год – середина интервала времени. (5.32)

Понятно, что оценка параметров линейного тренда методом наименьших квадратов (МНК) – предпочтительнее.

В общей теории статистики, помимо линейной, применяется еще две модели – модель экспоненциального роста и параболическая модель. Параболическую модель мы рассматривали выше (это квадратичный полином), поэтому остановимся на модели экспоненциального роста.

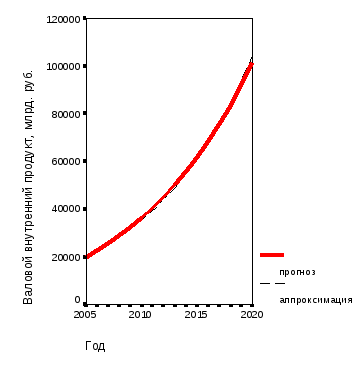
Модель экспоненциального роста широко распространена постольку, поскольку она отвечает общему закону природы и общества: прирост большинства показателей пропорционален достигнутому уровню и интервалу времени; классическим примером является известный закон Мальтуса роста населения. Не являются исключением и показатели социально-экономического роста. Так, в работе [149] характер экспоненциального роста носит динамика сразу двух показателей – валового внутреннего продукта (ВВП) и фонда оплаты труда (ФОТ) – рис. 5.11.

а	б
Рис. 5.11. Динамика изменения значений прогнозных показателей социально-экономического развития РФ: а – валовой внутренний продукт, б – фонд оплаты труда

Авторами этой работы в результате реализации процедуры «подгонка кривых» пакета анализа данных общественных наук SPSS Base установлено, что оба ряда могут быть с высокой точностью аппроксимированы экспонентами вида

Y_i = b₀ exp(b₁t), (5.33)

где Y_i – показатель, b₀ и b₁ – параметры модели, t – временная переменная, которая в цитируемой статье «отсчитывалась» от 2004 года. Экономический смысл параметров модели следующий: параметр b₀ – это расчетная величина показателя при значении временной переменной t=0 (в данном случае, в 2004 году, предшествовавшем интервалу прогноза), а параметр b₁ – это коэффициент среднегодового прироста показателя. В случае динамики ВВП параметр b₁=0,108. Это означает, что согласно прогнозу, валовой внутренний продукт в период 2005-2020 гг. будет увеличиваться со среднегодовым темпом роста 110,8%, а для фонда оплаты труда прогнозируются немногим большие среднегодовые темпы роста – 111,1%. Обе экспоненциальные модели характеризуются высокими показателями качества: значения коэффициента детерминации составляют 0,998 и 0,994 для ВВП и ФОТ, соответственно.

Экспоненциальному закону «подчиняется» также динамика роста среднемесячной заработанной платы, причем параметр b₁=0,116, т.е. в соответствии с прогнозом, этот показатель в период 2005-2020 гг. будет увеличиваться со среднегодовым темпом роста 111,6% – быстрее, чем фонд оплаты труда. Эта экспоненциальная модель также характеризуется высокими показателями качества: значение коэффициента детерминации составляет 0,996.

Некоторым недостатком приведенных выше экспоненциальных моделей является то, что параметр b₀ при принятой в работе [149] временной переменной не подлежит прямой верификации. Однако и здесь, как мы поступили в случае линейной модели, можно «сместить» начальное значение временной переменной на год позже (т.е. положить t=0 для начала интервалу прогноза), и тогда параметр b₀ можно верифицировать.

Обратим внимание, что экспоненциальная модель – это модель ускоренного роста показателя. В общей теории статистики она носит название модели постоянства темпа роста, тогда как линейная модель – это модель постоянства абсолютного прироста. А когда рост показателя со временем замедляется, применяется другая – степенная модель положительной динамики. Классическим примером является модель предельной склонности к потреблению вида

M = α D^β, (5.34)

где M – уровень потребления, D – доход, α и β – параметры модели. Экономический смысл параметра β – коэффициент эластичности, который в данном случае меньше единицы; он показывает, на сколько процентов изменится потребление при изменении дохода на 1 процент. То, что β<1, отражает, что предельная склонность к потреблению монотонно убывает с ростом. Если говорить о степенной модели динамики вида

Y = b₀ t ^b1, (5.35)

то интерпретация коэффициента b₁ как коэффициента эластичности некорректна, тем не менее, по его величине можно судить о степени замедления роста показателя.

На рис. 5.12 представлены ряды динамики одного из основных макроэкономических показателей – уровня экономической активности населения двух федеральных округов – Центрального и Сибирского ФО (для наглядности обе диаграммы имеют одинаковый масштаб; с этой же целью на диаграммах показан уровень экономической активности населения РФ в 2010 г. 67,7%). Видно, что если в ЦФО экономическая активность населения уже в 2007 г. превзошла среднероссийский уровень 2010 г., то в СФО этот уровень так и не был достигнут. Возникает вопрос – а что можно ожидать в последующие годы, при сохранении наметившейся тенденции?

а	б
Рис. 5.12. Аппроксимация динамики экономической активности населения в период 2001-2010 гг. степенной функцией и прогноз на 2011-2013 гг.: а – ЦФО; б – СФО. Пунктирная прямая – уровень РФ в 2010 г.

Судя по характеру изменения данного показателя во времени – рост с насыщением, – можно предположить наличие степенного тренда динамики уровень экономической активности населения в обоих федеральных округах. Выполненный нами статистический анализ подтвердил эту гипотезу: временные ряды и по ЦФО, и по СФО вполне удовлетворительно аппроксимируются степенными функциями, в обоих случаях коэффициент детерминации превысил значение 0,8 (R²=0,871 и 0,9 для данных по ЦФО и СФО, соответственно).

На этом же рисунке показаны результаты прогноза уровня экономической активности населения в рассматриваемых федеральных округах: согласно наиболее вероятному прогнозу (степенная функция на рис. 5.12), экономическая активность населения Сибирского ФО не достигнет уровня РФ 2010 года и в 2013 году.

Вернемся к модели (5.35). Очевидно, что при t=1 из (5.35) вытекает: Y(t=1)=b₀, т.е. свободный коэффициент степенной модели интерпретируется как расчетная величина показателя при значении временной переменной t=1. В рассматриваемом случае значение временной переменной t=1 соответствует начальному году интервала прогноза, и, сравнивая величину параметра b₀ с эмпирическими данными, можно выполнить верификацию степенной модели тренда. Как уже отмечалось выше, по величине параметра b₁ можно судить о степени замедления роста показателя. Для ЦФО b₁=0,0249, для СФО b₁=0,0279, т.е. «насыщение» уровня экономической активности населения в СФО происходит быстрее.

Со степенной моделью тренда конкурирует модель гиперболического тренда, аналитически выражаемая формулой

Y = b₀ + b₁ / t . (5.36)

Здесь, как и в модели (5.34), временная переменная не может быть равна нулю.

Модель гиперболического тренда (5.36) принципиально отличается от степенной модели (5.35): если рост показателя, аппроксимируемый степенным трендом, не ограничен, то согласно модели (5.36), он ограничен «сверху» (при условии b₁<0; случай b₁>0 отвечает ниспадающему тренду), и этот предел равен параметру b₀. Смысловую интерпретацию имеет и другой параметр гиперболической модели – b₁ – его отрицательное значение равно предельному расчетному приросту показателя. Соответственно, сумма параметров b₀+b₁ дает предельное расчетное значение показателя (здесь параметр b₁ берется со своим знаком).

Из хода графика временного ряда уровня экономической активности населения в ЦФО видно, что гиперболическая модель не обеспечит высокого качества аппроксимации. В отличие от этого, можно рассчитывать на более высокое качество аппроксимации гиперболической моделью уровня экономической активности населения в СФО.

Действительно, как следует из сравнения графиков рис. 5.13, гиперболический тренд заметно хуже описывает динамику уровня экономической активности населения в ЦФО и лучше – в СФО.

а	б
Рис. 5.13. Аппроксимация динамики экономической активности населения в период 2001-2010 гг. гиперболической функцией и прогноз на 2011-2013 гг.: а – ЦФО; б – СФО. Пунктирная прямая – уровень РФ в 2010 г., штрихпунктирная прямая – предельное значение показателя

На рис. 5.13 штрихпунктирными прямыми обозначены предельные значения уровня экономической активности населения в ЦФО и СФО. Для СФО это значение равно 66,38%, т.е., согласно гиперболической модели, экономическая активность населения СФО не достигнет уровня РФ 2010 г. не только в 2013 г., но и в дальнейшем.

О худшем качестве гиперболических моделей свидетельствует и сравнение таких показателей качества аппроксимации, как коэффициент детерминации и критерий Фишера (табл. 5.5).

Приведем гиперболические модели тренда динамики уровня экономической активности населения в рассматриваемых федеральных округах в явном виде:

для ЦФО

Y (ЦФО) = 68,1 – 3,73 / t , (5.37)

для СФО

Y (СФО) = 63,38 – 4,34 / t , (5.38)

где t – временная переменная (годы), определяемая соотношением

t = год – 2000. (5.39)

Сравнивая значения параметра b₁ в моделях (5.36) и (5.37), можно заключить, что в целом уровень экономической активности населения СФО ниже, чем в ЦФО, но при этом в СФО этот показатель в рассматриваемый период развивался динамичнее.

Таблица 5.5

Показатели качества аппроксимации динамики экономической активности населения

Федеральный округ	Показатель качества модели	Модель
		степенная	гиперболическая
Центральный ФО	Коэф. детерминации	0,871	0,624
	Критерий Фишера	54,1	13,3
Сибирский ФО	Коэф. детерминации	0,900	0,738
	Критерий Фишера	72,2	22,6

Рассмотрим теперь применение гиперболической функции для экстраполяции ниспадающего тренда. Именно таким трендом характеризуется динамика изменения численности безработных в период 2003-2006 гг. в Центральном и Сибирском федеральных округах – рис. 5.14.

Из диаграммы на рис. 5.14 а видно, что динамика уменьшения численности безработных в ЦФО характеризуется линейным трендом, а в СФО – трендом с «насыщением», т.е. в случае СФО этот тренд вполне может быть аппроксимирован гиперболической функцией.

Рис. 5.14 б подтверждает это предположение: расчетные значения достаточно хорошо совпадают со статистикой, и доверительные интервалы, построенные нами на уровне 90%-й надежности, не столь велики. Модель тренда динамика уменьшения численности безработных в СФО выражается следующей формулой:

Y (СФО) = 830,82 + 328,18 / t , (5.40)

где t – временная переменная (годы), определяемая соотношением

t = год – 2002. (5.41)

а	б
Рис. 5.14. Динамика численности безработных в ЦФО и СФО в период 2003-2006 гг. (а) и аппроксимация динамики численности безработных в СФО гиперболической функцией и прогноз на 2007-2009 гг. (б). Пунктирная прямая – предельное значение показателя

Согласно модели (5.40), предельное значение численности безработных в СФО составляет 830,82 тыс. человек, при расчетном начальном уровне 830,82+328,18=1159,00 тыс. человек. Эта значение достаточно близко к наблюдаемой численности безработных в СФО в 2003 г. – 1156 тыс. человек, что также говорит о неплохой точности аппроксимации эмпирических данных.

Представленные выше результаты убеждают, что из многообразия моделей динамики социально-экономических показателей в прогностических целях целесообразно использовать такие двухпараметрические функции, как линейная, экспоненциальная, степенная и гиперболическая. Полиномиальные функции могут быть использованы только в интерполяционных целях, поскольку применение для экстраполяции полиномов даже низкой степени – кубических и квадратичных зачастую значительно искажает прогноз, особенно в случае коротких временных рядов.