Глава 2. Одномерные процедурыАнализа данных в управлении

2.1. Проверка выборочных данных на соответствие требованиям статистического анализа

Важнейшим условием корректности многих процедур статистического анализа является соответствие выборочных данных ряду требований. Первое, и основное требование – данные должны быть измерены в интервальной, относительной или абсолютной шкалах. К сожалению, часто исследователи производят математические операции над данными, измеренными в порядковой шкале (наиболее типичный пример – в балльной шкале), – это, как минимум, некорректно.

Второе требование – выборка должна быть однородной, не содержать «выбросов», т.е. экстремальных значений. Проверка на соблюдение выборочных данных этому требованию проводится путем построения ящичковых диаграмм (диаграмм Тьюки).

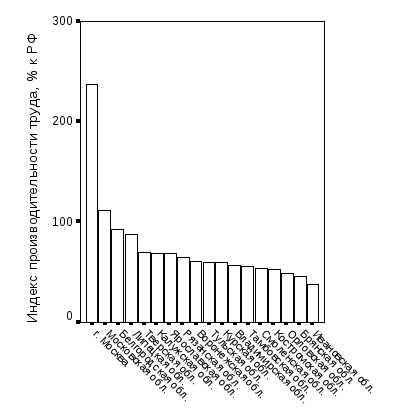
Приведем пример. Одним из важнейших индикаторов социально-экономического развития регионов является индекс производительности труда, рассчитываемый как отношение валового регионального продукта (ВРП) к численности занятых в экономике в данном регионе к аналогичному показателю по всем субъектам Российской Федерации. По данным за 2009 г., этот индекс по регионам Центрального федерального округа варьировал в пределах от 37,10% (Ивановская область) до 236,42% (г. Москва), так что размах составлял 6,37 крат. Таким образом, налицо значительная асимметрия данного индикатора социально-экономического развития. Графически эта асимметрия может быть наглядно представлена в виде ящичковой диаграммы – рис. 2.1 а.

Поясним элементы диаграммы, представленной на рис. 2.1 а. Звездочкой на ней отмечено экстремально большое значение территориального индекса производительности труда в Москве, а кружочком – повышенное значения данного индикатора в Московской области. На первый взгляд, эти два региона необходимо исключить из выборки, но возникает вопрос – а что же тогда будет представлять из себя такая «усеченная» выборка объемом всего 16 регионов? Если проанализировать диаграмму Парето, приведенную на рис. 2.1 б, то можно заметить, что только Москва сильно отличается от остальных регионов по индексу производительности труда. На этом основании из полной выборки регионов ЦФО исключаем только Москву.

а	б
Рис. 2.1. Распределение по регионам ЦФО территориального индекса производительности труда в 2009 г.: а – ящичковая диаграмма; б – диаграмма Парето

Ящичковая диаграмма для распределения территориального индекса производительности труда по регионам усеченной таким образом выборки регионов ЦФО представлена на рис. 2.2 а.

а	б
Рис. 2.2. Распределение по усеченной выборке регионов ЦФО (без Москвы) территориального индекса производительности труда в 2009 г.: а – ящичковая диаграмма; б – диаграмма Парето

Естественно, на ящичковой диаграмме по-прежнему отмечаются повышенные значения территориального индекса производительности труда в Московской и Белгородской областях. Но здесь необходимо учесть еще одно требование к выборочным данным – требование соответствия распределения изучаемого показателя нормальному закону. Сравнивая эмпирическую гистограмму, приведенную на рис. 2.2 б, с теоретической кривой нормального распределения, можно предположить, что путем логарифмического преобразования территориального индекса производительности труда можно добиться соблюдения и этого требования к выборочным данным. (Заметим, что логарифмическое преобразование довольно часто приходится использовать в случае правосторонней асимметрии социально-экономических показателей.)

Действительно, как следует из диаграмм, приведенных на рис. 2.3, логарифмическое преобразование территориального индекса производительности труда приводит к симметризации распределения исходного показателя. Правда, при этом теряется наглядность, но, как будет показано в дальнейшем, использование в анализе вместо исходных показателей их логарифмов имеет и свои преимущества.

а	б
Рис. 2.3. Распределение по усеченной выборке регионов ЦФО (без Москвы) логарифма территориального индекса производительности труда в 2009 г.: а – диаграмма Парето; б – ящичковая диаграмма

При всех достоинствах графического представления результатов анализа необходимо обращаться и к аналитическим процедурам. В данном случае речь идет об использовании непараметрического критерия Колмогорова-Смирнова, предусмотренного в пакете SPSS Base. Его преимущество перед графическими методами проверки на нормальность распределения в том, что с помощью критерия Колмогорова-Смирнова можно дать статистическую оценку надежности принимаемого решения о соответствии показателя нормальному распределению.

В табл. 2.1 приведены результаты такой проверки для двух показателей – исходного территориального индекса производительности труда в 2009 г. и логарифма его значений.

Таблица 2.1

Применение непараметрического критерия Колмогорова-Смирнова для проверки на нормальность распределения

	Статистика	Индекс производительности труда, % к РФ		Логарифм индекса производительности труда
	Объем выборки	17		17
Параметры нормального распределения	Среднее	64,0341		4,1239
	Стандартное отклонение	18,50941		0,26984
Наибольшая разность	Абсолютная	0,201		0,150
	Положительная	0,201		0,150
	Отрицательная	-0,101		-0,089
Критерий Колмогорова-Смирнова Z			0,831		0,617
Асимптотическая значимость (двусторонняя)			0,495		0,841

Поясним элементы табл. 2.1. Для нас важны две последние строки этой таблицы, в которых приведены значения критерия Колмогорова-Смирнова Z и асимптотическая значимость. Видно, что критерий Колмогорова-Смирнова Z для исходного показателя (0,831) больше, чем для его логарифма (0,617), тогда как асимптотическая значимость – меньше – 0,495 против 0,841. Смысл асимптотической значимости – вероятность принятия решения о соответствии распределения нормальному. Для исходного показателя эта вероятность равна 0,495, а для логарифмически преобразованного показателя она заметно больше и составляет 0,841, т.е. приближается к 100%. Отсюда следует, что в дальнейшем анализе лучше использовать логарифмы значений территориального индекса производительности труда.