§9.2.Функции и отображения. Предел, непрерывность

9.2.1. Функции и отображения

Определение. Функция сопоставляет элементам множества ( называемого областью определения) числа .

Определение. Отображение сопоставляет элементам множества элементы.

Таким образом, функция – это частный случай отображения . Задать отображение – это все равно, что задатьфункций

Примеры.

1. - функция двух переменных, паре сопоставляет число.

2. Отображение

3. Вектор-функция Винтовая линия.

4. Последовательность 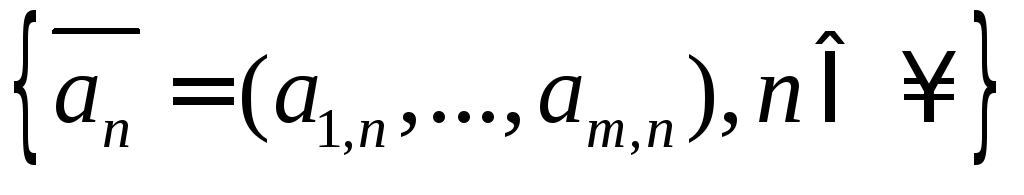представляет собой отображение .

9.2.2. Предел, непрерывность функции и отображения

Пусть - предельная точка области определения .

Определение. Пределом отображения при стремленииназывается элемент ,удовлетворяющий условию

Для предела отображения используется обычное обозначение

Рассматривая симметричные окрестности, перепишем это определение в метрических пространствах следующим образом

,

или

выполняется неравенство

Или, вспоминая определение (2) расстояния,

выполняется неравенство

Теорема 9.4. .

►Поскольку , выполняются неравенствапри. Но это как раз и означает, что.

. Пусть - фиксировано. Выберемтак, чтобы привыполнялось неравенствоВзявполучаем, что привыполняется неравенство.◄

Определение. Отображение непрерывно в точке , если

Согласно сказанному выше, непрерывность отображения равносильна непрерывности всех функций.

Так же, как и в случае функций одной переменной, справедлива следующая теорема.

Теорема 9.5. Если , то,, и если, то.

Замечание. Как и в одномерном случае, при предельном переходе для функций нескольких переменных сохраняется нестрогое неравенство. Точно также сохраняется теорема о «зажатой» переменной.

Следствие. Сумма, разность, произведение и частное ( при ) непрерывных функцийиявляются непрерывными функциями.

Теорема 9.6. Если непрерывно в точке, отображение непрерывно в точке, то отображение непрерывно в точке.

►Для всякой окрестности существуеттакая, что. Но. Эта окрестность - искомая, т.к. .◄

Теорема 9.7. (Теорема о сохранении знака непрерывной функции). Если то.

►Достаточно доказать, что если , то и. Действительно, взявполучаем по определению непрерывности окрестностьтакую что .◄

Теорема 9.10. Непрерывный образ компактного множества есть компактное множество.

Следствие. Непрерывная на компакте функция достигает на нём своего наибольшего и наименьшего значений.

В главе 5 доказан частный случай этой теоремы. Именно, из утверждений теорем 5.3 и 5.4 следует, что непрерывный образ отрезка представляет собой отрезок. Общий случай оставим без доказательства.

Определение. Прямолинейным отрезком в называется подмножество,состоящее из точек вида

.

Ломаная линия в представляет собой непрерывную кривую, составленную из конечного числа прямолинейных отрезков.

Определение. Назовём открытое множество связным, если любые две его точки можно соединить ломаной линией, целиком лежащей внутри этого множества.

Теорема 9.11. Непрерывный образ связного множества есть связное множество.

Замечание. Эта теорема обобщает теорему 5.4 о том, что непрерывный образ промежутка представляет собой числовой промежуток. Общий случай оставим без доказательства.

Теорема 9.12.(Теорема Кантора). Непрерывная на компакте функция равномерно непрерывна на нем, т.е. .