Глава 13. Условный экстремум
§13.1.Условный экстремум
13.1.1. Определение условного экстремума
Пусть дана функция
и предположим, что переменные
удовлетворяют уравнениям связи
.(1).
Определение.
В точке
,
удовлетворяющей уравнениям (1) функция
имеет условный
минимум (максимум)
если неравенство
(
)
выполняется в некоторой окрестности
точки
для всех точек
этой окрестности, удовлетворяющих
условиям (1).
13.1.2. Необходимые условия. Метод множителей Лагранжа
Для упрощения
выкладок рассмотрим случай функции
и двух уравнений связи
,
.
Предположим, что функции
обладают непрерывными частными
производными, причем ранг матрицы
равен 2. Для определенности, пусть
.
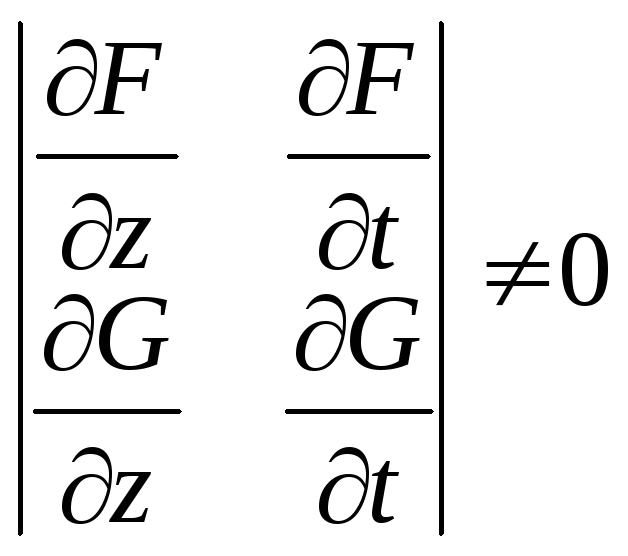Тогда по теореме о системе неявных
уравнений уравнения связи можно решить,
выразив переменные
в виде функций от
:
,
,
где
– непрерывно дифференцируемые функции
и понятие условного экстремума функции
совпадает с экстремумом функции
.
Стало быть, дифференциал этой функции
–
тождественно равная нулю функция от
,
т.е. должно выполняться условие
, равносильное тому, что
,
, (2).
иными словами,
,
.
Для нахождения
,
,
,
воспользуемся уравнениями связи
(3).
Из этой системы
можно линейно выразить
и
через
и
,
что и дает искомое выражение для
,
,
,
.
Предоставим это полезное упражнение
читателю.
Есть, однако, замечательный прием, называемый методом неопределенных множителей Лагранжа, который позволяет обойтись без нахождения решения этой системы. Изложим этот метод.
По инвариантности
формы дифференциала, условие
(или условие (2))равносильно условию
,
т.е.
(4).
Умножим уравнения
(3) на некоторые числа
и
соответственно и сложим с (4):
(5).
Выберем
и
так, чтобы коэффициенты при
и
одновременно обращались в 0. Это можно
сделать потому, что определитель системы
(6)
не равен 0.
Тогда (5) примет
вид
,
где
– дифференциалы независимых переменных.
Поэтому и
(7).
Таким образом,
необходимые условия экстремума
вспомогательной функции
совпадают с уравнениями (6) и (7) и, тем
самым, с необходимыми условиями условного
экстремума.
13.1.3. Достаточные условия экстремума. Окаймлённый гессиан
Для простоты
изложения ограничимся функцией
от двух переменных, подчиненных условию
.
Предполагаем, что функции
обладают непрерывными производными до
второго порядка включительно и обозначаем,
например,
,
,
и т.п. Для нахождения точки, в которой
возможен условный экстремум, используем
метод множителей Лагранжа, описанный
выше. Строим функцию Лагранжа
.
(отметим, что иногда
пишут
.
Никакой разницы это не даст, т.к. уравнение
равносильно уравнению
).
Точки, в которых может быть условный экстремум, удовлетворяют системе
Для того, чтобы
выяснить, есть ли экстремум в найденной
точке
(или одной из найденных точек, если
система имеет не одно решение), следует
использовать второй дифференциал, как
и в случае обычного экстремума. Однако
в рассматриваемом случае
,
откуда дифференцируя, находим:
,
или, если, например
,то
.
Кроме того, при
условии
рассматриваемая функция
просто совпадает с
и поэтому экстремумы этих функций
совпадают. Поэтому далее исследуем на
экстремум функцию
.
Найдём её второй дифференциал.
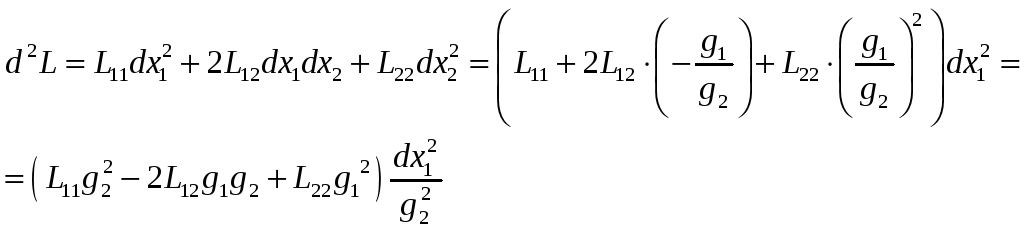
Итак, знак
(при условии что переменные
связаны уравнением
,
откуда
)
совпадает со знаком величины
(8)
Для удобства запоминания рассмотрим определитель (окаймленный гессиан) и его разложение по первой строке
(9)
Сравнивая (8) и (9) видим, что в рассматриваемой задаче знак второго дифференциала противоположен знаку окаймленного гессиана.
Поэтому если
,
то
и в точке
есть условный максимум, если
,
то
и в точке
есть условный минимум.
Замечание.
Вновь обратим внимание на то, что если
уравнение связи
можно решить, выразив, например
,
то вопрос об условном экстремуме сведется
к исследованию на экстремум обычных
функций от одной переменной.
Замечание. Вопрос о том, нет ли среди уравнений связи лишних, решается с помощью теории независимости функций ( см. приложение).