Matanaliz
.doc
Интеграл
О. Функция
называется первообразной для
если
.
О. Неопределенный
интеграл
–
множество первообразных вида
.
Таблица интегралов:
1.
; 2.
;
;
3.
;
4.
;
5.
6.
;
7.
;
8.
;
9.
.
О. Определённый
интеграл
. Геометрически – площадь криволинейной
трапеции.
Формула интегрирования
по частям:
.
№.
.
№.
.
.
.
.
№.
.
.
.
№.
.
№.
.
№.
.
№.
.
.
.
.
.
№.
.
№.
.
№.
.
№.
.
№.
.
№.
.
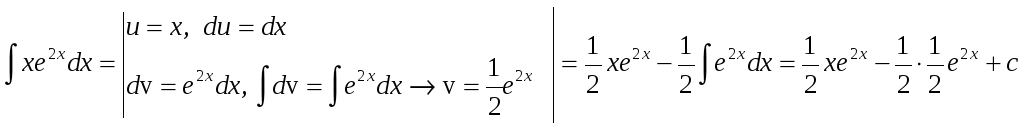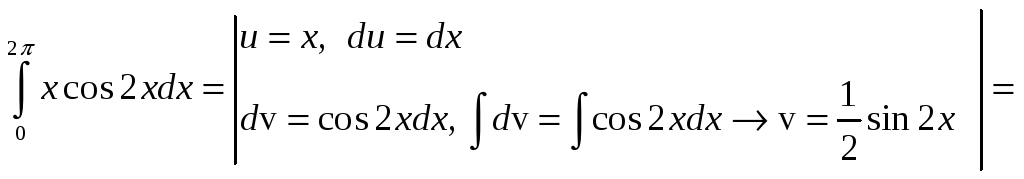
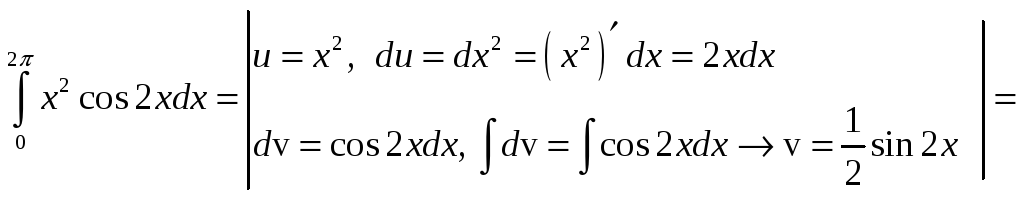
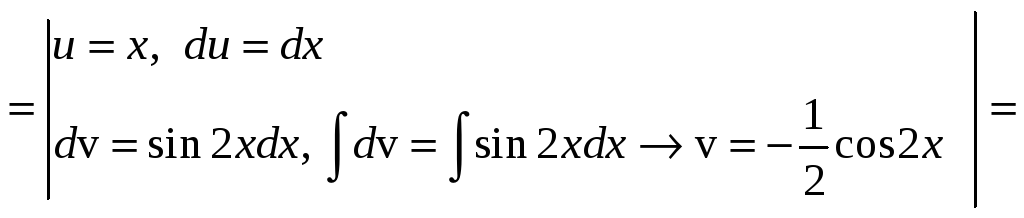
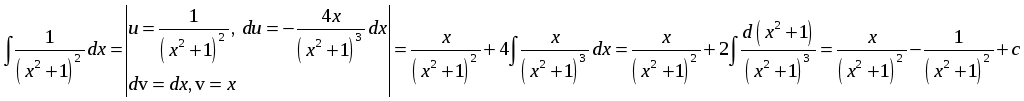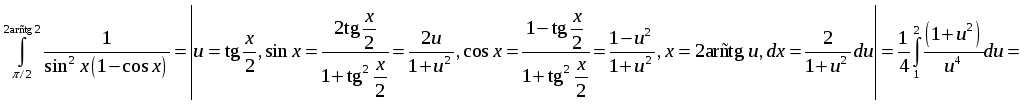
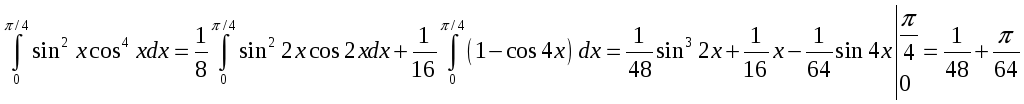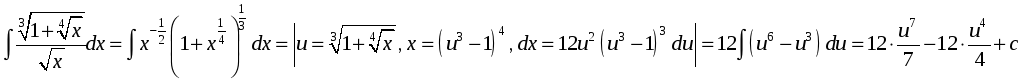№. Площадь фигуры,
ограниченной параболой
и прямой
:
1)
; 2)
.
№. Площадь фигуры:
.
.
№. Площадь фигуры:
.
.
.
№. Длина дуги
кривой:
.
.
.
№. Длина дуги
кривой:
.
.
.
.
№. Длина дуги
кривой:
.
.
.
№. Объем тела,
образованного вращением вокруг оси
прямой
,
(конус):
.
Дифференциальные уравнения
I.
При описании движения материального
объекта используются характеристики:
– перемещение,
– скорость,
– ускорение (при поступательном
движении);
– угол поворота,
– угловая скорость,
– угловое ускорение (при описании
вращений);
– время. Постановка проблемы: найти
функцию, если известна её производная.
№.
.
1) от равенства в
производных перейдём к равенству в
дифференциалах:
.
2) от равенства в
дифференциалах перейдём к равенству в
интегралах:
.
3) вычислим (общий
интеграл – решение диф.уравнения):
.
Частный случай:
. Тогда
(общее решение).
Задача с начальным
условием:
,
. Используем найденное решение:
.
Решение,
удовлетворяющее уравнению и начальному
условию
.
№.
.
1)
. 2)
.
3)
.
.
.
,
.
,
.
№.
.
1)
. 2)
.
3)
.
.
.
,
.
.
.
№.
.
1)
. 2)
.
3)
.
.
.
,
.
,
.
Простейшие типы дифференциальных уравнений
1. Уравнение с
разделёнными
переменными:
.
1) от равенства в
дифференциалах перейдём к равенству в
интегралах
.
2) вычислим (общий
интеграл – решение диф.уравнения):
.
2. Уравнение с
разделяющимися
переменными:
.
1) разделим переменные
получили уравнение
с разделёнными переменными
.
2) от равенства в
дифференциалах перейдём к равенству в
интегралах
.
3) вычислим (общий
интеграл – решение диф.уравнения):
.
3. Линейное
уравнение
первого порядка:
, где
– известны.
1) решение ищем в
виде произведения двух неизвестных
функций
. Тогда
.
Уравнение примет
вид:
или
.
2) Пусть
. Тогда
.
3) Решим первое уравнение (уравнение с разделяющимися переменными)
.
4) Решим второе
уравнение (уравнение с разделяющимися
переменными), в котором неизвестно
:
. Общее решение
линейного уравнения:
.
№.
или
. Пусть
или
.
1)
,
или
.
2) Пусть
. Тогда
.
3)
.
4)
.
.
4. Однородное
диф.уравнение второго порядка с
постоянными коэффициентами:
.
1) Составляем
характеристическое уравнение
(алгебраическое)
.
2) Случай 1.
действительные.
Общее решение однородного уравнения
.
Случай 2.
действительные.
.
Случай 3.
комплексные.
.
№.
. 1.
.
2.
.
Начальные условия:
.
.
Решение удовлетворяющее
уравнению и начальным условиям:
.
№.
. 1)
.
2)
.
№.
.
1)
.
2)
.
5. Неоднородное
уравнение второго порядка с постоянными
коэффициентами:
.
Общее решение
неоднородного уравнения есть сумма
общего решения однородного уравнения
и частного решения неоднородного
.
№.
.
Частное решение
ищем в виде
,
,
.
Общее решение
неоднородного уравнения:
.
Пусть начальные
условия:
.
Тогда:
.
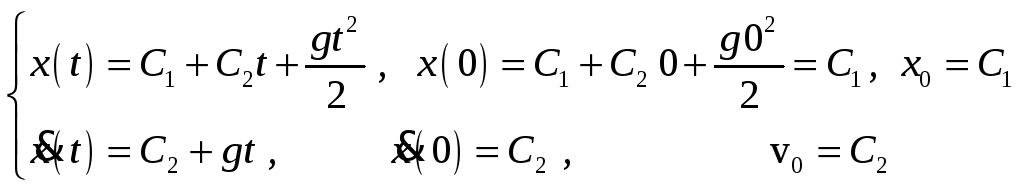Решение неоднородного
уравнения, удовлетворяющее начальным
условиям
.
Найти общий интеграл дифференциальных уравнений:
№.
.
.
№.
.
1)
.
2)
.
3)
.
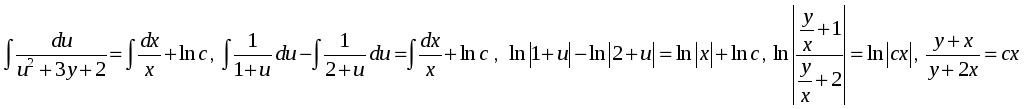Решить задачу Коши:
№.
.
1) Решение уравнения
ищем в виде:
.
Тогда
.
2) Пусть
. Тогда
. 3)
.
4)
5)
.
6)
.
Найти общие решение дифференциальных уравнений:
№.
.
1) Для однородного
уравнения
составим характеристическое
(алгебраическое)
.
2) Общее решение однородного уравнения
.
3) Частное решение
неоднородного уравнения ищем в виде:
.
Тогда:
и
уравнение примет вид:
.
Приравнивая
коэффициенты при одинаковых степенях
,
получим:
.
любой, пусть
.
4) Общее решение
неоднородного уравнения:
.
№.
. 1)
2)
.
.
Приравнивая коэффициенты при
получим:
.
3)
.
№.
.1)
.
2)
.
Приравняем коэффициенты при
:
.
3)
.
№.
. 1)
.
2)
.
3)
.4)
.
Решение линейных дифференциальных уравнений второго порядка
с постоянными коэффициентами методом Лапласа
О.
– оригинал,
(
– комплексный параметр) – преобразование
Лапласа,
– изображение.
№.
.
№.
=
.
№.
,
,
.
№.
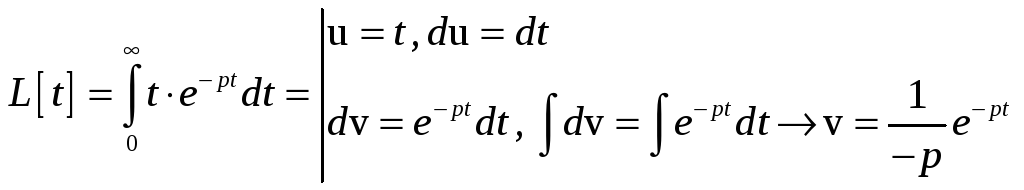. 5.
.
№.
.
№. Найдём преобразование Лапласа первой производной:
=
=
.
№. Найдём преобразование Лапласа второй производной:
=
=
=
.
№. Найти решение
уравнения
,
удовлетворяющее начальным условиям
Схема решения:
1. Подействуем преобразованием Лапласа на левую и правую части уравнения
.
2. Подействуем обратным преобразованием Лапласа на левую и правую части уравнения
(решение уравнения,
удовлетворяющее начальным условиям).
№.
,
1.
.