УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ФИЗИЧЕСКОЙ КУЛЬТУРЫ Кафедра теории физической культуры и биомеханики

Дятлов Д.А., Пушкарёв Е.Д., Шуркина Е.Н., Лобашова А.А.

Практикум по спортивной метрологии

(Краткий курс лекций и практических занятий)

издание 6-е, дополненное и переработанное

Челябинск 2012

1

«Шаблонное использование готовых рецептов, хотя бы даже опирающихся на самые тонкие математические соображения, ведёт не к умножению наших знаний, а к бесплатному расточению сил и нагромождению цифрового материала, мало

продвигающего вперёд наше понимание изучаемых явлений».

А.А.Чупров

(основоположник теории корреляций)

Учебно-методическое пособие предназначено для думающих студентов, пытающихся самостоятельно выполнить контрольные, курсовые и дипломные работы, а также для аспирантов и преподавателей, осмысленно занимающихся научно - исследовательской работой.

В пособии содержатся краткие теоретические сведения с практическими примерами решения расчётно-графических работ и вычислением основных статистических характеристик по курсу спортивной метрологии.

Выбор варианта работы соответствует порядковому номеру в списке группы текущего года (варианты работ приведена ниже).

2

3

1. Расчетно-графическая работа № 1.

Цель работы:

получить практические навыки анализа и обработки результатов измерений, определения значений границ доверительных интервалов, величины абсолютной и относительной погрешности результатов измерений.

1.1. Теоретические сведения.

Результат любого спортивного измерения (а также результат, показанный на соревнованиях или в контрольном упражнении - тесте) всегда имеет случайную погрешность. Другими словами, результат отдельного спортивного измерения есть случайная, изменяющаяся во времени величина. Это не означает, что определенный спортсмен в силу случайных колебаний измеряемых величин (спортивного результата) может показать любой результат, допустим, в соревновательном упражнении. Но и совершенно неверны такие рассуждения, что если спринтер А пробежал на соревновании 100 м за 10,2 с, а спринтер Б за 10,4 с, то спринтер А заведомо лучше подготовлен и должен всегда выигрывать у спринтера Б. Или, например, если спортсмен имеет лучший результат в прыжке в длину 8,20 м, то любой прыжок хуже 8 м не соответствует подготовленности данного человека (т.е. хуже, чем он может прыгать).

Приведенные выше рассуждения, на первый взгляд, могут показаться верными, или не верными, для организации тренировочного процесса. Действительно, на соревнованиях, как правило, места, очки, разряды, присваиваются за лучший результат. Но при управлении тренировочным процессом, когда тренеру необходимо ставить конкретные задачи на предстоящий период подготовки спортсмена, ориентировка на лучшие результаты уже недопустима. Как быть?

В этом случае необходимо из имеющихся у тренера результатов (ряда случайных чисел) выявить закономерности (например, истинные возможности спортсмена), которые и могут быть положены в основу управления тренировочным процессом.

Рассмотрим в виде примера распределение результатов спринтера, в течение

соревновательного периода, в беге на 100 м.

Таблица 1 Распределение результатов бега на 100 м по частотам в ранжированном ряду.

4

Как видно, истинные возможности данного спринтера позволяют ему пробегать 100 м за 10,5 с (так как эта величина встречается наибольшее количество раз). Остальные результаты (10,3; 10,4; 10,6; 10,7) являются случайными отклонениями от закономерных возможностей данного бегуна.

Разумеется, нельзя утверждать, что данный спортсмен не может показать результаты 10,2 и 10,8 с.

Следовательно, статистическая обработка результатов измерений, сводится к нахождению закономерности распределения, а именно, к нахождению наиболее вероятного результата и/или диапазона результатов, которые способен показать спортсмен, находясь на определенном уровне спортивной формы.

Рассмотрим порядок обработки результатов измерений, и вычисления случайной погрешности.

1.2.Порядок выполнения расчетно-графической работы № 1.

Упрыгуна в длину измерили ряд результатов выступления на соревнованиях (м).

7,22 7,53 7,44 7,35 7,19 7,45 7,60 7,32 7,66 7,47 Если график распределения результатов спортсмена соответствует кривой плотности

нормального распределения (закону нормального распределения), то мы можем вычислять среднюю арифметическую величину, среднее квадратическое отклонение, ошибку средней арифметической, доверительный интервал, величину случайной погрешности в абсолютной и относительной форме.

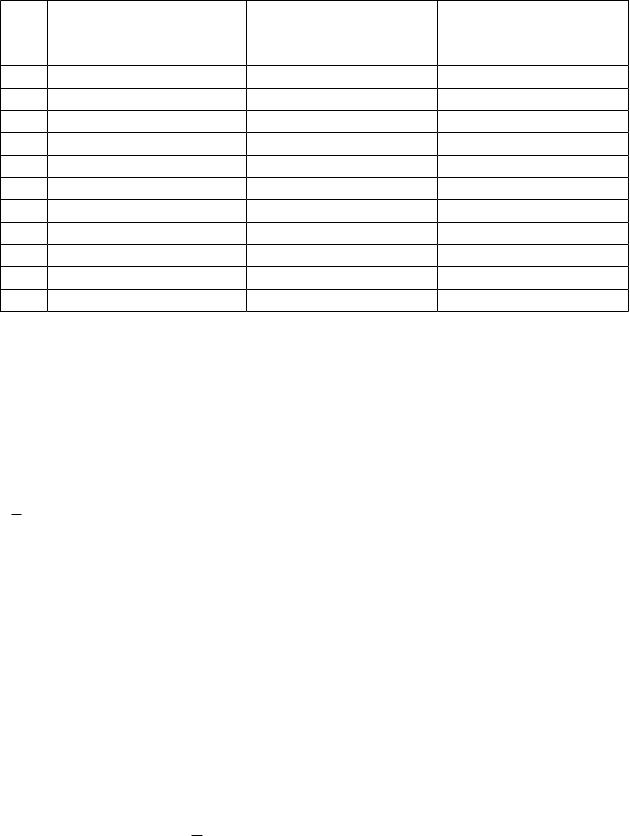
Для удобства обработки обычно оформляют таблицу (табл.2).

5

1. Вычислим значение средней арифметической величины по формуле (1):

где:

- средняя арифметическая величина.

е- знак суммирования,

i - результаты измерений.

n - объем выборки (кол-во измерений).

Выражение ехi читается как «сумма всех результатов измерения» (см. столбец 2, таблицы 2).

Средняя арифметическая величина обычно вычисляется на порядок точнее, чем измеряли. Для облегчения расчетов, желательно среднее арифметическое значение округлять (в нашем случае до сотых » 7,42 м).

Как относиться к полученной величине? По-видимому, мы можем утверждать, что впредь при таком же уровне спортивной формы наиболее часто будут встречаться результаты

6

равные или близкие »7,42 м., и именно этот результат будет отражать истинные возможности данного спортсмена.

Итак, мы нашли значение, обладающее наибольшей вероятностью своего появления, но не можем пока дать ответов на вопросы:

какие результаты вообще может показывать данный спортсмен?

может ли он в этом сезоне при таком уровне подготовленности (т.е. имея результат 7,42 м) выполнить, допустим, норматив мастера спорта (7,75 м)?

Для этого нам необходимо каким-то образом определить степень варьирования (изменения) результатов выступлений спортсмена на соревнованиях. Понятно, что если результаты у этого прыгуна будут изменяться очень сильно, то он будет показывать результаты в большом диапазоне, то есть, может показать, относительно среднего результата ( = 7,42), и очень хорошие для него результаты и очень плохие. Однако если вариативность результатов будет низкая, то его результаты будут близки к среднему значению.

Для определения степени варьирования результатов выполним ряд действий (шагов). 1 шаг. Определим отклонение каждого результата от средней арифметической

величины

( i - ) (3 столбец таблицы 2).

Например, для первого результата ( i - ) = 7,22 - 7,42 = -0,20 м, для второго - ( i -

) = 7,53 -7,42 = 0,11 м и т.д.

Витоге, мы находим степень варьирования каждого отдельного результата относительно средней арифметической, а нам необходимо оценить ряд измерений в целом. Для этого выполняем следующие действия.

2 шаг. Найдем квадраты отклонения каждого отдельного результата ( i - )2 (4 столбец таблицы 2).

Например, для первого результата -0,20 (3 столбец таблицы 2) возводим в квадрат -0,202 = 0,04, для второго ( i - )2 = 0,112 = 0,012 и т.д.

3 шаг. Найдем сумму квадратов отклонений е( i - )2.

В нашем случае она равна е( i - ) 2 = 0,2137 (4 столбец таблицы 2).

4 шаг. Вычислим среднее квадратическое отклонение по формуле (2):

7

где s - среднее квадратическое отклонение (сигма).

в среднем, на 0,154 м результаты в выборке отклоняются от средней арифметической

как в большую, так и в меньшую сторону. Чем больше сигма, тем больше степень варьирования результатов измерений относительно средней арифметической ( ).

Определение доверительного интервала.

Известно, что определить результат, на который способен спортсмен со 100% вероятностью невозможно. Однако диапазон (область) возможных результатов спортсмена определить можно. Действительно, если утверждать, что данный спортсмен может прыгнуть на 7,70 м, то почему нельзя предположить его прыжок на 7,71 м?

Диапазон (область) вероятных результатов спортсмена можно определить с помощью доверительного интервала. При прогнозе диапазона возможных результатов обычно используют следующие уровни вероятности: 95%; 99%; 99,9%.

Для того, чтобы определить значение доверительного интервала сначала необходимо вычислить ошибку средней арифметической.

Значение ошибки средней арифметической (m) - статистический показатель характеризующий степень точности измерения средней величины ( ).

Теперь рассчитаем границы доверительного интервала с вероятностью, например,

95%.

Например, Определим границы доверительного интервала для средней арифметической и ее стандартной ошибки ( ± m) с вероятностью 95%.

Математически эта связь выражается следующим образом:± Т(р,n) · m

8

где,

- средняя арифметическая;

m – ошибка средней арифметической;

Т - значение коэффициента, взятое из таблицы Т - критерия Стьюдента

(см. Приложение № 1 на стр.64). P – вероятность 95%.

n - число степеней свободы, которое вычисляют по формуле: (n = n - 1).

В приложении № 1 (см. стр. 64) по вертикали в таблице Т -критерия Стьюдента находим столбец № 1 (95%).

По горизонтали находим n - число степеней свободы. В нашем примере n = 10, то (n = n – 1 = 10 - 1 = 9). Пересечением этих двух координат (95% и 9) и будет являться значение коэффициента Т-критерия Стьюдента. В нашем примере это 2,26.

Полученное значение (Т=2,26) умножим на значение ошибки средней арифметической (m=0,05) из формулы 3 и получим границу доверительного интервала с

вероятностью 95%:

7,42 ± Т(р,n) · m = 7,42 ± 2,26 ґ 0,05 7,42 – (2,26 ґ 0,05) = 7,42 – 0,11 = 7,31 минимальная граница 7,42 + (2,26 ґ 0,05) = 7,42 + 0,11 = 7,53 максимальная граница Вывод по РГР№ 1.

С вероятностью равной 95% (то есть в 95 случаях из 100), при данном уровне подготовленности, спортсмен может показать на соревнованиях результат в интервале от 7,31 до 7,53 м.

Или в 95 случаях из 100 результаты этого прыгуна не будут выходить за пределы интервала от 7,31 до 7,53 м, а в 5 случаях его результат может выйти за максимальную или минимальную границу, т.е. спортсмен может показать на соревнованиях очень хороший или очень плохой результат.

Аналогично вычисляются значения доверительных интервалов с вероятностью 99%;

99,9%.

9