
- •Министерство образования и науки российской федерации
- •Введение
- •Лабораторная работа 1.
- •Анализ рынка недвижимости
- •(На примере рынка жилья Санкт-Петербурга)
- •Задание 1.
- •Задание 2.
- •Задание 3.
- •Пример результатов группировки средней цены 1 м2 жилья по площади квартир
- •Лабораторная работа 25. Оценка рыночной стоимости земельного участка под индивидуальное жилищное строительство с применением метода регрессионного анализа
- •Варианты заданий
- •Контроль качества и уточнение результатов оценки
- •Коэффициенты уравнения мр
- •Пример расчета стоимости земельного участка, используя полученное уравнение регрессии
- •Лабораторная работа 3. Временная оценка денежных потоков в практике оценки недвижимости
- •Методическая часть
- •2. Накопление денежной единицы за период
- •3. Фактор фонда возмещения (оf)
- •4. Текущая стоимость денежной единицы (реверсии)
- •5. Текущая стоимость аннуитета
- •6. Взнос на амортизацию денежной единицы
- •Лабораторная работа 4. Оценка рыночной стоимости объекта недвижимости методом сравнения рыночных продаж
- •Пример таблицы корректировок
- •Условия кредитных договоров для финансирования сделок с объектами-аналогами
- •Лабораторная работа 5. Оценка рыночной стоимости объекта недвижимости доходным подходом (методом ипотечно-инвестиционного анализа)
- •Библиографический список
- •Содержание
Варианты заданий
|
№ |
Столбцы |
Строки |
№ |
Столбцы |
Строки |
|
1 |
1,2,3,4,6,7,10 |
1-80 |
8 |
1,2,3,4,6,7,10 |
21-100 |
|
2 |
1,2,4,6,7,10,11 |
11-90 |
9 |
1,2,4,6,7,10,11 |
31-110 |
|
3 |
1,2,3,6,7,10,12 |
21-100 |
10 |
1,2,6,7,10,11,12 |
41-120 |
|
4 |
1,2,4,6,7,10,13 |
31-110 |
11 |
1,2,6,7,10,11,13 |
1-80 |
|
5 |
1,2,4,6,7,10,14 |
41-120 |
12 |
1,2,4,6,10,11,14 |
11-90 |
|
6 |
1,2,3,6,7,10,15 |
1-80 |
13 |
1,2,3,6,10,11,15 |
21-100 |
|
7 |
1,2,3,4,6,10,16 |
11-90 |
14 |
1,2,3,6,10,11,16 |
31-110 |
|
|
|
|
15 |
1,2,6,7,10,12,13 |
41-120 |
Все основные теоретические сведения по построению и использованию уравнения множественной регрессии приведены в [2]. Главные отличия данной работы – это построение нелинейной модели методом включения и построение интервального прогноза.
Множественная
регрессия – уравнение связи зависимой
переменной
![]() с
независимыми переменными
с
независимыми переменными![]() :
:
![]() (6)
(6)
В
зависимости от вида
![]() различают линейные и нелинейные
уравнения.
различают линейные и нелинейные
уравнения.
Линейное уравнение множественной регрессии имеет вид:
![]() (7)
(7)
где:
![]() -
параметры уравнения
-
параметры уравнения
Частным видом нелинейного уравнения множественной регрессии является уравнение вида:
![]() (8)
(8)
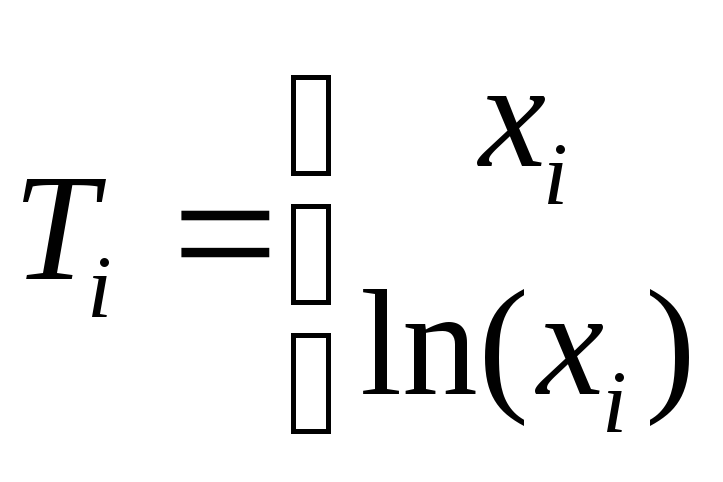 (9)
(9)
где:
![]() -
коэффициенты регрессии.
-
коэффициенты регрессии.
Таким
образом, в аддитивную модель входят или
сами факторы или их логарифмы. Использование
логарифма фактора
![]() ,
если фактор
,
если фактор![]() качественный,
не имеет смысла. В качестве
качественный,
не имеет смысла. В качестве![]() используем
единичный вектор, содержащийn
единиц, где n
- количество наблюдений, тогда смысл
используем
единичный вектор, содержащийn
единиц, где n
- количество наблюдений, тогда смысл
![]() -
свободный член в уравнении регрессии.
-
свободный член в уравнении регрессии.
Пусть исходные данные приведены в виде таблицы содержащей данные по 114 участкам. Фрагмент таблицы приведен на рис. 1.
Уравнения множественной регрессии могут включать в качестве независимых переменных фиктивные переменные, которые используются для обозначения качественные признаков (наличие электричества, воды, канализации, и др.). Чтобы ввести такие переменные в регрессионную модель присвоим им значения «1» - если данный фактор присутствует, «0» - в противоположном случае.

Рис.1. Исходные данные
Для выявления связей между факторами и откликом проведем предварительный анализ, используя инструмент «Анализ данных» Корреляция. Результат приведен на рис.2.
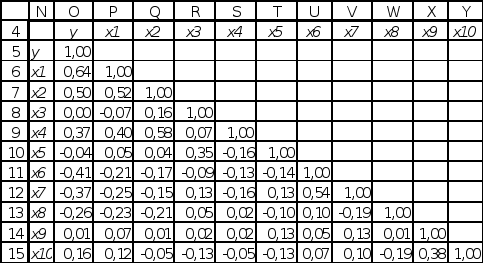
Рис.2. Исходные данные
Анализ коэффициентов парной корреляции показывает, что отклик (цена) заметно коррелирует с факторами «наличие электричества», «наличие воды» и «расстояние до административного центра» (коэффициенты парной корреляции по модулю выше 0.4). Судя по вычисленному коэффициенту корреляции между ценой и фактором «наличие газа» (он практически равен нулю), связь между ними отсутствует. Фактор «наличие средств связи» заметно коррелирован с факторами «наличие электричества» и «наличие воды», что служит доводом в пользу наличия мультиколлинеарности между факторами.
Для построения модели будем использовать пошаговый метод включения, который позволяет избежать включения в уравнение малоинформативных факторов и мультиколлинеарности между ними.
Суть метода включения — в последовательном включении переменных в модель до тех пор, пока качество регрессионной модели будет повышаться. Первыми включаются в регрессионное уравнение факторы, имеющие относительно исследуемого показателя большее значение коэффициента корреляции.
Схема применения этого метода включения для линейной модели подробно описана в [2]. В отличие от чисто линейной модели на каждом шаге необходимо пытаться включить в уравнение не только сам фактор, но и его логарифм (для факторов, не являющихся качественными переменными).
Пусть
k
– номер шага. На k-м
шаге (k=1)
с помощью табличной функции ЛИНЕЙН( )
найдем наиболее информативную переменную
среди
![]() и
и
![]() .
Методом перебора устанавливаем, что
это
.
Методом перебора устанавливаем, что
это
![]() (рис. 3).
(рис. 3).
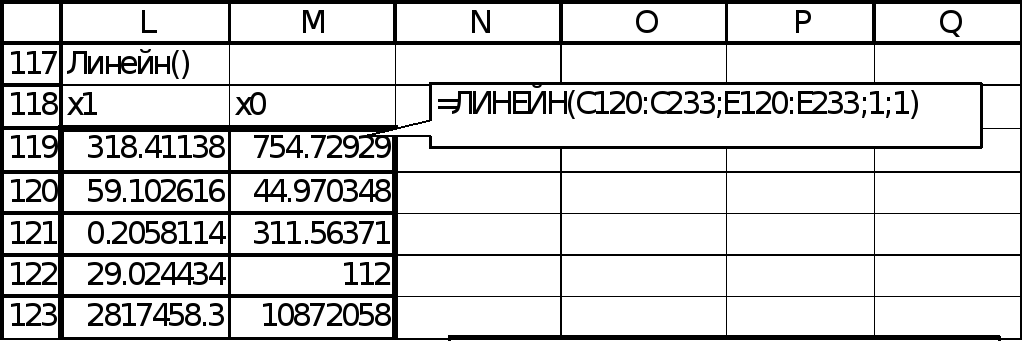
Рис. 3.
2-й
шаг (k=2). Среди всевозможных пар (![]() ,
,![]() ),
и (
),
и (![]() ,
,![]() )
выбирается наиболее информативная
пара, путем последовательного применения
табличной функции ЛИНЕЙН к различным
парам.
)
выбирается наиболее информативная
пара, путем последовательного применения
табличной функции ЛИНЕЙН к различным
парам.
Анализируя
R2,
приходим к выводу, что наиболее
информативной парой является пара
(![]() ,
,![]() )
(рис. 4).
)
(рис. 4).
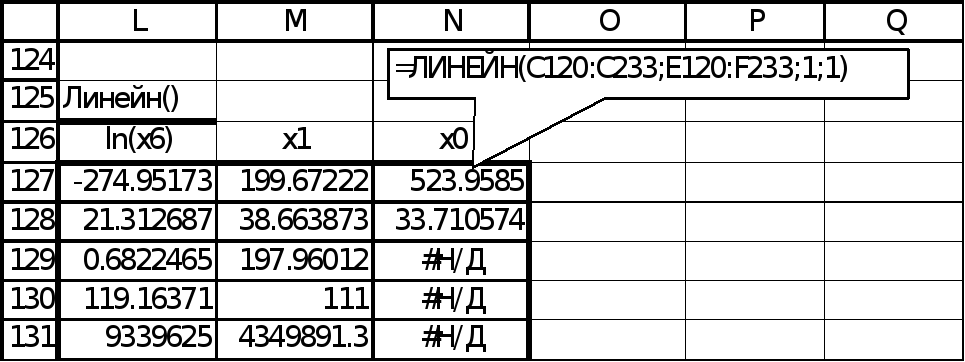
Рис. 4
С
включением
![]() коэффициент
детерминации существенно вырос,
следовательно, это правильное решение.
коэффициент
детерминации существенно вырос,
следовательно, это правильное решение.
3-й
шаг (k=3).
Среди всевозможных троек (![]() ,
,![]() ,
,![]() ),
и (
),
и (![]() ,
,![]() ,
,![]() ),
выбирается наиболее информативная (в
смыслеR2)
тройка. Последовательно применяя
табличную функцию ЛИНЕЙН к различным
тройкам, приходим к выводу, что наиболее
информативной тройкой является (
),
выбирается наиболее информативная (в
смыслеR2)
тройка. Последовательно применяя
табличную функцию ЛИНЕЙН к различным
тройкам, приходим к выводу, что наиболее
информативной тройкой является (![]() ,
,![]() ,
,![]() ) (рис.5).
) (рис.5).
С включением x2 коэффициент детерминации существенно вырос, следовательно, его включение оправдано без анализа R2adj.
4-й
шаг (k=4). Среди всевозможных четвёрок
(![]() ,
,![]() ,
,![]() ,
,![]() )
и (
)
и (![]() ,
,![]() ,
,![]() ,
,![]() ),
ищется наиболее информативная, путем
последовательного применения табличной
функции ЛИНЕЙН к различным четвёркам.
),
ищется наиболее информативная, путем
последовательного применения табличной
функции ЛИНЕЙН к различным четвёркам.
Наиболее
информативной четвёркой является
(![]() ,
,![]() ,
,![]() ,
,![]() )(рис. 6-7).
)(рис. 6-7).

Рис. 5
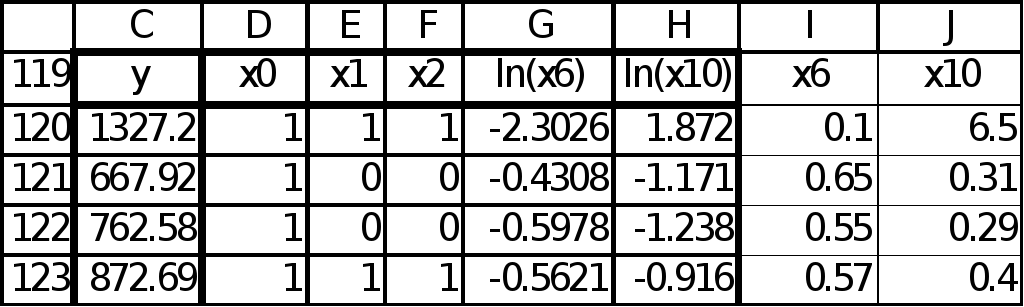
Рис. 6
С включением ln(x10) коэффициент детерминации R2 существенно вырос, с 0,717 до 0,73, следовательно, его включение оправдано без анализа R2adj.
5-й шаг (k=5). При добавлении пятой переменной в уравнение регрессии среди всевозможных комбинаций (х1, ln(x6), х2, ln(x10), xj) и (х1, ln(x6), х2, ln(x10), ln(xj)), не удалось найти такую, которая существенно улучшает модель.
Поэтому, более подробно исследуем уравнение, полученное после 4-х шагов.
![]() , (10)
, (10)
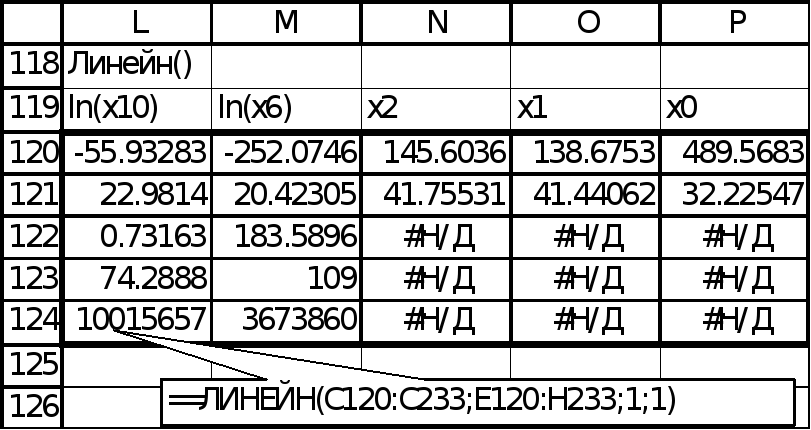 .Рис.
7
.Рис.
7
![]() (11)
(11)
Для исследования этой модели, применив инструмент “Регрессия” надстройки «Пакет Анализа» MS Excel (рис. 8). Коэффициент детерминации R2 равен 0,732. Это значение показывает, что 73,2% вариации цены объясняется этим уравнением. Высокое качество уравнения, также подтверждается значимостью уравнения в целом (значимость F существенно ниже уровня значимости в 5%). На рис. 8-9 представлен фрагмент отчёта регрессии по четырем указанным факторам.
В уравнении (11) все коэффициенты значимы, на уровне значимости 5%. Необходимо заметить, что коэффициент при x10 наименее значим (р-значение равно 1,7%).
Проверка качества уравнения
Для проверки адекватности уравнения необходимо проверить выполнение условий Гаусса-Маркова.
Проверим однородность (гомоскедастичность) остатков с помощью метода Гольдфельда-Квандта (Goldfeld-Quandt).
Основная идея теста Гольдфельда-Квандта состоит в следующем:
упорядочение n наблюдений по возрастанию фактора;
исключение из рассмотрения C центральных наблюдений; при этом
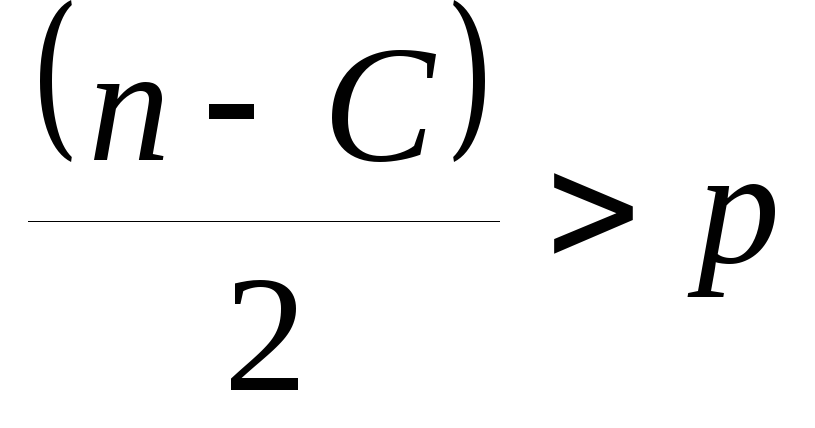 ,
где
,
где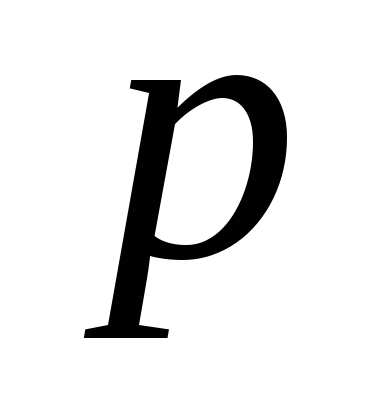 – число оцениваемых параметров, для
нашей модели
– число оцениваемых параметров, для
нашей модели равно 4;
равно 4;разделение совокупности из (n-C) наблюдений на две группы (соответственно с малыми и большими значениями Х) и определение по каждой группе уравнений регрессии;
определение остаточной суммы квадратов для первой (S1) и второй (S2) групп и их отношения F=S1/S2 , если S1>S2 или
F= S2/ S1 , если S1<S2.
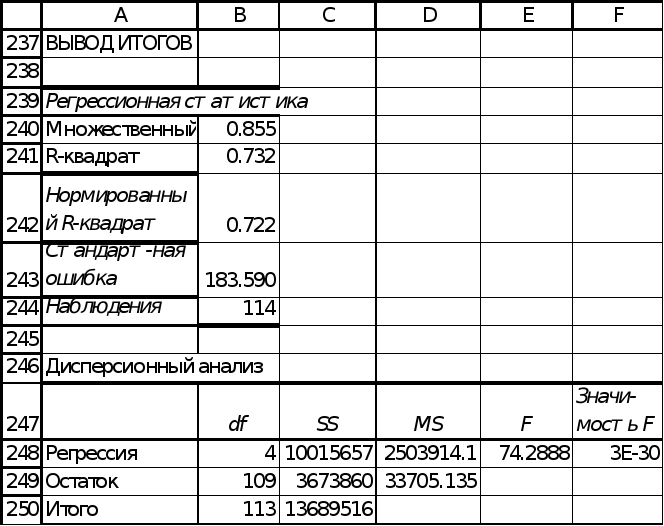
Рис. 8. Фрагмент отчёта MS Excel “Регрессия”. Начало
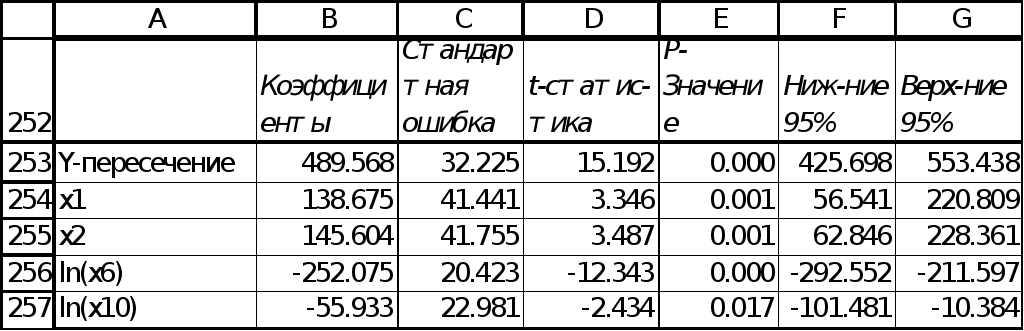
Рис. 9. Фрагмент отчёта MS Excel “Регрессия”. Окончание
При
выполнении нулевой гипотезы о
гомоскедастичности отношение F
будет удовлетворять F-критерию
со степенями свободы
![]() для каждой остаточной суммы квадратов.
для каждой остаточной суммы квадратов.
Эту
операцию необходимо проверить по каждому
из факторов. Выполним это для фактора
![]() .
Для этого скопируем на другой лист
данные, содержащие факторы, входящие в
уравнение и столбец, содержащий остатки,
вместе с заголовками столбцов. После
этого, упорядочиваем данные по величине
.
Для этого скопируем на другой лист
данные, содержащие факторы, входящие в
уравнение и столбец, содержащий остатки,
вместе с заголовками столбцов. После
этого, упорядочиваем данные по величине![]() .
В качестве величины С возьмем 35
(приблизительно 30% от общего числа
наблюдений), т.е. исключим 35 центральных
наблюдений (рис.10).
Далее первые
.
В качестве величины С возьмем 35
(приблизительно 30% от общего числа
наблюдений), т.е. исключим 35 центральных
наблюдений (рис.10).
Далее первые
![]() =
40 остатков считаем первой выборкой
(диапазон F2:F41), последние
=
40 остатков считаем первой выборкой
(диапазон F2:F41), последние![]() =
40 остатков (диапазон F76:F115), считаем
второй выборкой.
=
40 остатков (диапазон F76:F115), считаем
второй выборкой.
Для
проверки однородности остатков
воспользуемся критерием Фишера для
проверки равенства дисперсий рис. 11
. Результаты
приведены на рис.
12. Поскольку
наблюдаемое F
(1,32) меньше F
критического (1,70), то гипотеза о равенстве
дисперсий
подтверждается, таким образом, однородность остатков (гомоске-дастичности)
по фактору
![]() наблюдается.
наблюдается.
Аналогичную проверку необходимо провести для каждого из факторов!
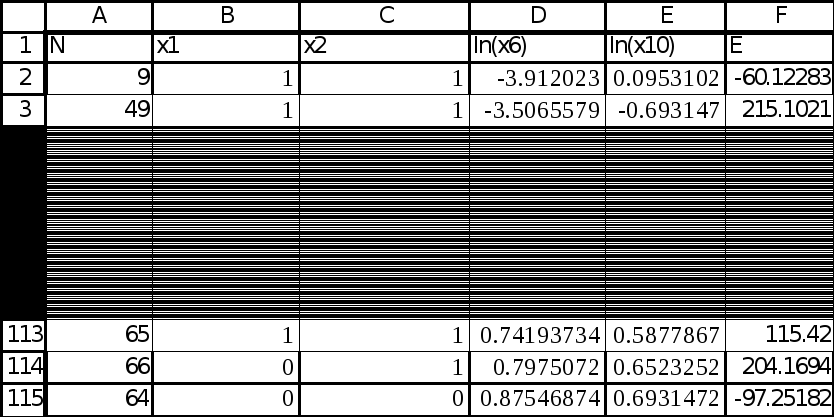
Рис.
10.
Фрагмент отчёта MS
Excel
. Проверка гомоскедастичности
остатков по фактору
![]() .
Упорядоченный массив данных по
.
Упорядоченный массив данных по![]()
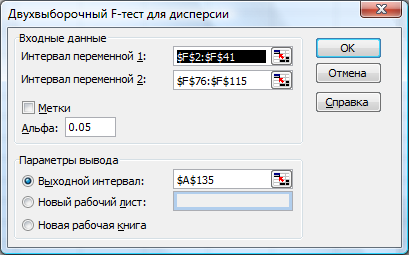
Рис.
11. Фрагмент отчёта MS
Excel.
Проверка гомоскедастичности
остатков по фактору
![]() .
Диалоговое окно критерияF-теста
.
Диалоговое окно критерияF-теста
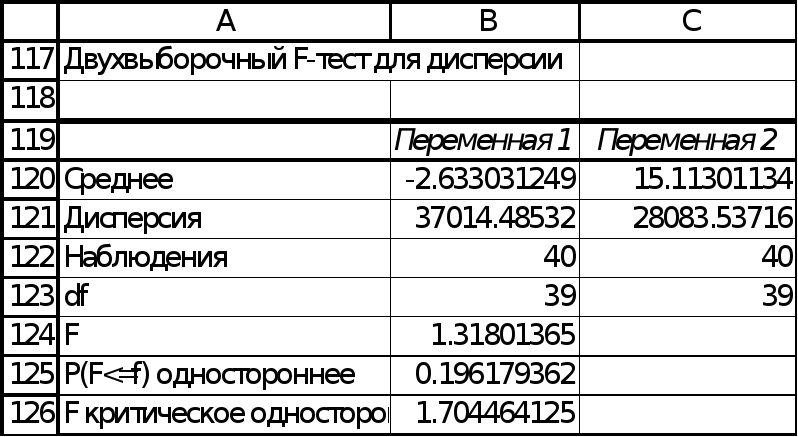
Рис.
12.
Фрагмент отчёта MS
Excel.
Проверка гомоскедастичности
остатков по фактору
![]() .
Применение критерия Фишера.
.
Применение критерия Фишера.
