
- •Производная функции, ее геометрический смысл.
- •Производная суммы, произведения и частного.
- •3.Производная сложной функции. Производная обратной функции
- •Дифференциал функции
- •Геометрический смысл дифференциала
- •Связь дифференциала с производной
- •2. Дифференциал суммы, произведения и частного.
- •4. Функции, заданные параметрически, их дифференцирование.
- •1. Производные высших порядков Понятие производных высших порядков
- •Формула Лейбница
- •4. Правило Лопиталя раскрытия неопределенностей
4. Правило Лопиталя раскрытия неопределенностей
Теорема.
Пусть
функции
![]() и
и![]() определены и дифференцируемы в некоторой
окрестности точки
определены и дифференцируемы в некоторой
окрестности точки![]() ,
за исключением, быть может, самой точки
,
за исключением, быть может, самой точки![]() .
Пусть также
.
Пусть также![]() и
и![]() в указанной окрестности точки
в указанной окрестности точки![]() .
Тогда, если существует предел отношения
производных
.
Тогда, если существует предел отношения
производных![]() (конечный или бесконечный), то существует
и предел
(конечный или бесконечный), то существует
и предел![]() ,
причем справедлива формула
,
причем справедлива формула
![]() . (3)
. (3)
Замечание
1. Теорема
остается справедливой и в случае, когда
![]() ,
,![]() .
.
Замечание
2. Если
производные
![]() и
и![]() удовлетворяют
тем же требованиям, что и сами функции
удовлетворяют
тем же требованиям, что и сами функции![]() и
и![]() ,
то правило Лопиталя можно применить
повторно. При повторном применении
правила Лопиталя рекомендуется сначала
провести все возможные упрощения,
например, сократить общие множители и
использовать уже знакомые пределы.
,
то правило Лопиталя можно применить
повторно. При повторном применении
правила Лопиталя рекомендуется сначала
провести все возможные упрощения,
например, сократить общие множители и
использовать уже знакомые пределы.
Замечание
3.
Правило Лопиталя называют ещё правилом
раскрытия неопределенностей, так как
с его помощью находятся пределы
неопределенных выражений. Так,
неопределенностью вида
![]() называется отношение двух функций
называется отношение двух функций![]()
![]() при
при![]() ,
если
,
если
![]() .
.
Раскрыть
неопределенность – это значит вычислить
![]() ,
если он существует, или установить, что
он не существует.
,
если он существует, или установить, что
он не существует.
Примеры.
1.
![]() =
= .
.
2.![]() .
.
3.
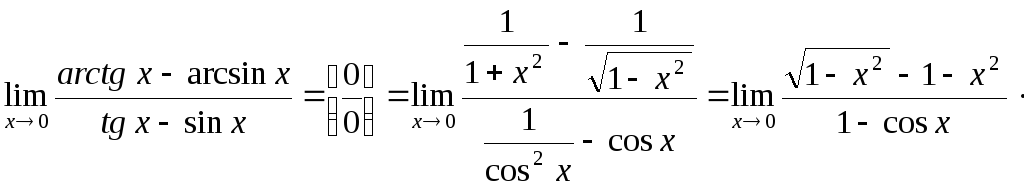
![]()
![]()
 .
.
Если
при
![]() (
(![]() )
обе функции
)
обе функции![]() и
и![]() одновременно стремятся к бесконечности,
то есть
одновременно стремятся к бесконечности,
то есть
![]() ,
,
то
отношение двух функций
![]()
![]() при
при![]() представляет собой неопределенность
типа
представляет собой неопределенность
типа![]() .
Можно доказать, что правило Лопиталя
справедливо и в этом случае.
.
Можно доказать, что правило Лопиталя
справедливо и в этом случае.
Примеры.
1. .
.
2.![]() .
.
3.![]() .
.
Из последних двух примеров можно сделать вывод о том, что многочлен любой степени растет медленнее показательной функции.
Кроме рассмотренных случаев встречаются ещё неопределенности следующих видов.
Неопределенность
вида
![]() .
Это обозначение указывает, что при
заданном изменении независимой переменной
х (
.
Это обозначение указывает, что при
заданном изменении независимой переменной
х (
![]() или
или![]() )
функция, предел которой требуется найти
, представляется разностью двух функций,
стремящихся к положительной бесконечности.
)
функция, предел которой требуется найти
, представляется разностью двух функций,
стремящихся к положительной бесконечности.
Этот
случай сводится к неопределенностям
типа
![]() или
или![]() преобразованиями.
преобразованиями.
Пример.

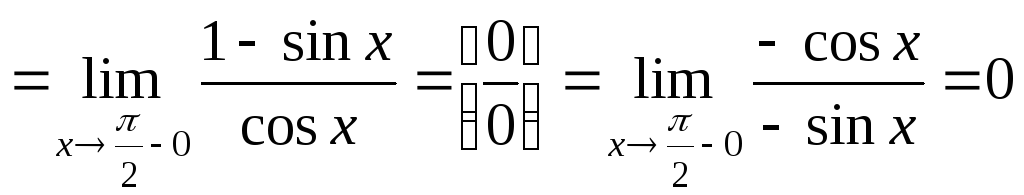 .
.
Неопределенность
вида
![]() .
Это обозначение указывает, что при
заданном изменении независимой переменной
х (
.
Это обозначение указывает, что при
заданном изменении независимой переменной
х (
![]() или
или![]() )
функция, предел которой требуется найти
, представляется произведением функции,
стремящейся к нулю и функции, стремящейся
к бесконечности.
)
функция, предел которой требуется найти
, представляется произведением функции,
стремящейся к нулю и функции, стремящейся
к бесконечности.
Пример.

 .
.
Неопределенность
вида
![]() .
Это обозначение указывает, что при
заданном изменении независимой переменной
х (
.
Это обозначение указывает, что при
заданном изменении независимой переменной
х (
![]() или
или![]() )
функция, предел которой требуется найти
, представляется степенью, основание
которой стремится к единице, а показатель
– к бесконечности.
)
функция, предел которой требуется найти
, представляется степенью, основание
которой стремится к единице, а показатель
– к бесконечности.
Неопределенность
вида
![]() .
Это обозначение указывает, что при
заданном изменении независимой переменной
х (
.
Это обозначение указывает, что при
заданном изменении независимой переменной
х (
![]() или
или![]() )
функция, предел которой требуется найти
, представляется степенью, основание
которой стремится к бесконечности, а
показатель – к нулю.
)
функция, предел которой требуется найти
, представляется степенью, основание
которой стремится к бесконечности, а
показатель – к нулю.
Неопределенность
вида
![]() .
Это обозначение указывает, что при
заданном изменении независимой переменной
х (
.
Это обозначение указывает, что при
заданном изменении независимой переменной
х (
![]() или
или![]() )
функция, предел которой требуется найти
, представляется степенью и основание
и показатель которой стремятся к нулю.
)
функция, предел которой требуется найти
, представляется степенью и основание
и показатель которой стремятся к нулю.
Неопределенности
типов
![]() ,
,
![]() ,
,
![]() приводятся к неопределенностям типов
приводятся к неопределенностям типов
![]() или
или![]() с
помощью логарифмирования. Функция
предварительно логарифмируется, и
сначала отыскивается предел не заданной
функции, а её логарифма, а затем уже по
пределу логарифма находится предел
функции, что допустимо вследствие
непрерывности логарифма.
с
помощью логарифмирования. Функция
предварительно логарифмируется, и
сначала отыскивается предел не заданной
функции, а её логарифма, а затем уже по
пределу логарифма находится предел
функции, что допустимо вследствие
непрерывности логарифма.
Примеры.
1.![]() .
Рассмотрим предел
.
Рассмотрим предел
![]() .
.
Так
как
![]() ,
то
,
то![]() .
.
