
- •Раздел первый
- •1.2. Аксиомы статики
- •1.3. Аналитическое задание и сложение сил
- •1.4. Связи и реакции связей
- •Глава2. Системы сходящихся и параллельных сил
- •2.1. Сложение и равновесие системы сходящихся сил
- •2.2. Сложение системы параллельных сил
- •2.3. Пара сил
- •2.4. Момент силы относительно точки
- •Глава 3. Плоская система сил
- •3.1. Условия равновесия плоской системы сил
- •3.2. Приведение плоской системы сил к данному центру
- •3.3. Приведение произвольной плоской системы сил к равнодействующей
- •3.4. Равновесие системы тел
- •3.5. Равновесие тел при наличии трения
- •3.5.1. Трение скольжения
- •3.5.2. Трение качения
- •Глава 4. Пространственная система сил
- •4.1. Момент силы как вектор
- •4.2. Момент силы относительно оси
- •4.3. Приведение пространственной системы сил к данному центру
- •4.4. Условия равновесия произвольной системы сил
- •4.5. Центр параллельных сил
- •4.6.Центр тяжести однородных тел
4.3. Приведение пространственной системы сил к данному центру
По аналогии с плоской системой любую пространственную систему можно упростить, если на основе теоремы о параллельном переносе силы перенести все заданные силы в произвольную точку 0.
П усть
дана пространственная система сил
усть
дана пространственная система сил
![]() .
.
Для ее упрощения перенесем все силы в произвольную точку 0 (рис. 1.43).
После параллельного переноса всех сил в точку 0 получим систему сходящихся сил, которую по аксиоме 3 можно заменить одной силой, называемой главным вектором системы:
|
|
(1.27) |
Складывая геометрически векторы присоединенных пар сил, получим одну пару сил, момент которой называется главным моментом системы:
|
|
(1.28) |
Таким образом, любую пространственную систему сил можно заменить одним главным вектором и одним главным моментом (рис. 1.44).
В еличина
и направление главного вектора и главного
момента определяются из следующих
уравнений:
еличина
и направление главного вектора и главного
момента определяются из следующих
уравнений:
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
Случаи приведения пространственной системы сил
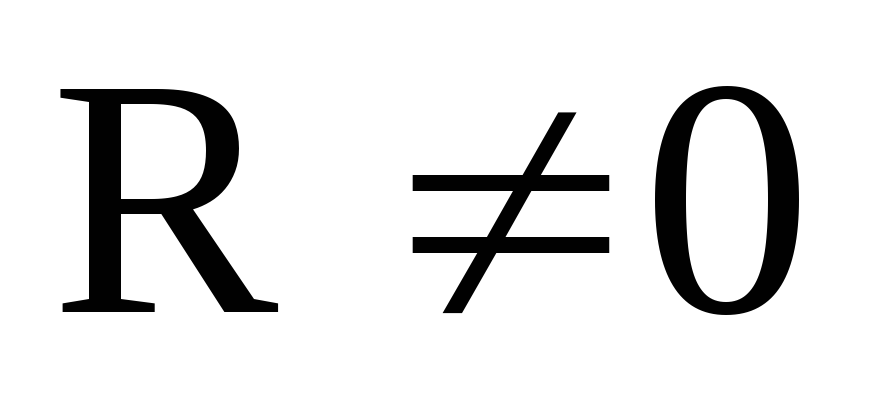 ;
;
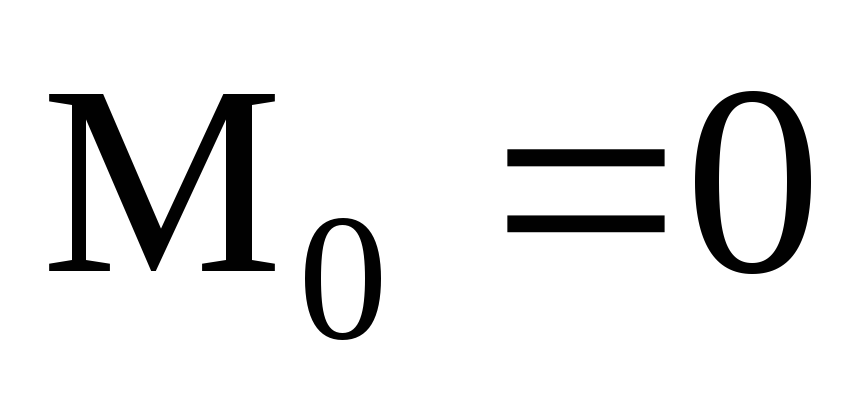 – в этом единственном случае система
сил привелась к одной равнодействующей,
т.е. главный вектор системы является
его равнодействующей.
– в этом единственном случае система
сил привелась к одной равнодействующей,
т.е. главный вектор системы является
его равнодействующей.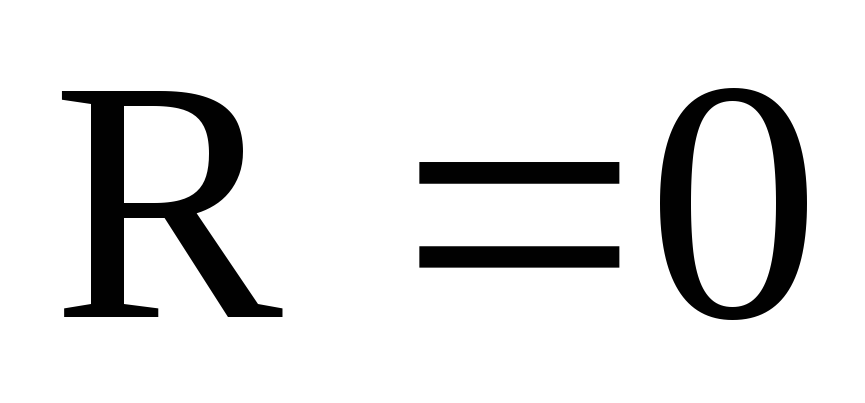 ;
;
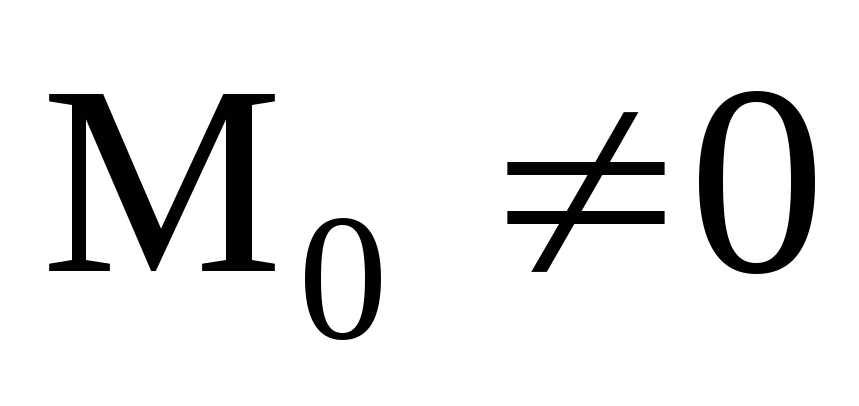 – в этом случае система сил привелась
к одной паре сил. Очевидно величина и
направление главного момента в этом
случае не зависят от выбора центра
приведения.
– в этом случае система сил привелась
к одной паре сил. Очевидно величина и
направление главного момента в этом
случае не зависят от выбора центра
приведения.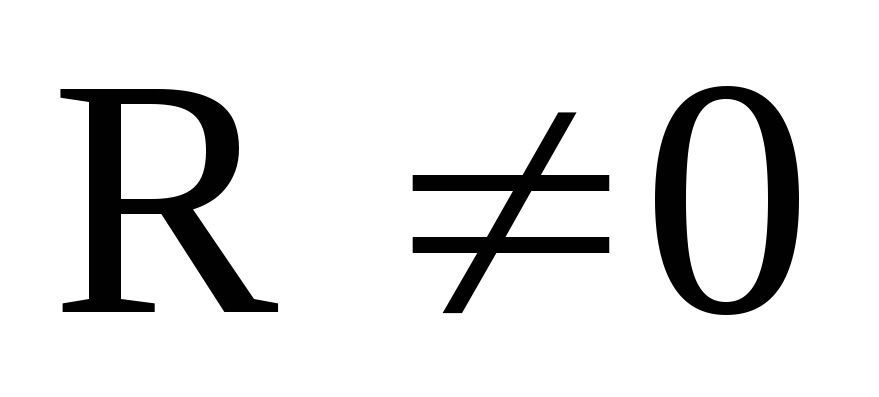 ;
;
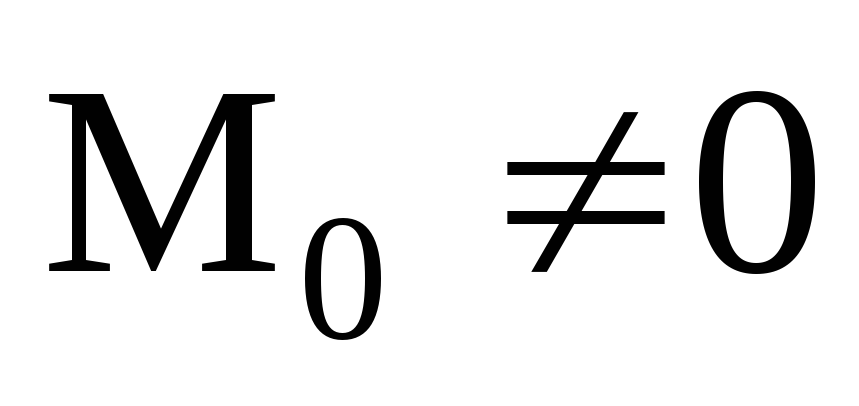 ;
;
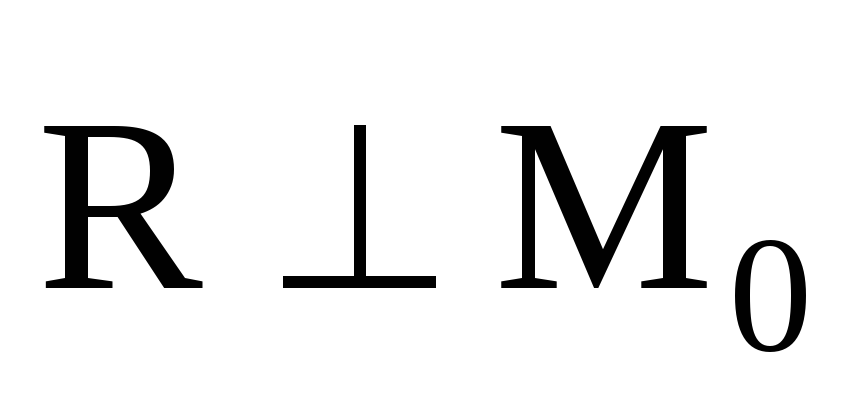 – в данном случае имеем плоскую систему
сил, которую как было показано выше,
всегда можно заменить равнодействующей
в новом центре приведения.
– в данном случае имеем плоскую систему
сил, которую как было показано выше,
всегда можно заменить равнодействующей
в новом центре приведения.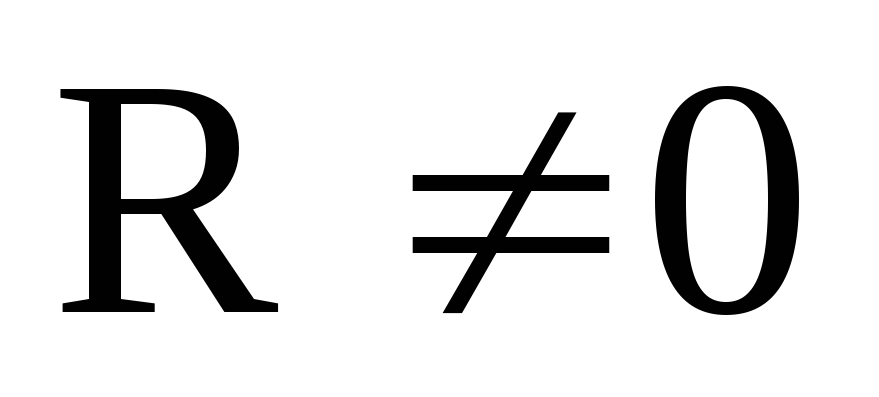 ;
;
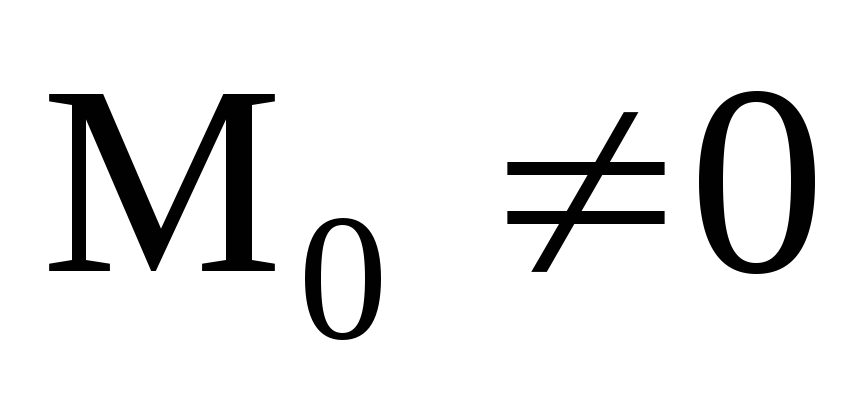 ;
;
 – динама (динамический винт). В этом
случае тело совершает сложное (винтовое)
движение.
– динама (динамический винт). В этом
случае тело совершает сложное (винтовое)
движение. ;
;
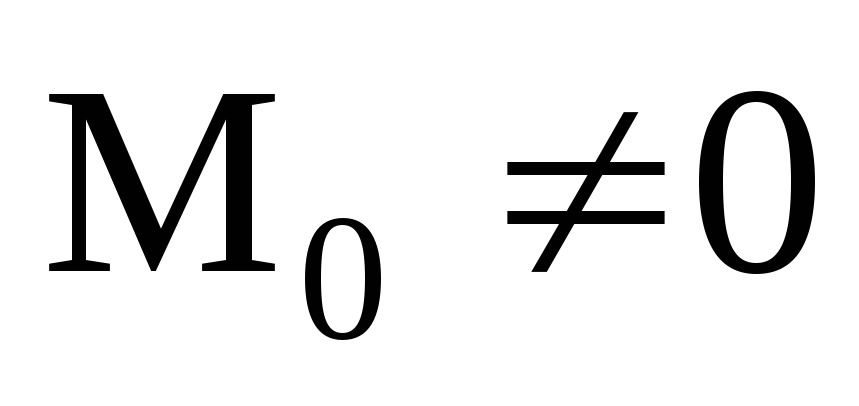 ;
;
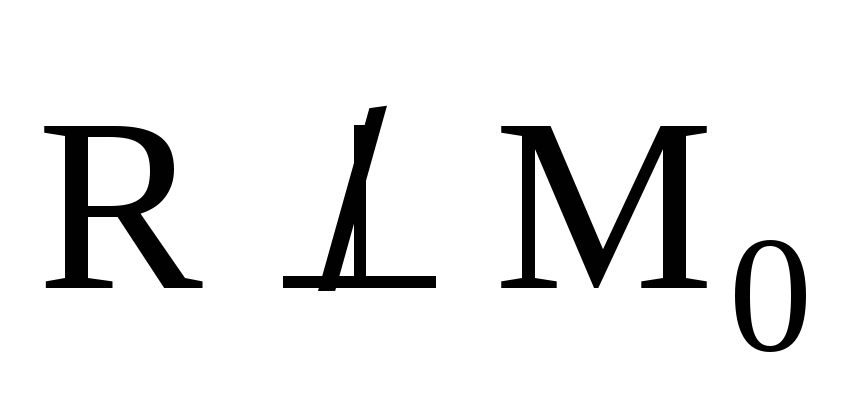 ;
;
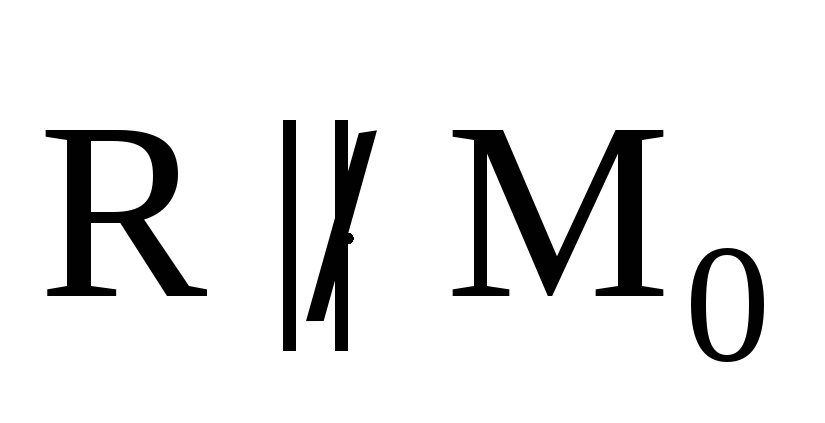 – общий случай, который всегда можно
привести к динаме в новом центре
приведения.
– общий случай, который всегда можно
привести к динаме в новом центре
приведения. ;
;
 – случай равновесия пространственной
системы сил.
– случай равновесия пространственной
системы сил.
4.4. Условия равновесия произвольной системы сил
Для равновесия пространственной системы сил в общем случае необходимо и достаточно, чтобы главный вектор и главный момент системы в одно и тоже время равнялись бы нулю, т.е.
|
|
(1.29) |
Проектируя (1.27) и (1.28) на оси координат, получим:
|
|
(1.30) |
|
|
(1.31) |
Инварианты (приведения) пространственной системы сил
Инвариантами будем называть параметры, которые не изменяются при перемене центра приведения.
Очевидно первым инвариантом системы является главный вектор системы, так как его величина и направление не зависят от центра приведения.
Можно показать, что вторым инвариантом системы является скалярное произведение главного вектора на вектор главного момента:
![]()
Пример 1.8. Определить реакции связей для однородной плитыABDE(в точке А – сферический шарнир, в точкеB- цилиндрический шарнир, в точке С – гибкая нить) (рис. 1.45).
Решение.Составим уравнения равновесия плиты на основе условий равновесия (1.30), (1.31).

|
|
(а) |
|
|
(б) |
|
|
(в) |
|
|
(г) |
|
|
(д) |
|
|
(е) |
Решая полученную
систему уравнений, находим: из (6) –
![]() ;
из (д) –
;
из (д) –![]() ;
из (г) –
;
из (г) –![]() ;
из (в) –
;
из (в) –![]() ;
из (б) –
;
из (б) –![]() ;
из (а) –
;
из (а) –![]() .
.
Отрицательное
значение
![]() указывает на то, что в действительности
это реакция направлена в противоположную
сторону. Углыиопределяются размерами плиты.
указывает на то, что в действительности
это реакция направлена в противоположную
сторону. Углыиопределяются размерами плиты.
