L№1опред

Текст лекции.

1. Определители второго и третьего порядка, их свойства.

Пусть - вещественные числа. Число

(1)

называется определителем второго порядка, а числа - его элементами.

Определитель (1) удобно записывать следующим образом:

В скобках схематически изображено правило, по которому вычисляется оп­ределитель второго порядка.

Пример.

Пусть - вещественные числа. Составим из этих чисел три определителя второго порядка:

Число

(2)

называется определителем третьего порядка, а числа - его элементами.

Договоримся называть диагональ, образованную элементами , главной, а диагональ, образованную элементами , - побочной.

Формула (1) для определителя (2) дает:

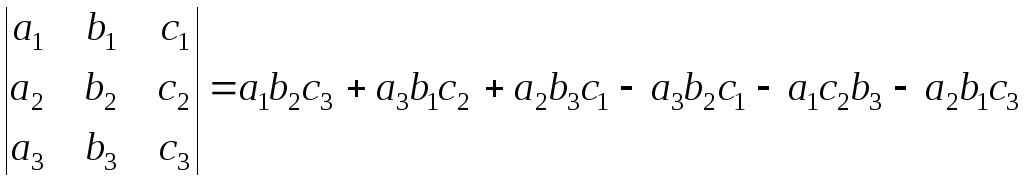(3)

Формула (3) называется правилом Сарруса и схематически выглядит следующим образом:

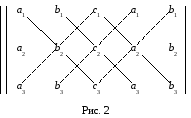
Укажем другое правило составления выражений для определителя, еще менее требующее напряжения внимания и памяти. Для этого к таблице, из которой составлен определитель, допишем справа еще раз первый, а затем второй столбец.

Сплошной чертой соединены тройки членов, получаемые параллельным переносом главной диагонали и отвечающие трем слагаемым, входящим в выражение (3) со знаком плюс; пунктиром соединены три другие тройки членов, получаемые параллельным переносом побочной диагонали и отвечающие трем слагаемым, входящим в выражение (3) со знаком минус.

Пример. Вычислить определитель третьего порядка, пользуясь:

а) определением (2);

б) правилом Саррюса (3).

Решение:

а)

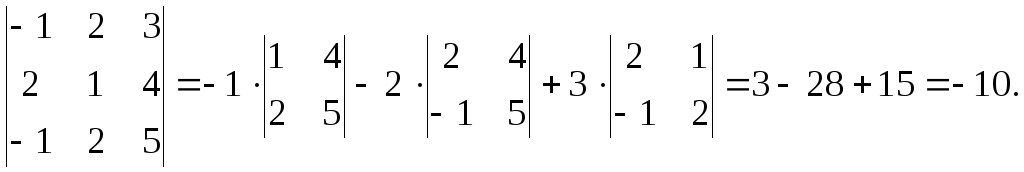
б) .

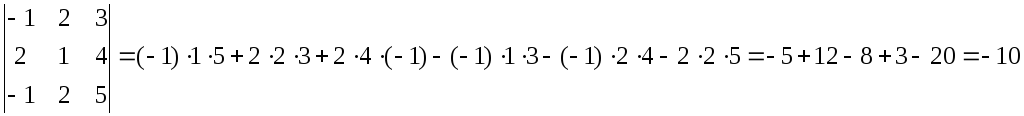2. Алгебраические дополнения и миноры.

По аналогии с определителем третьего порядка можно определить определители четвертого, пятого и так далее порядков. Понятие определи­теля n-го порядка введем индуктивно, считая, что нами уже введено поня­тие определителя n-1-го порядка.

Пусть дано вещественных чисел, для изображения которых исполь­зуем одну букву с двумя индексами:

(4)

Расположим эти числа в строк, и полученную таблицу заключим в верти­кальные черточки:

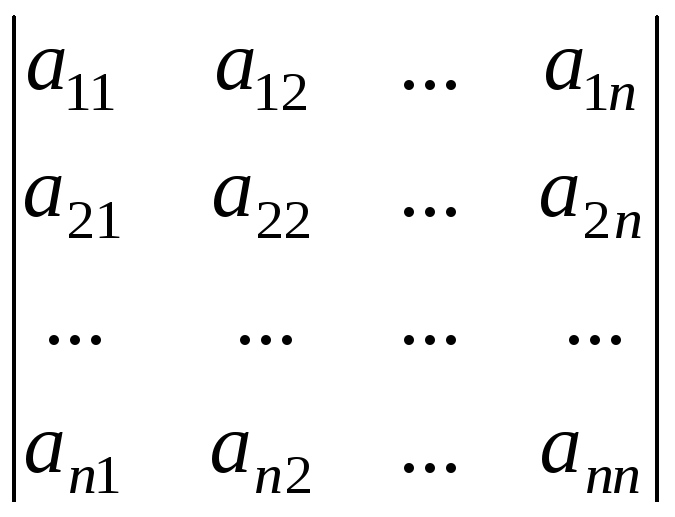(5)

Таким образом обозначается определитель n-го порядка; при этом числа (4) называются элементами определителя n-го порядка.

Определитель (5) обозначают также кратко: , или , где первый индекс указывает на номер строки, а второй индекс - на номер столбца, которым принадлежит элемент , .

Итак,

.

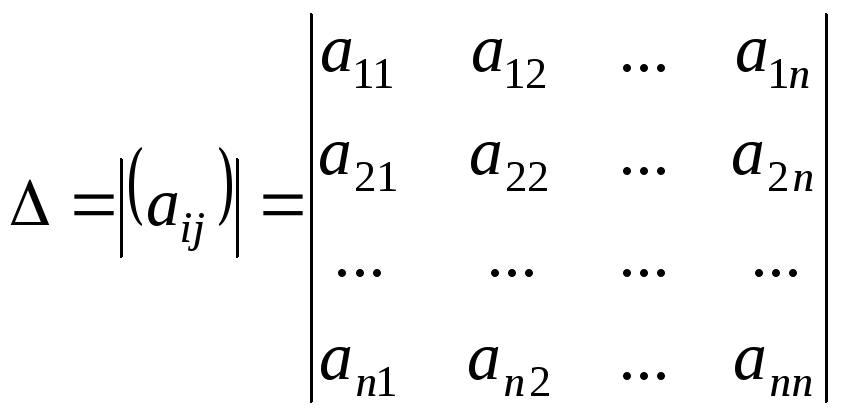Определение. Минором любого элемента определи­теля (5) называется определитель n-1-го порядка, который получа­ется из определителя (5) в результате вычеркивания i-ой строки и j-го столбца.

Например, для определителя второго порядка

Определитель третьего порядка

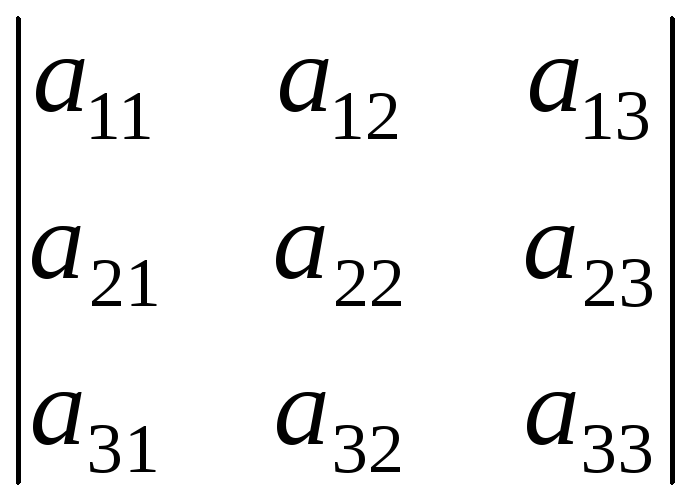
имеет 9 миноров, которые являются определителями второго порядка. В частности, определители

-

являются минорами элементов .

Определение. Число называется алгебраическим дополнением элемента определителя (5).

Пример. Вычислить определитель четвертого порядка:

.

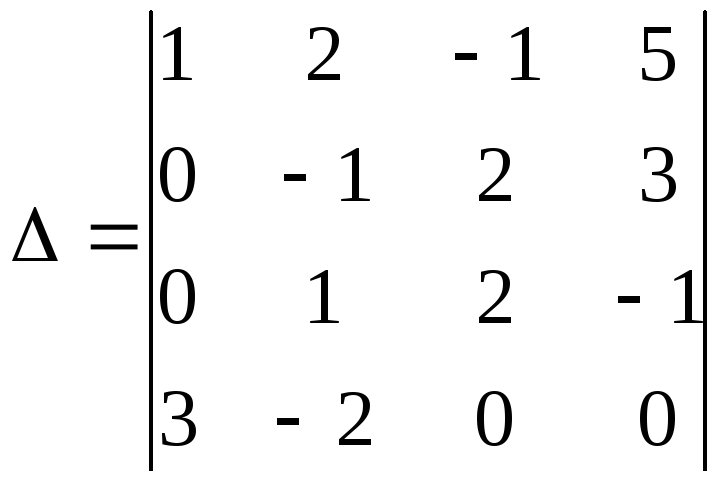Решение. Найдем миноры элементов первой строки:

Откуда

По определению определителя имеем: