Вопросы для контроля знаний

1. При каком внутреннем силовом факторе возникает кручение?

2. Какие напряжения возникают в поперечных сечениях при кручении?

3. Как рассчитать максимальные напряжения при кручении?

4. Что такое полярный момент сопротивления и полярный момент инерции?

5.Напишите условие прочности при кручении.

6. Какая деформация возникает при кручении?

7. Как рассчитать угол закручивания круглого вала?

8. Как определяется допускаемое касательное напряжение ?

9. Как рассчитать необходимый диаметр вала при кручении, если и характер нагружения вала известны?

Пример № 17 (каримов)

Прямолинейный круглый стальной стержень ступенчато-переменного диаметра жестко защемлен одним концом и нагружен системой трех внешних крутящих моментов (рис. 3.2.11, а), причем М₁ = 2М; М₂ = 1,5М; М₃ = М, а М = 20 кНм.

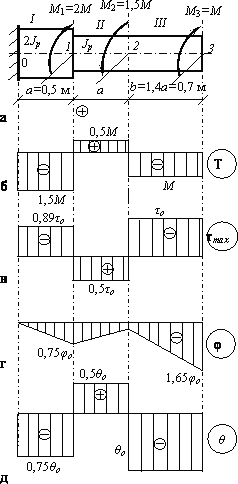
Построить эпюры крутящих моментов Т, абсолютных и относительныхуглов закручивания стержня, эпюру наибольших касательных напряженийв сечениях по всей длине стержня.

Из условий прочности и жесткости подобрать диаметры сплошного стержня для каждого участка, приняв в расчетах модуль сдвига G = 0,8·10⁵ МПа, расчетное сопротивление материала стержня (сталь) на срез R_s = 100 МПа, допускаемый относительный угол закручивания = 0,4 град/м. Полярные моменты инерции и длины участков показаны на рис.а.

Решение.

Обозначим цифрами характерные сечения на стержне. Имеем для II и III участков

(a)

где через d обозначен диаметр стержня в пределах этих участков. Для участка I получаем:

откуда находим (б)

Кроме того,

(в)

Определим внутренние крутящие моменты на каждом участке, начиная со свободного конца:

T_III = –M₃ = –M; T_II = –M₃ + M₂ = –M + 1,5M = 0,5M;

T_I = –M₃ + M₂ – M₁ = –M + 1,5M – 2M = –1,5M.

Строим эпюру крутящих моментов Т(рис.б).

Определяем наибольшие касательные напряжения на каждом участке, используя формулу

:

В последних формулах введено обозначение

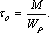(г)

Строим эпюру максимальных касательных напряжений по длине стержня (рис. в).

Определяем углы закручивания отдельных участков по формуле :

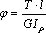где введено новое обозначение

(д)

Вычисляем углы поворота характерных сечений стержня:

По полученным результатам строим эпюру (рис.г).

Определяем относительные углы закручивания на каждом участке стержня по формуле :

Строим эпюру (рис.д).

По эпюре (рис. в) видно, что самое большое касательное напряжение будет на участкеIII, поэтому формулу записываем применительно к этому участку

По эпюре очевидно, что самый большой относительный угол закручивания будет на участкеIII, поэтому применяем формулу для участкаIII:

Сравнивая результаты расчетов на прочность (d = 0,1 м) и на жесткость (d = 0,14 м) находим, что главенствующим в рассматриваемой задаче является расчет на жесткость, посколькуd = 0,14 м > 0,1 м. Окончательно принимаемd = 14 см.

Определяем диаметры сечений остальных участков:

d_II = d_III = d =14 см,

d_I =1,19d = 16,7 см.

Определим значение угла закручивания на правом торце стержня (рис.а) в сечении 3. Из эпюры(рис.г) выписываем с учетом формул (д) и (а):

 

46