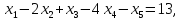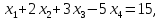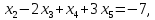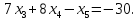- •Министерство образования и науки российской федерации
- •2013 Г. Содержание
- •Предисловие
- •Порядок выполнения и оформления лабораторных работ
- •Методические указания общего характера по применению средств программы "Wolfram Mathematica 7"
- •1. Списки и множества
- •Задания:
- •2. Числовые системы
- •Задания:
- •3. Алгебра многочленов
- •Задания:
- •4. Векторы и матрицы
- •Задания:
- •5. Уравнения и системы уравнений
- •Задания:
- •6. Функции действительных переменных
- •Задания:
- •Литература
Задания:
4.1. Даны
матрицы
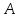 и
и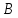 .
(Задать матрицы самостоятельно по
образцам с учетом указаний преподавателя.)
Требуется вычислить матрицы:
.
(Задать матрицы самостоятельно по
образцам с учетом указаний преподавателя.)
Требуется вычислить матрицы: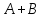 ;
;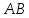 ;
;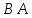 ;
;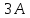 .
Образцы:
.
Образцы:
 ,
,
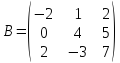
4.2. Требуется
выполнить умножение матриц
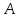 и
и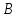 :
:
1) 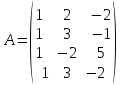 ,
,
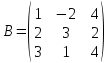 ;
;
2) 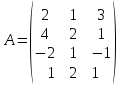 ,
,
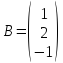 .
.
4.3. Требуется
вычислить определитель
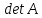 матрицы
матрицы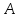 :
:
1) 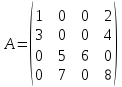 ;
2)
;
2) 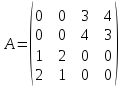 ;
;
3) 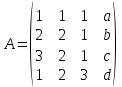 ;
4)
;
4) 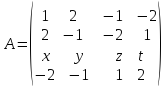 .
.
4.4. Требуется
вычислить обратной матрицы
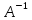 для данной матрицы
для данной матрицы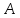 :
:
1) 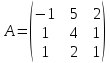 ;
2)
;
2) 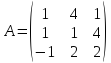 ;
3)
;
3) 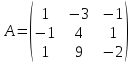 ;
;
4) 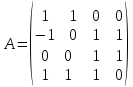 ;
5)
;
5) 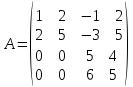 .
.
4.5. Даны
матрицы
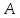 и
и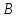 .
Требуется решить матричное уравнение
.
Требуется решить матричное уравнение .
.
1) 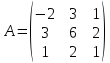 ,
,
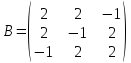 ;
;
2) 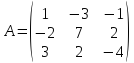 ,
,
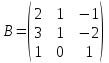 .
.
4.5. Требуется решить системы линейных уравнений:
1) 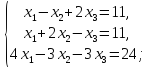 2)
2) 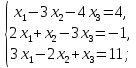
3) 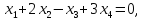
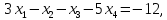
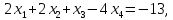
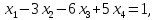
4) 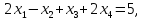
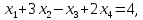
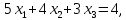
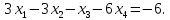
4.6. Пусть
даны векторы
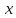 и
и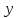 .
Требуется:
.
Требуется:
(a) найти
длины векторов
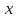 и
и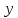 ;
;
(b) найти
угол межу векторами
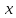 и
и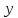 ;
;
(c) найти
проекцию
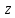 вектора
вектора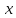 на вектор
на вектор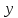 ;
;
(d) найти
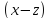 проверить, что
проверить, что .
.
1) 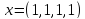 ,
,
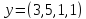 ;
;
2) 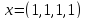 ,
,
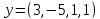 ;
;
3) 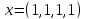 ,
,
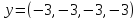 ;
;
4) 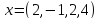 ,
,
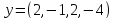 .
.
4.7. Пусть
даны векторы
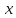 и
и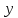 .
Рассмотреть треугольник, образованный
концами векторов
.
Рассмотреть треугольник, образованный
концами векторов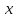 ,
,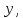
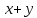 .
Требуется найти длины сторон и углы
треугольника, используя данные
упражнения 4.6.
.
Требуется найти длины сторон и углы
треугольника, используя данные
упражнения 4.6.
5. Уравнения и системы уравнений
Цель работы состоит в освоении технологий решения типовых задач по теме "Уравнения и системы уравнений".
Key words: Equal (==), Solve, Resolve, LinearSolve.
Возможные пути к ресурсам из окна Documentation Center:
1) Mathematics
and Algorithms
 Equation Solving.
Equation Solving.
2) ) Mathematics
and Algorithms
 Matrices and Linear Algebra
Matrices and Linear Algebra Linear Systems.
Linear Systems.
Пусть
имеется выражение
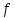 ,
содержащее незамещенную переменную
,
содержащее незамещенную переменную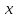 .
Запись вида
.
Запись вида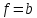 ,
где
,
где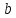 - известное значение, называютуравнением,
причем
- известное значение, называютуравнением,
причем
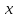 становитсянеизвестной
переменной. Значение
становитсянеизвестной
переменной. Значение
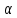 называютчастным
решением
уравнения, если при замещении
называютчастным
решением
уравнения, если при замещении
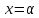 выполняется равенство
выполняется равенство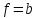 .Общее
решение
- это множество всех частных решений.
.Общее
решение
- это множество всех частных решений.
Если
же имеется некий список выражений
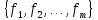 ,
содержащих незамещенные переменные из
списка
,
содержащих незамещенные переменные из
списка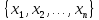 ,
то возникаетсистема
уравнений
как запись вида
,
то возникаетсистема
уравнений
как запись вида
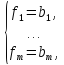
где
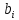 - известные значения, а
- известные значения, а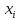 - неизвестные переменные. Список значений
- неизвестные переменные. Список значений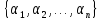 называютчастным
решением
системы уравнений, если при одновременном
замещении всех переменных (
называютчастным
решением
системы уравнений, если при одновременном
замещении всех переменных (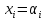 )
выполняются все равенства
)
выполняются все равенства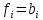 .Общее
решение
- это множество всех частных решений.
.Общее
решение
- это множество всех частных решений.
Если
есть отдельное уравнение или система
уравнений, то возникает задача о
нахождении общего решения. В системе
Mathematica
имеются т. н. решатели,
предназначенные для поиска общих решений
уравнений и систем уравнений. Во многих
случаях10применяют решательSolve.
Чтобы решить уравнение и систему
уравнений (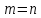 ),
можно написать:
),
можно написать:
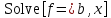
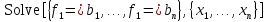
Всякая
запись вида
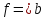 распознается программойWM7
как предикат
(неопределенное логическое выражение)
и, тем самым, может иметь имя.
распознается программойWM7
как предикат
(неопределенное логическое выражение)
и, тем самым, может иметь имя.
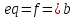 ;
;
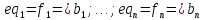 ;
;
то обращения к решателям могут быть представлены следующим образом:
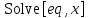
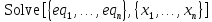
Задания:
5.1. Требуется решить уравнения:
1) 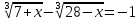 ;
2)
;
2) 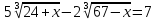 ;
;
3) 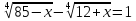 ;
4)
;
4) 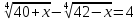 .
.
5.2. Требуется решить системы уравнений:
1) 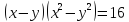 ,
,
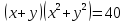 ;
;
2) 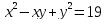 ,
,
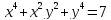 .
.
5.3. Требуется решить системы уравнений:
1) 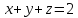 ,
,
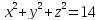 ,
,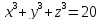 ;
;
2) 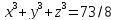 ,
,
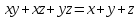 ,
,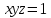 .
.
5.4. Требуется
найти значения параметра
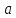 ,
при которых многочлены
,
при которых многочлены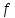 и
и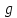 имеют общий корень. Найти соответствующие
общие корни.
имеют общий корень. Найти соответствующие
общие корни.
1) 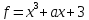 ,
,
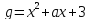 ;
;
2) 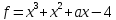 ,
,
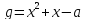 ;
;
3) 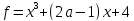 ,
,
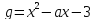 ;
;
4) 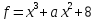 ,
,
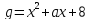 .
.
5.5. Требуется
найти значения параметра
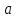 ,
при которых многочлен
,
при которых многочлен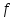 имеет кратный корень. Найти соответствующие
кратные корни (с указанием кратности).
имеет кратный корень. Найти соответствующие
кратные корни (с указанием кратности).
1) 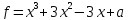 ;
2)
;
2) 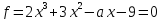 ;
;
3) 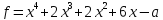 ;
;
4) 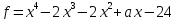 ;
;
5.6. Требуется
найти значения параметров
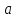 и
и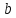 ,
при которых многочлен
,
при которых многочлен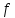 имеет кратный корень кратности
имеет кратный корень кратности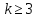 .
Найти соответствующие кратные корни
(с указанием кратности).
.
Найти соответствующие кратные корни
(с указанием кратности).
12) 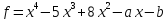 ;
;
13)  ;
;
14) 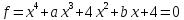 ;
;
15)  .
.
5.7. Требуется решить системы линейных уравнений:
1) 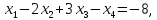
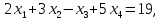
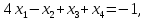
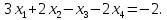
2)