- •Министерство образования и науки российской федерации
- •2013 Г. Содержание
- •Предисловие
- •Порядок выполнения и оформления лабораторных работ
- •Методические указания общего характера по применению средств программы "Wolfram Mathematica 7"
- •1. Списки и множества
- •Задания:
- •2. Числовые системы
- •Задания:
- •3. Алгебра многочленов
- •Задания:
- •4. Векторы и матрицы
- •Задания:
- •5. Уравнения и системы уравнений
- •Задания:
- •6. Функции действительных переменных
- •Задания:
- •Литература
Задания:
3.1. Для каждого выражения требуется:
(a) найти
коэффициенты при степенях
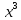 и
и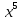 ;
;
(b) найти все коэффициенты единым списком;
(c) разложить
по степеням переменной 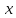 .
.
1) 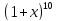 ;
2)
;
2) 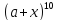 ;
3)
;
3) 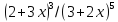 ;
;
4) 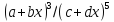 .
.
3.2. Требуется выполнить деление с остатком:
1) 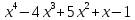 на
на
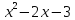 ;
;
2) 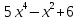 на
на
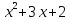 ;
;
3) 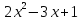 на
на
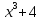 ;
;
4) 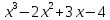 на
на
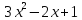 .
.
3.3. Требуется найти остаток при делении многочленов:
1) 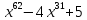 на
на
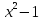 ;
;
2) 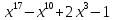 на
на
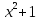 ;
;
3) 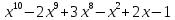 на
на
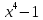 ;
;
4) 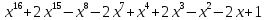 на
на
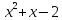 .
.
3.4. Требуется
выполнить деление многочлена
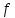 на линейный многочлен с остатком:
на линейный многочлен с остатком:
1) 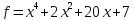 на
на
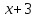 ;
;
2) 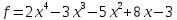 на
на
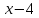 ;
;
3) 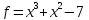 на
на
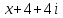 ;
;
4) 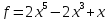 на
на
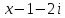 ;
;
5) 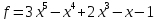 на
на
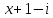 .
.
3.4. Требуется
вычислить значение многочлена
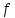 при
при
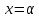 :
:
1) 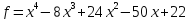 ,
,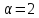 ;
;
2) 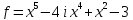 ,
,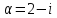 ;
;
3) 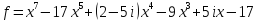 ,
,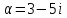 ;
;
4) 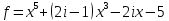 ,
,
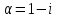 .
.
3.5. Требуется
разложить многочлены из задания 3.4
по степеням
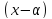 .
.
3.6. Требуется
определить кратность данного корня
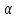 многочлена
многочлена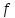 :
:
1) 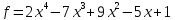 ,
,
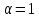 ;
;
2) 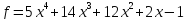 ,
,
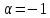 ;
;
3) 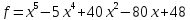 ,
,
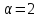 ;
;
4) 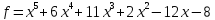 ,
,
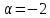 .
.
3.7. Требуется
найти кратные корни многочлена
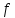 и определить
их кратности.
и определить
их кратности.
1) 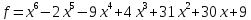 ;
;
2) 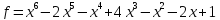 ;
;
3) 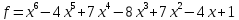 ;
;
4) 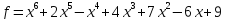 .
.
3.8. Для
каждого многочлена
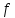 требуется:
требуется:
(a) выполнить тест на наличие кратных корней;
(b) предпринять попытку факторизации многочлена;
(c) предпринять поиск корней многочлена;
(c) составить отдельные множества действительных и комплексных корней.
1)  ;
2)
;
2) 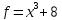 ;
3)
;
3) 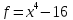 ;
4)
;
4) 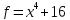 ;
;
5) 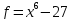 ;
6)
;
6) 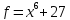 ;
7)
;
7) 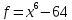 ;
8)
;
8) 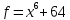 ;
;
9) 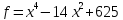 ;
10)
;
10) 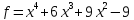 ;
;
11) 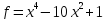 ;
12)
;
12) 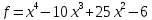 ;
;
13) 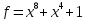 ;
14)
;
14) 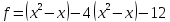 ;
;
15) 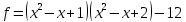 ;
;
16) 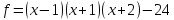 ;
;
17) 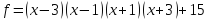 ;
;
18) 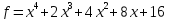 .
.
3.9. Требуется решить уравнения:
1) 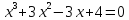 ;
2)
;
2) 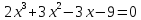 ;
;
3) 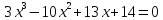 ;
4)
;
4) 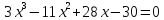 ;
;
5) 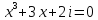 ;
6)
;
6) 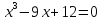 ;
;
7) 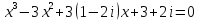 ;
;
8) 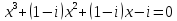 ;
;
9) 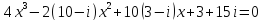 ;
;
10) 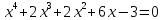 ;
;
11) 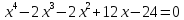 ;
;
12) 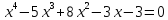 ;
;
13) 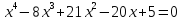 ;
;
14) 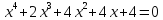 ;
;
15) 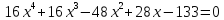 ;
;
16) 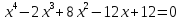 ;
;
3.10. Требуется факторизовать многочлены:
1) 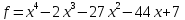 ;
;
2) 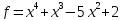 ;
;
3) 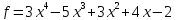 ;
;
4) 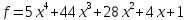 .
.
3.11. Требуется найти рациональные корни многочленов:
1) 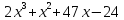 ;
;
2) 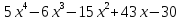 ;
;
3) 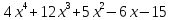 ;
;
4) 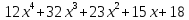 ;
;
5) 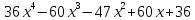 ;
;
6) 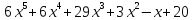 ;
;
7) 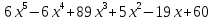 ;
;
8) 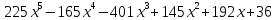 ;
;
9) 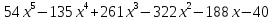 .
.
3.12. Требуется доказать, что следующие числа иррациональные:
1) 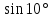 ;
2)
;
2) 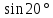 ;
3)
;
3) 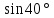 ;
4)
;
4) 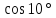 ;
5)
;
5) 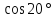 ;
;
6) 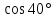 ;
7)
;
7) 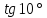 ;
8)
;
8) 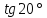 ;
9)
;
9) 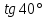 .
.
Указание. Используя формулы для тройного аргумента, сначала показать, что каждое из этих чисел является корнем кубического многочлена.
4. Векторы и матрицы
Цель работы состоит в освоении технологий решения типовых задач по теме "Векторы и матрицы".
Key words: Dot (.), Norm, VectorAngle, Projection, MatrixForm, IdentityMatrix, DiagonalMatrix, RotationMatrix, Inverse, Transpose, Det, Tr, Eigenvalues, Eigenvectors, Eigensystem, CharacteristicPolynomial.
Возможные пути к ресурсам из окна Documentation Center:
1) Mathematics
and Algorithms
 Matrices and Linear Algebra;
Matrices and Linear Algebra;
2) Notebooks
and Documents
 Mathematical Typesettings.
Mathematical Typesettings.
В
линейной алгебре всякий список, состоящий
из действительных чисел, рассматривается
как арифметический
вектор
(далее просто вектор),
причем длина списка служит размерностью
вектора. Векторы одной и той же длины
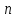 образуютарифметическое
векторное пространство
(действительное) размерности
образуютарифметическое
векторное пространство
(действительное) размерности
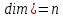 .
Общий вид вектора размерности
.
Общий вид вектора размерности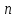 :
:
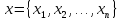 .
.
В каждом
арифметическом
векторном пространстве (ВП) фиксированной
размерности (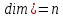 )
выполнимы линейные
операции:
сложение векторов и умножение вектора
на действительное
число (скаляр).
Эти операции являются частными случаями
общей формы:
)
выполнимы линейные
операции:
сложение векторов и умножение вектора
на действительное
число (скаляр).
Эти операции являются частными случаями
общей формы:
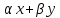 ,
,
где
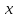 и
и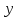 - векторы,
- векторы,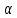 и
и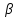 - скаляры. При этом нулевой список
- скаляры. При этом нулевой список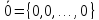 длины
длины
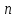 рассматривают
как нулевой
вектор.
рассматривают
как нулевой
вектор.
В арифметическом
ВП размерности
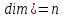 вводят стандартное скалярное
произведение
двух векторов:
вводят стандартное скалярное
произведение
двух векторов:
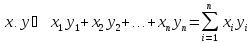 .
.
Арифметическое ВП со скалярным произведением рассматривается как евклидово ВП. В евклидовом ВП определяют норму вектора по формуле:
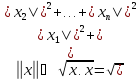 .
.
Справка. В аналитической
геометрии арифметические векторы
возникают естественным путем как списки
координат точек по отношению к системе
координат с началом 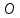 .
Всякая точка
.
Всякая точка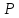 и еерадиус-вектор
и еерадиус-вектор
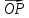 имеют единый список координат
имеют единый список координат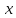 ,
так что
,
так что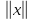 - этодлина
вектора
- этодлина
вектора
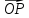 .
Если точки
.
Если точки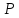 и
и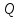 имеют координатные списки
имеют координатные списки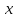 и
и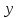 ,
тоевклидово
расстояние
между этими точками выражается формулой:
,
тоевклидово
расстояние
между этими точками выражается формулой:
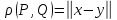 .
.
При работе с векторами в программе WM7 скалярное произведение (Dot) и норма вычисляются следующим образом:
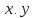
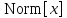
Тест
на ортогональность
векторов (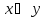 ):
):
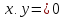
Угол
между векторами
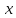 и
и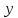 :
:
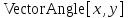
Проекция
вектора
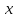 на вектор
на вектор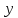 :
:
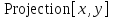
В ряде
разделов математики (и не только
в линейной алгебре) широко используются
матрицы. Всякая прямоугольная таблица
чисел (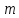 строк и
строк и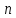 столбцов) рассматривается как числовая
матрица размера
столбцов) рассматривается как числовая
матрица размера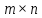 .
Общий вид матрицы размера
.
Общий вид матрицы размера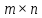 :
:
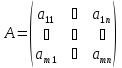 .
.
Матрицы одного и того же размера образуют некую алгебраическую систему (векторное пространство), в которой выполнимы линейные операции: сложение матриц и умножение матрицы на действительное число (скаляр). Эти операции являются частными случаями общей формы:
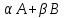 ,
,
где
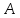 и
и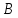 - матрицы,
- матрицы,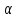 и
и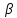 - скаляры. Как известно, существует
правило умножения матрицы
- скаляры. Как известно, существует
правило умножения матрицы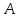 размера
размера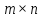 на матрицу
на матрицу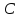 размера
размера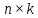 (справа).
При таком умножении получается матрица
(справа).
При таком умножении получается матрица
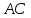 размера
размера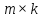 .
.
В системе
Mathematica
всякий матричный объект рассматривается
как список
списков:
1-ую позицию списка занимает список
элементов 1-ой строки, 2-ую позицию списка
занимает список элементов 2-ой строки,
и т. д. При желании можно рассматривать
матрицу размера
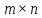 как список
как список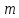 векторов размерности
векторов размерности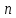 .
Ввод матрицы делается следующим образом:
.
Ввод матрицы делается следующим образом:
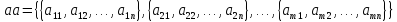
Чтобы
извлечь элемент
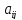 данной матрицы, можно написать:
данной матрицы, можно написать:
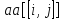
Умножение матриц выполняется с помощью функции Dot (.):
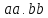
Наибольший
интерес представляют квадратные
матрицы (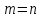 ).
Всеквадратные
матрицы одного и того же размера
).
Всеквадратные
матрицы одного и того же размера
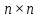 образуют более совершенную алгебраическую
систему (алгебру
матриц), в рамках которой выполнимы
следующие алгебраические операции:
линейные
операции
(сложение матриц и умножение матрицы
на действительное
число); умножение
матриц. Эти операции являются частными
случаями общей формы:
образуют более совершенную алгебраическую
систему (алгебру
матриц), в рамках которой выполнимы
следующие алгебраические операции:
линейные
операции
(сложение матриц и умножение матрицы
на действительное
число); умножение
матриц. Эти операции являются частными
случаями общей формы:
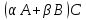 ,
,
где
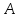 ,
,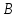 ,
,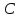 - квадратные матрицы размера
- квадратные матрицы размера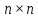 ,
,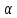 и
и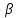 - скаляры. Особое положение в алгебре
матриц занимает единичная матрица
- скаляры. Особое положение в алгебре
матриц занимает единичная матрица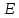 .
Далее, матрица
.
Далее, матрица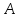 называетсяобратимой,
если существует обратная
матрица (обозначается через
называетсяобратимой,
если существует обратная
матрица (обозначается через
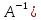 :
:
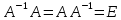 .
.
Вопрос
о существовании обратной матрицы
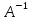 тесно связан с вычислениемопределителя
тесно связан с вычислениемопределителя
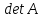 матрицы
матрицы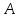 .
Если
.
Если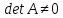 ,
то обратная матрица
,
то обратная матрица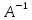 существует и может быть найдена известными
способами.
существует и может быть найдена известными
способами.
С использованием
обратной матрицы можно решать линейные
матричные уравнения, в том числе уравнения
вида
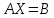 ,
где
,
где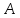 и
и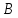 - заданные матрица, а
- заданные матрица, а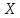 - неизвестная матрица. Искомое решение
может быть найдено по формуле:
- неизвестная матрица. Искомое решение
может быть найдено по формуле:
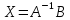 .
.
(В линейной алгебре этот подход известен как метод обратной матрицы.) В частности, всякая система линейных уравнений может быть записана в матричном виде.
Система Mathematica предоставляет широкий выбор средств для работы с квадратными матрицами. В частности, чтобы вычислить определитель матрицы и найти обратную матрицу, можно написать: