2. Кинетическая энергия точки и механической системы.

Кинетическая энергия материальной точки — скалярная положительная величина, равная половине произведения массы точки на квадрат ее скорости, т. е. .

Кинетическая энергия механической системы — арифме­тическая сумма кинетических энергий всех материальных точек этой системы

.

Кинетическая энергия системы, состоящей из п связанных между собой тел, равна арифметической сумме кинетических энергий всех тел этой системы:

.

Теорема Кенига. Кинетическая энергия механической системы в общем случае ее движения равна сумме кинетической энергии движения системы вместе с центром масс и кинетической энергии системы при ее движении относительно центра масс:

,

где — скоростьk - й точки системы относительно центра масс.

Поступательное движение.

При поступательном движении тела

.

Вращение тела вокруг неподвижной оси .

.

,

где - момент инерции тела относительно оси вращения.

Плоскопараллельное движение.

,

где — момент инерции плоской фигуры относительно оси, проходящей через центр масс.

Задача 1. Вычислить кинетическую энергию однородного диска массы М =10 кг, катящегося без скольжения со скоростью = 5м/с.

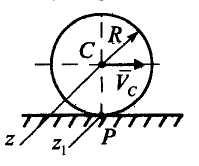
Решение. Диск совершает плоскопарал­лельное движение .

.

3. Теорема об изменении кинетической энергии точки

Теорема в дифференциальной форме. Дифференциал от кинетической энергии материальной точки равен элементарной работе силы, действующей на точку.

Доказательство:

.

Подставим в выражение второго закона динамики

;

.

Теорема интегральной (конечной) форме. Изменение кинетической энергии материальной точки на некотором перемещении равно работе силы, действующей на точку, на том же перемещении.

Доказательство

Дифференциал от кинетической энергии точки равен эле­ментарной работе:

.

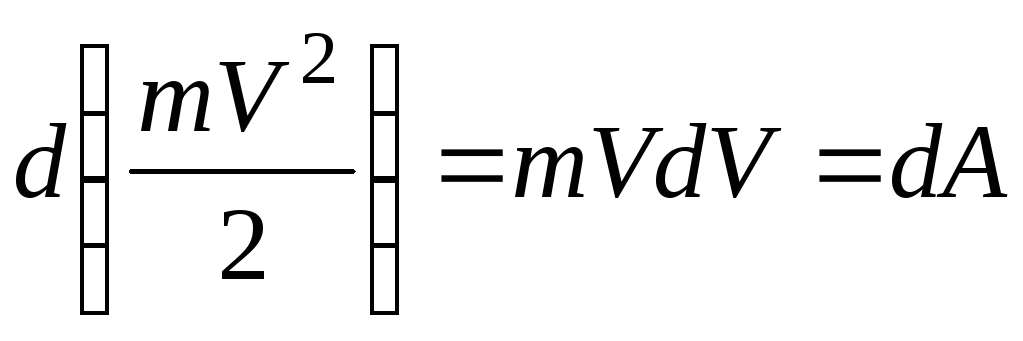Проинтегрируем

.

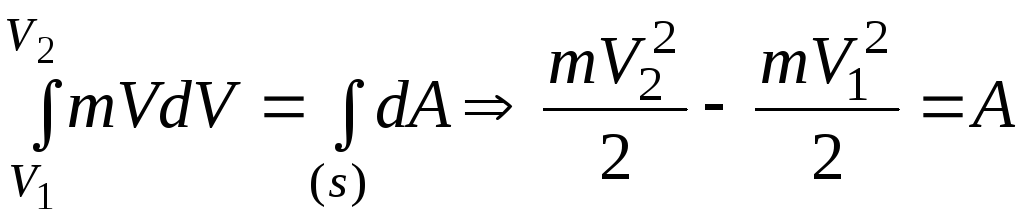4. Теорема об изменении кинетической энергии механической системы.

Теорема в дифференциальной форме. Дифференциал от кинетической энергии механической системы равен сумме элементарных работ внешних и внутренних сил, действующих на систему.

Доказательство: Для k - й точки системы

.

где исоответственно — элементарная работа внешней и внутренней сил, приложенных кk- й точке.

Для всей системы

.

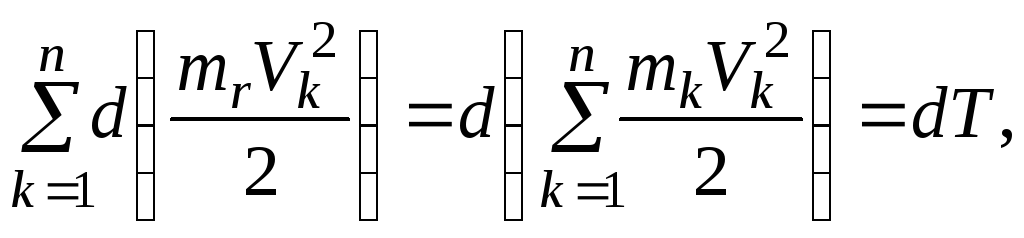
где — кинетическая энергия системы;— соответственно элементарная работа всех внешних и внутренних сил, приложенных к системе. Таким образом,

.

Для системы твердых тел

.

Тогда

.

Разделим на dt

,

где — мощность внешних сил;— мощность внутренних. Тогда

.

.

Теорема в интегральной (конечной) форме. Изменение кинетической энергии механической системы на некотором перемещении равно сумме работ внешних и внутренних сил, приложенных к системе, на том же перемещении.

Доказательство: Запишем теорему в интегральной форме для k- й точки системы:

,

где и— соответственно работа внешней и внутренней сил, приложенных кk-й точке, на некотором перемещении.

Суммируя по всем точкам системы, получим

Для системы твердых тел (по свойству внутренних сил). Тогда

.

Задача 2. Каток А приводится в движение из состояния покоя по­средством троса, который одним концом намотан на каток, а вто­рым — на барабан В. Каток А считать однородным цилиндром массы = 50кг и радиуса = 0,4м. Масса барабана = 20кг распределена по его ободу радиуса = 0,2м. К барабану при­ложен вращающий момент = 100Нм. Пренебрегая сколь­жением и трением качения катка по горизонтальной плоскости и весом троса, определить скорость катка, когда он переместится на расстояние s = 2 м.

Решение. Применим теорему об изменении кинетической энергии механической системы в интегральной форме:

,

где — система движется из состояния покоя

—по свойству внутренних сил. Тогда .. КатокА совершает плоскопараллельное движение.

.

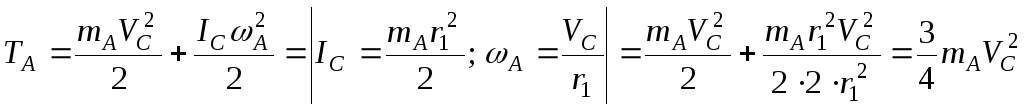Барабан В совершает вращательное движение.

.

.

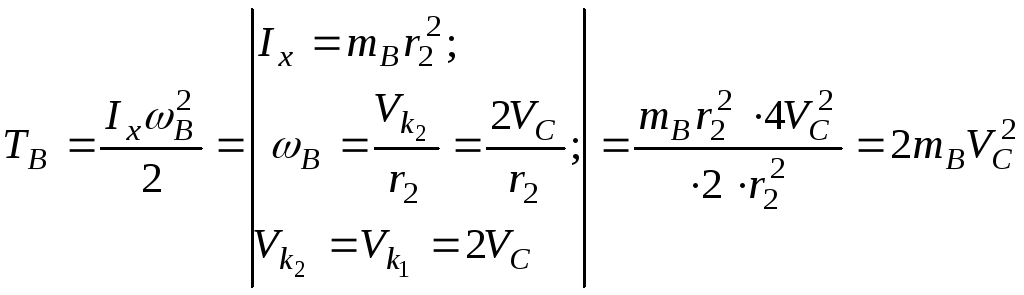Внешними силами являются силы тяжести , нормальная реакция, сила сцепления, вращающий мо­мент, реакциии.

так как сила ;так как силаприложена в МЦС;так как;,,— точка приложения сил не перемещается.

, где .

Тогда