
otveti na voprosi
.docБаскаков С. И. Электродинамика и распространение радиоволн 1992
1. Понятие комплексного числа (24)
2. Знать выражения операторов классической теории поля (Наббла, градиент, дивергенция, ротер и Лапласса) (25)
1. Ток смещения (1.7)
2. Поляризационные и сторонние токи (1.10)
3. Сводка уравнений Максвелла (2.1)
4. Уравнение Максвелла для гармонических колебаний. Комплексные амплитуды полей (2.2)
5. Комплексная диэлектрическая проницаемость. Угол диэлектрических потерь (2.3)
6. Энергетические соотношения в электромагнитном поле. Вектор Пойтинга (2.4)
7. Магнитный ток. Принцип перестановочной двойственности (2.5)
8. Лемма Лоренца (2.6)
9. Понятие волнового процесса. Продольные и поперечные волны (3.1)
10. Плоские волны и их характеристики (3.2)
11. Затухание волн в материальных средах. Коэффициент распространения (3.3)
12. Волновой характер переменного электромагнитного поля. Уравнение Гельмгольца (3.4)
13. Понятие характеристического сопротивления. Плотность потока мощности в плоской электромагнитной волне (3.5)
14. Плоские волны, распространяющиеся в произвольном направлении (3.8)
15. Волны в хорошо проходящей среде (5.1)
16. Плазма и ее электродинамические параметры (5.2)
17. Распространение электромагнитных волн в бесстолкновительной плазме (5.3)
18. Неоднородные уравнения Максвелла. Постановка задачи (13.1)
19. Векторный и скальный потенциалы электромагнитного поля (13.2)
20. Калибровка потенциалов. Неоднородное уравнение Гельмгольца (13.3)
21. Решение неоднородного уравнения Гельмгольца. Функция Гримма (13.4)
22. Элементарный электрический излучатель (13.5)
23. Структура поля элементарного электрического излучателя (13.6)
24. Комплексные числа
25. Основные дифференциальные операторы поля
26. Теоремы Гаусса-Остроградского и Стокса
Комплексная диэлектрическая проницаемость. Угол диэлектрических потерь
Свойства
диэлектрика на переменном токе удобно
рассматривать пользуясь понятием
комплексной диэлектрической проницаемости,
![]() действительная и мнимая части комплексной
диэлектрической проницаемости.
действительная и мнимая части комплексной
диэлектрической проницаемости.
![]()
Это комплексная величина, описывающая диэлектрическую проницаемость (действительная часть) и потери в диэлектрике (мнимая часть).
Мнимая
и действительная части комплексной
диэлектрической проницаемости связаны
между собой соотношением
![]() Мнимую часть комплексной диэлектрической
проницаемости называют коэффициентом
диэлектрических потерь.
Мнимую часть комплексной диэлектрической
проницаемости называют коэффициентом
диэлектрических потерь.
Введение понятия комплексной диэлектрической проницаемости среды позволяет не только использовать известные решения уравнений Максвелла, полученные для диэлектрических сред, в средах полупроводящих и проводящих, но и провести более строгую классификацию сред по проводимости.
Так как мнимая часть комплексной части диэлектрической проницаемости зависит от частоты, то понятие проводимости является относительным, то есть одна и та же среда на разных частота может проявлять себя различным образом.
![]()
Изображая комплексную диэлектрическую проницаемость в виде вектора на координатной плоскости, зависимость между мнимой и действительной частью можно показать с помощью угла дельта (угол диэлектрических потерь), или с помощью тангенса этого угла. Тангенс угла диэлектрических потерь характеризует соотношение амплитуд плотности тока проводимости к плотности тока смещения. Чем больше этот угол, тем значительней доля электромагнитной энергии, рассеиваемой в виде теплоты, при протекании токов проводимости.
Энергетические соотношения в электромагнитном поле. Вектор Пойтинга
Электромагнитное поле способно накапливать и переносить энергию. Законы движения энергии в эл-магнитном поле вытекают из уравнений Максвелла.
Вектор Пойнтинга (также вектор Умова — Пойнтинга) — вектор плотности потока энергии электромагнитного поля, одна из компонент тензора энергии-импульса электромагнитного поля.
Энергетические соотношения в переменном электромагнитном поле определяются теоремой Умова-Пойнтинга:
-div![]() =
E2
+
=
E2
+![]() ,
где
,
где
![]() =[
=[![]()
![]() ]
– вектор Пойнтинга.
]
– вектор Пойнтинга.
Мощность тепловых потерь P
P
=![]()
Интеграл
W=![]() представляет
собой запас энергии эл-магнитного поля
внутри объема V
в фиксированный момент времени.
представляет
собой запас энергии эл-магнитного поля
внутри объема V
в фиксированный момент времени.
Если
эл-магнитное поле изменяется во времени
гармонически, тогда
вводится комплексный вектор Пойнтинга
![]() =
=![]() ,
где
,
где
![]() – сопряжённый комплекс напряжённости
магнитного поля. Тогда
– сопряжённый комплекс напряжённости
магнитного поля. Тогда
-![]() =
P
+
jQ
=
=
P
+
jQ
=![]() +
2j
+
2j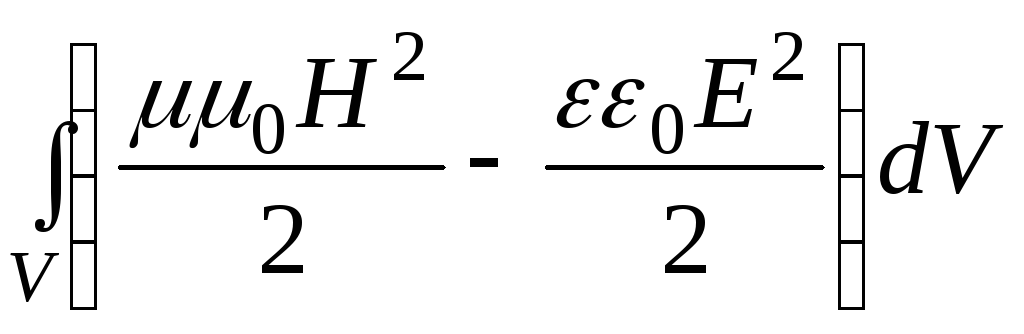 .
.
Интересный вывод: энергия переносится не токами в проводниках, а электромагнитным полем в окружающем пространстве.
Магнитный ток. Принцип перестановочной двойственности
Если электрические величины в уравнениях Максвелла заменить на магнитные, пользуясь следующим правилом:
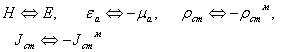
то первое уравнение Максвелла перейдет во второе, а второе соответственно в первое. Аналогично, третье уравнение Максвелла переходит в четвертое, а четвертое – в третье. Такая замена называется принципом перестановочной двойственности уравнений Максвелла.
В соответствии с этим принципом, если известно решение какой-либо электродинамической зада, простая перестановка позволяет сразу получить решение двойственной (дуальной) задачи, в которой конфигурация силовых линий магнитного поля повторяет конфигурацию силовых линий электрического поля в исходном процессе. При этом по сколько уравнения Максвелла не меняют своего вида, дуальный электромагнитный процесс заведомо существует.
(подробнее) http://thebard.narod.ru/PIVO/35PerestDvojstv.htm
Лемма Лоренца
Лемма Лоренца позволяет получить важные энергетические соотношения для электромагнитного поля. Она устанавливает взаимосвязь между разнесенными в пространстве сторонними источниками и возбуждаемыми ими электромагнитными полями.
(позволяет выразить электромагнитное поле внутри объема V через значения касательных составляющих векторов Е и Н на поверхности ( границе) области.)
Лемма Лоренца справедлива для неоднородных, изотропных сред. В случае неизотропной среды она неверна за исключением сред с симметричным тензором диэлектрической и магнитной проницаемости.
(подробнее) http://page-book.ru/i516527
http://lib.convdocs.org/docs/index-240149.html?page=5
